
通過算は中学受験でも出題される算数(数学)の問題ですが、SPIでも出題されます。
通過算には必ず覚えておくべき3つのパターン(トンネルの通過・すれ違い・追い越し)がありますが、就活生や転職活動中の社会人の中には忘れてしまっている人も多いでしょう。
※「【SPI】転職・中途採用の対策法や問題・通過率などをSPIマスターが完全解説」もぜひ参考にしてください。
本記事ではSPIを今までに100回以上も受検し、日本一SPIに詳しい私カズマがSPIで出題される通過算の解き方やコツなどについてわかりやすく解説していきます。
最後には通過算の練習問題もご用意しているので、SPIを受検予定の就活生や転職活動中の社会人はぜひ最後までご覧ください。
ちなみにですが、SPIにはたった3時間の勉強でSPIが通過してしまう勉強法があります。
これさえあれば限りなく少ない努力で内定に大きく近づきます。
これは私が100回以上ものSPI受検を通して生み出した、どの本にも載っていない超コスパの良い究極の勉強法です。
興味のある人はぜひ以下のボタンからその方法をチェックしてみてください。
通過算とは?SPIでの出題頻度・難易度は?
通過算とは電車や車がトンネルや鉄橋を通過するときの速さや時間などを求める問題です。
電車同士がすれ違うのにかかる時間を求めたり、電車がその他の電車を追い越すのにかかる時間を求めたりするケースもあります。
SPIの非言語(数学)では通過算が出題範囲に含まれていますが、通過算は小学校で学習する内容なので、解き方のパターンさえ頭に入れておけばそこまで難しくありません。難易度としてはかなり易しい方です。
※SPIの非言語(数学)を完全解説した記事もぜひ合わせてご覧ください。
SPIにおける通過算の出題頻度ですが、SPIを今までに100回以上受検してきた私の感覚からすると、WEBテスティングよりもテストセンターでの出題頻度が高いです。
WEBテスティングでは通過算はあまり出題されないので、WEBテスティングを受検予定の人はそこまで対策優先度は高くないでしょう。
※SPIのWEBテスティングとは何かについて完全解説した記事もぜひ参考にしてください。
テストセンターにおける通過算の出題頻度は中くらいです。
テストセンターの受検までに時間がない人は通過算の対策の優先を高める必要はありませんが、まだ時間がある人は必ず対策をしておきましょう。
※SPIのテストセンターとは何かについて解説した記事もぜひ合わせてご覧ください。
【SPI】通過算の解き方3パターンを例題で解説
通過算には
- トンネルの通過
- すれ違い
- 追い越し
の3パターンがあります。SPIの通過算で点数を稼ぐためには必ずこの3パターンを頭に入れておかなければなりません。
それぞれのパターンについて例題で解説していきます。
トンネルの通過
※問題によってはトンネルが鉄橋や橋に変わったりします。
【例題】
40m/秒で走行する長さ400mの電車が長さ1000mのトンネルを通過するのにかかる時間は何秒か求めよ。
【解答&解説】
問題文を絵にすると以下のようになります。

通過算では
- 電車の先頭車両の先端がトンネルの端に接触した瞬間=電車がトンネルに入り始めた瞬間
- 電車の最後尾車両の末端がトンネルの端と離れる瞬間=電車がトンネルを出た(通過した)瞬間
となります。
つまり、長さ400m電車が1000mのトンネルを通過した場合の走行距離は400+1000=1400[m]となります。
電車の速さは40m/秒なので、この電車が1400mを走行するのにかかる時間は1400÷40=35[秒]・・・(答)となります。
※時間=距離÷速さで求められるのでした。詳しくは「【SPI】速度算の練習問題18問!コツや解き方・公式・計算方法を完全解説!」をご覧ください。
通過算におけるトンネルの通過は以下を公式として覚えておきましょう。
電車がトンネルを通過するのにかかる時間=(電車の長さ+トンネルの長さ)÷(電車の速さ)
すれ違い
すれ違いは電車同士がすれ違うのにかかる時間を求める問題です。
【例題】
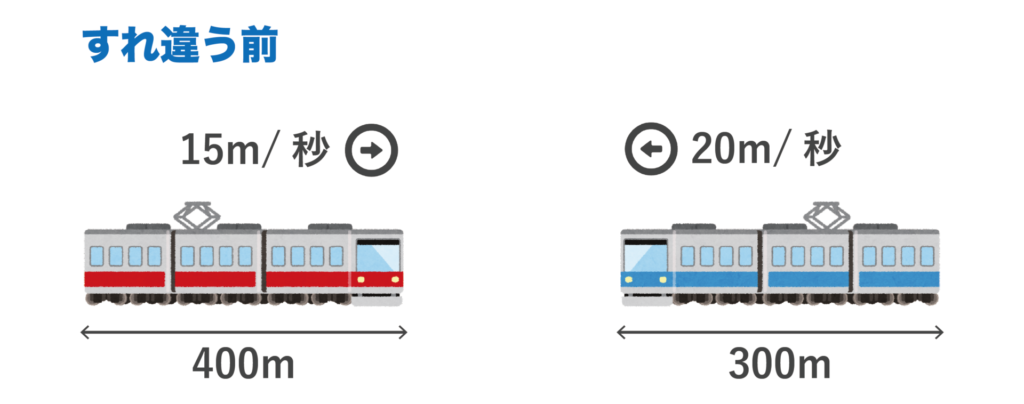
長さ400m・速さ15m/秒で走行する電車Aと長さ300m・速さ20m/秒で走行する電車Bが出会ってからすれ違うのに何秒かかるか求めよ。
【解答&解説】
電車Aと電車Bがすれ違う前の状況を絵にすると以下のようになります。
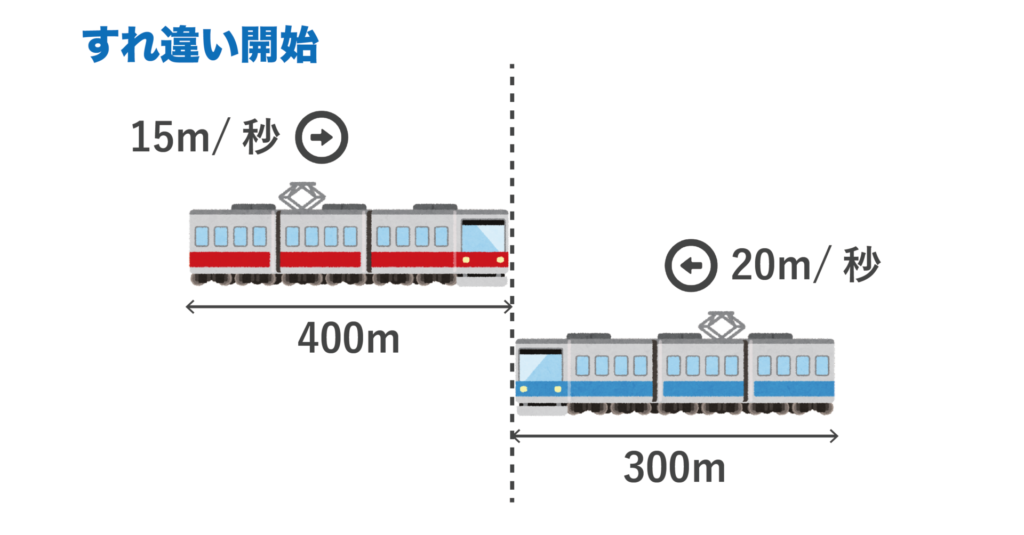
通過算では電車の先頭車両の先端同士が接触した瞬間=出会った瞬間(すれ違い開始)となります。
絵にすると以下のようになります。
そして、電車の最後尾車両の末端同士が離れる瞬間=すれ違い終了となります。
絵にすると以下のようになります。
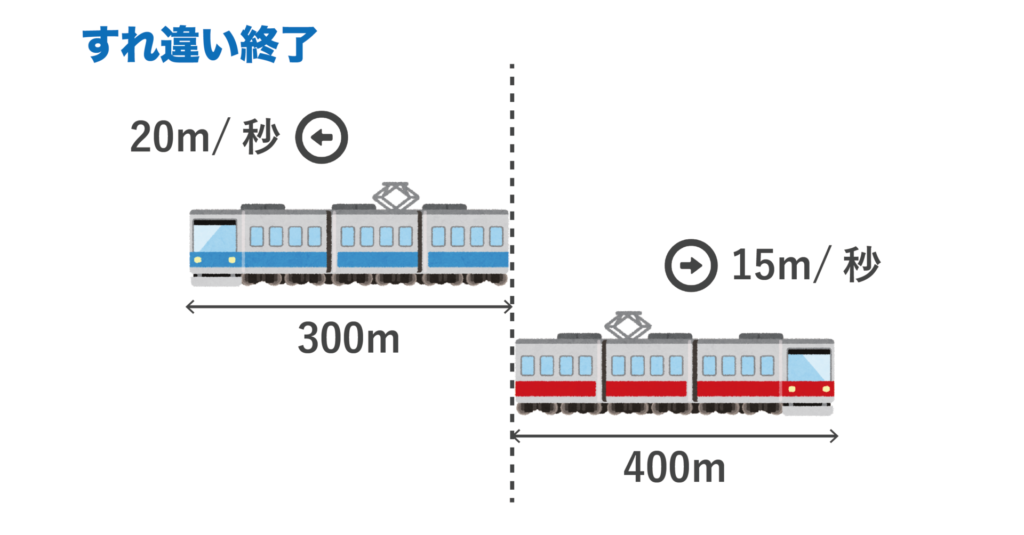
以上をもとにして考えると、電車Aと電車Bが移動した距離はともに400+300=700[m]であることがわかります。
そして、電車Aの速さは15m/秒、電車Bの速さは20m/秒なので、1秒間に35m(15+20より)ずつ距離が縮まっていきます。
よって求める答えは700÷35=20[秒]・・・(答)となります。
通過算におけるすれ違いは以下を公式として覚えておきましょう。
電車同士がすれ違うときにかかる時間=(電車の長さの合計)÷(速さの和)
追い越し
追い越しは電車が他の電車を追い越すのにかかる時間を求める問題です。
【例題】
長さ500m・速さ50m/秒で走行する電車Aが長さ400m・速さ20m/秒で走行する電車Bに追いついてから追い越すまでにかかる時間は何秒か求めよ。
【解答&解説】
電車Aが電車Bに追いつく前の状況を絵にすると以下のようになります。
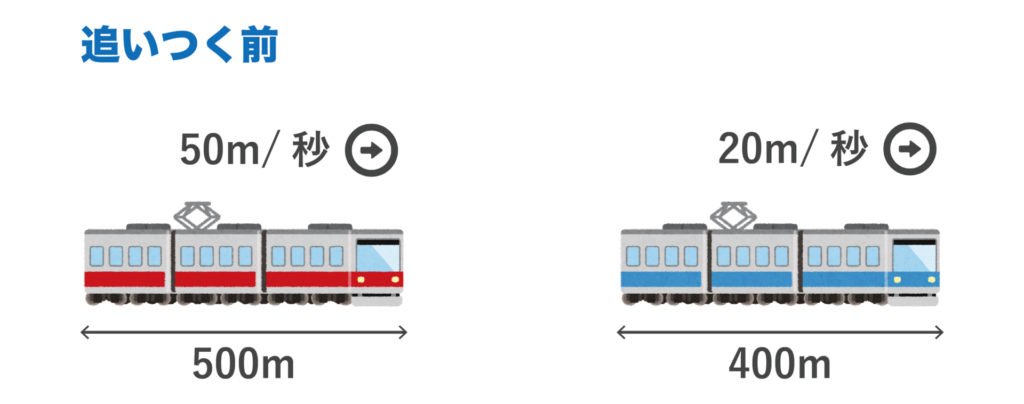
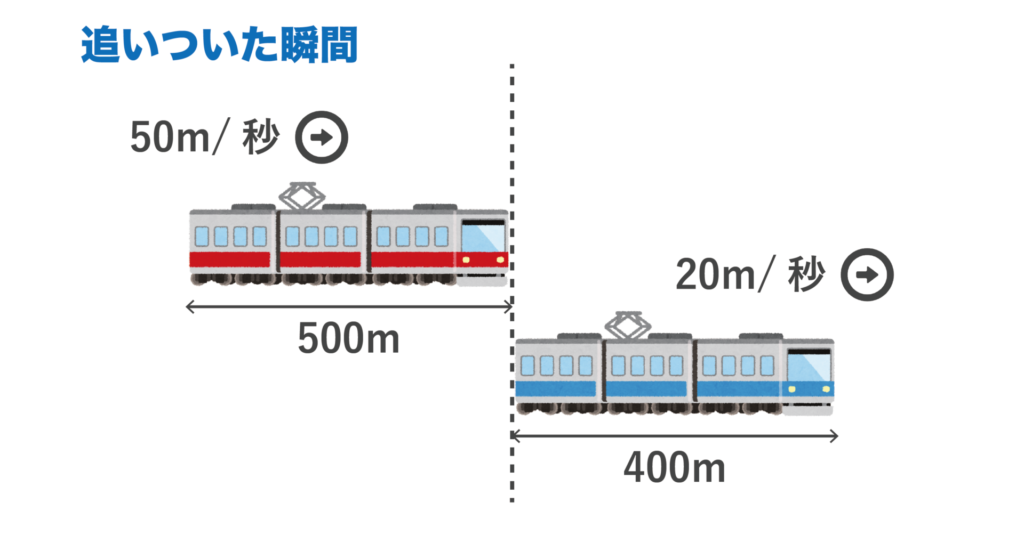
通過算では電車Aの先頭車両の先端が電車Bの最後尾車両の末端に接触した瞬間=追いついた瞬間となります。
絵にすると以下のようになります。
そして、電車Aの最後尾車両の末端が電車Bの先頭車両の先端から離れる瞬間=追い越した瞬間となります。
絵にすると以下のようになります。
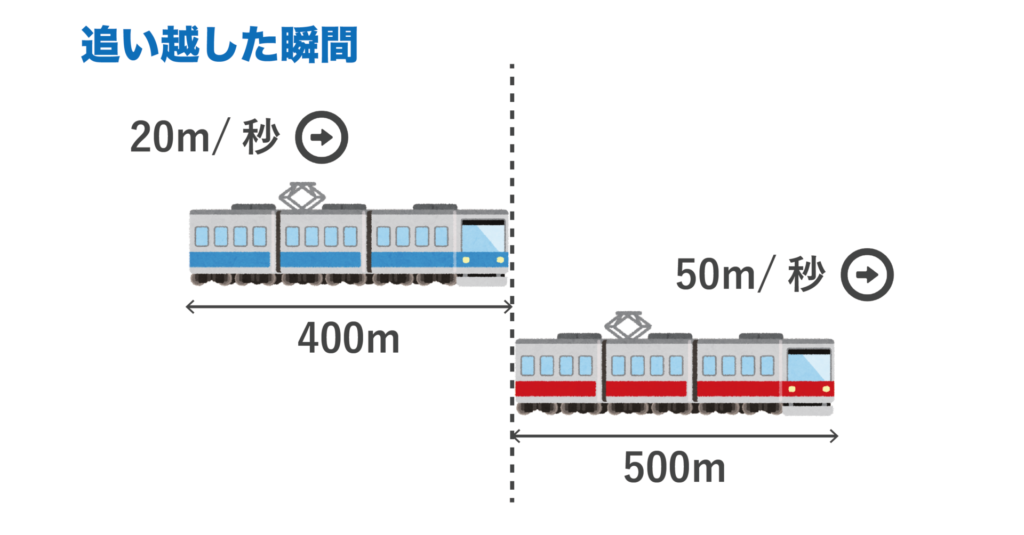
この場合も先ほど解説したすれ違いのパータンと同様に電車Aが移動した距離は2つの電車の長さの合計になるので、その距離は500+400=900[m]となります。
追い越しのパターンでは2つの電車が同じ方向に向かって走行しているので、1秒間に30m(50-20より)ずつ距離が縮まっていきます。
よって答えは900÷30=30[秒]・・・(答)となります。
通過算における追い越しは以下を公式として覚えておきましょう。
電車が他の電車を追い越すときにかかる時間=(電車の長さの合計)÷(速さの差)
以上が通過算で必ず覚えておくべき3つのパターンとなります。
【SPI】通過算の練習問題
最後にSPIで出題される問題の難易度に近い通過算の練習問題を5問ご用意しました。
テストセンター型のSPIを受検予定の人は特に解いておきましょう。
※SPIの練習問題をたくさん解きたい人はSPIの練習問題433問をすべて無料で掲載している記事もご用意しているので、ぜひご覧ください。
【練習問題】
(1)秒速30m、長さ130mの上りの急行列車が秒速20m、長さ120mの下りの普通列車と出会った。すれ違うのには何秒かかるか求めよ。
(2)24/秒で走る長さ240mの列車Pが、16m/秒で走る長さ160mの列車Qに追いついてから追い越すまでに何秒かかるか求めよ。
(3)長さ150mの電車が450mの鉄橋を通過するのに20秒かかった。この電車の速さは時速何kmか求めよ。
(4)25m/秒で走る長さ150mの列車が長さ2400mのトンネルに入った。このとき、トンネルの中に列車が完全に入っている時間は何秒か求めよ。
(5)ある電車が400mの鉄橋を通過するのに25秒かかり、840mのトンネルを通過するのに45秒かかる。この電車の速さは分速何mか求めよ。
(6)70km/時の列車Pが、74km/時で長さが130mの列車Qとすれ違いはじめてから、すれ違い終わるまでに7秒かかった。列車Pの長さは何mか求めよ。
【解答&解説】
(1)(130+120)÷(30+20)=250÷50=5[秒]・・・(答)
(2)(240+160)÷(24-16)=400÷8=50[秒]・・・(答)
(3)電車が進んだ距離は150+450=600[m]です。
よってこの電車の速さは600÷20=30[m/秒]です。
30[m/秒]=108000[m/秒]=108[km/時]・・・(答)となります。
(4)トンネルの中に列車が完全に入っている状況は絵にすると以下のようになります。
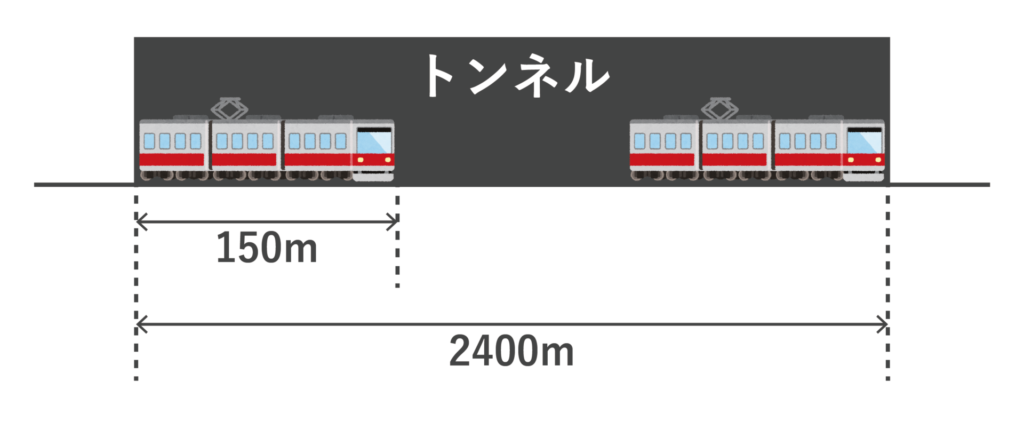
トンネルの中に入っている間に列車が進んだ距離は2400-150=2250[m]なので、答えは2250÷25=90[秒]・・・(答)となります。
(5)電車の速さをa[m/分]、電車の長さをb[m]とおきます。
すると、
- b+400=25a・・・(1)
- b+840=45a・・・(2)
という連立方程式を立てることができます。
(2)-(1)より20a=440となるので、a=22[m/秒]・・・(答)となります。
※連立方程式の解き方がわからない人は「【SPI】方程式はこの2つだけ絶対覚えよう!例題でわかりやすく解説!練習問題付き」をご覧ください。
(6)70+74=144[km/時]=40[m/秒]です。
列車Pの長さをa[m]とおくと、(a+130)÷40=7という一次方程式が立てられるので、a+130=280よりa=150[m]・・・(答)となります。
🔽 本にも載ってない極秘情報 🔽
今回はSPIの出題範囲に含まれている通過算について解説していきました。
本記事で解説した通り、通過算を解くには速度算の知識が必須です。速度算をまだ理解できていない人は速度算の学習から行いましょう。


