
SPIの非言語(数学)ではn進法に関する問題が出題されるという噂がありますが、それは完全な嘘なのでご注意ください(後ほど詳しく解説します)
SPIの受検予定者はn進法の対策をする必要はありません。
※「SPIの対策方法・勉強法を日本一SPIに詳しい筆者が真剣に考えてみた」もぜひ合わせてご覧ください。
本記事を執筆している筆者は今までにSPIを100回以上も受検していますが、SPIでn進法の問題が出題されたことは一度もありません。
今回はSPIとn進法の関係やSPIでn進法が出題されない理由などについて解説していきます。
SPIを受検予定の就活生や転職活動中の社会人はぜひ参考にしてください。
ちなみにですが、SPIにはたった3時間の勉強でSPIが通過してしまう勉強法があります。
これさえあればChatGPTなんて使う必要はありません。
これは私が100回以上ものSPI受検を通して生み出した、どの本にも載っていない超コスパの良い究極の勉強法です。
興味のある人はぜひ以下のボタンからその方法をチェックしてみてください。
目次
SPIでn進法は出題される?結論出題されません
本記事のタイトルでも結論を述べましたが、SPIの非言語(数学)ではn進法に関する問題は出題されません。
※SPIの非言語(数学)を完全解説した記事もぜひ参考にしてください。
念のためn進法とは何かについて解説しておきます。
n進法とはn個集まるごとに1つ上の位に進む位取りの仕組みのことです。
私たちが普段使用している数字は10の累乗ごとに位が
- 一の位(100)
- 十の位(101)
- 百の位(102)
- 千の位(103)
とあがっていくので、10進法と呼ばれています。
10進法は0、1、2、3、4、5、6、7、8、9の10個の数字で表現されます。
10進法があれば2進法や3進法、6進法など様々な進法(n進法)があります。
10進法を2進法に変換したり、2進法を3進法に変換したりすることも可能です。
n進法の問題としては以下のような問題があげられます。
【例題】
10進法の25を2進法で表しなさい。
※解答&解説は後ほどご紹介します。
SPIでn進法の問題が出題されない理由
SPIでは中学・高校で学習する内容をもとにして問題が出題されますが、本記事の読者の中には中学・高校でn進法を習った記憶がない人もいるでしょう。
本記事を執筆している筆者も中学・高校でn進法は習っていません。
n進法は従来は中学2年生の数学で学習する内容でしたが、平成14年度の学習指導要領の改訂によって学習項目から削除されてしまいました。
しかし、平成24年度の学習指導要領の改訂によってn進数は再び学習項目に追加され、n進数は高校の数学Aで学習することになりました。
以上の背景から、n進数を学習せずに中学・高校を卒業した人が多数いるため、SPIの非言語(数学)では出題範囲に含まれていないのです。
🔽 本にも載ってない極秘情報 🔽
10進法が日常生活でよく使われている理由
私たちに最も馴染みがあるのは10進法です。
私たちはお金を計算するときやお菓子の個数を数えるときなど、多くの場面で0~9の10個の数字を使って計算や表現をしています。
10進法が定着した理由は諸説ありますが、有力な説としては「人間の指が両手で10本あるから」があげられます。
人間は物を数えるために手の指を使うことがよくありますよね。
手の指で物を数えるときは10本の指を動かし終わったら、それを1つの単位と考え、10で一区切りとすることが多いでしょう。
昔の人も手の指で物を数えていたため、10進数が定着したと言われています。
ちなみにですが、私たちの日常生活では12進数・30進法・60進数もよく使われています。
例えば、1ダースは12個(本)です。つまり、12個(本)を1つのまとまりとして捉えます(12進数)
30進数は日付で使われています。1ヶ月=30日ですね(31日の月もありますが、ここでは一旦考慮しないものとします)
つまり、30日を1つのまとまりとして捉えているわけです。
60進数は時計で使われています。1分=60秒、1時間=60分です。
60秒または60分を1つのまとまりとして捉えています。

コンピューターでは2進法が使われている
ちなみにですが、コンピューターでは2進数が使われています。これは一般常識としても知っておきましょう。
コンピューターは電気信号を使って情報を処理するのですが、電気信号は「オン」と「オフ」の2つの値しか理解することができません。
10進数では0から9までの10個の数字を使うので、コンピューターが理解するのは難しいのです。
2進数は数字が0と1の2つの値だけを使うので、コンピューターと非常に相性が良いです。
電気信号を2進数で表現すれば情報を正確に伝えるのが簡単になるため、コンピューターは高速で計算を行うことが可能です。
2進数はコンピューターが情報を処理するための理想的な数の表現方法であると言えるのです。
10進数をn進数に変換する方法
SPIではn進数に関する問題は出題されませんが、せっかくの機会なのでn進数の変換方法について解説しておきます。
上記で「10進法の25を2進法で表しなさい」という例題をご紹介しましたが、これを解いてみます。
やり方は簡単です。10進数の数を以下のようにひたすら2で割っていくだけです。
最後の3÷2を行った時点で商の1が2よりも小さくなるので、ここでストップします。
そして、以下のように最後の商と余りに注目します。
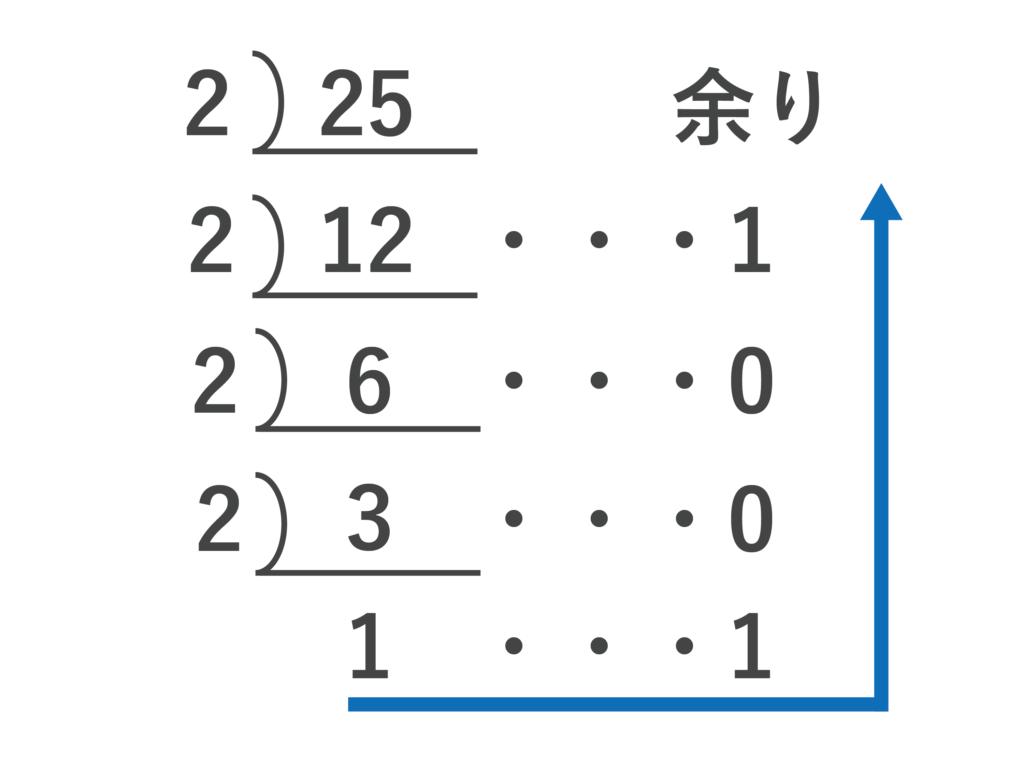
最後は商を先頭にして余りを上記矢印の順番に並べて、1101・・・(答)が答えとなります。
n進数を10進数に変換する方法
n進数を10進数に変換することももちろん可能です。
以下の例題を解いてみましょう。
【例題】
3進数の12012を10進数に変換せよ。
【解答&解説】
n進数を10進数に変換する場合、n進数で表された数の一の位はnの0乗を、十の位はnの1乗を、百の位はnの2乗を、千の位はnの3乗・・・を表します。
よって答えは、2×30+1×31+0×32+2×33+1×34=2+3+0+54+81=140・・・(答)となります。
※n0=1です。
n進数に関する練習問題
最後に、上記でご紹介した知識をもとにした練習問題をご用意しました。
SPIでは出題されませんが、興味のある人はぜひ解いてみてください。
【練習問題】
(1)10進法の71を3進法で表しなさい。
(2)10進法の592を4進法で表しなさい。
(3)10進法の321を6進法で表しなさい。
(4)10進法の1111を9進法で表しなさい。
(5)2進法の1011を10進法で表しなさい。
(6)4進法の1203を10進法で表しなさい。
【解答&解説】
(1)以下より、答えは2122となります。
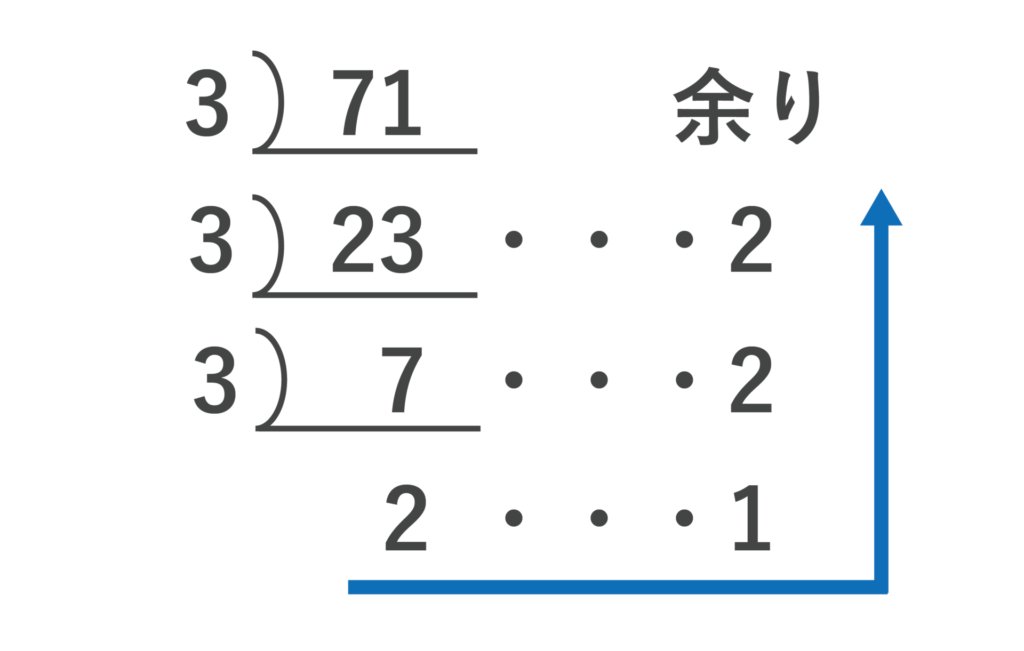
(2)以下より、答えは21100となります。
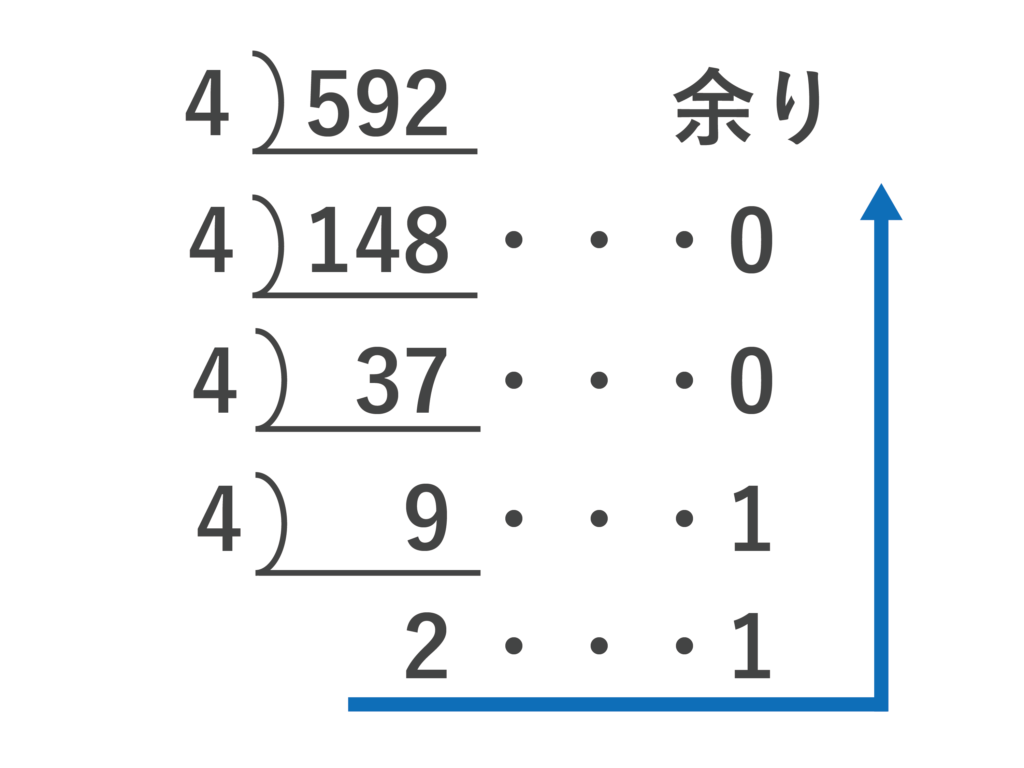
(3)以下より、答えは1253となります。
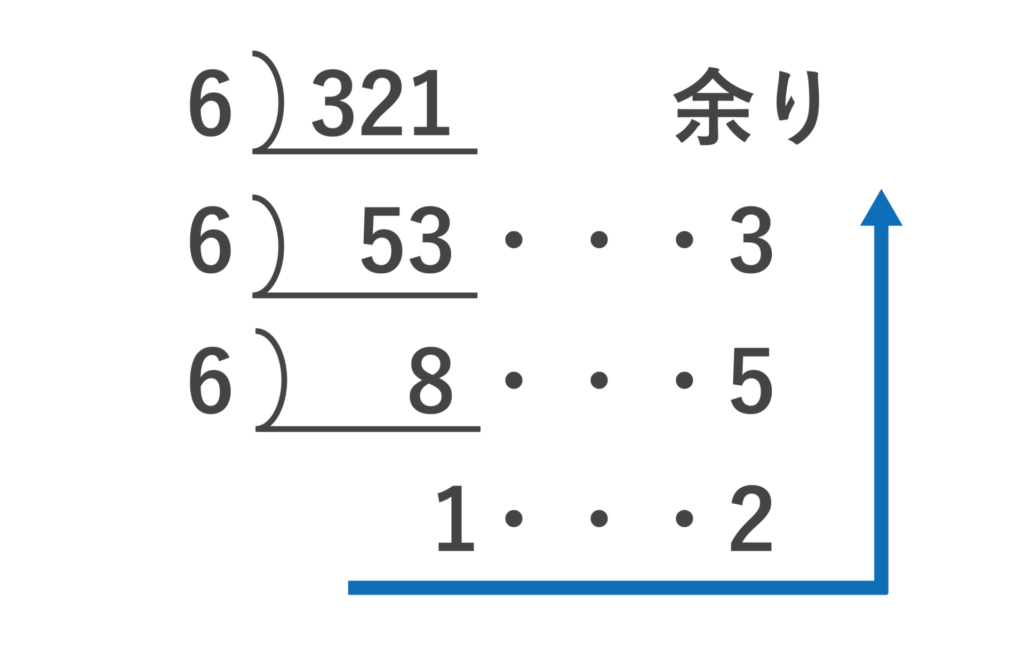
(4)以下より、答えは1464となります。

(5)1×20+1×21+0×22+1×23=1+2+0+8=11・・・(答)
(6)3×40+0×41+2×42+1×43=3+0+32+64=99・・・(答)
🔽 本にも載ってない極秘情報 🔽
今回はSPIでn進法は出題されるのか・n進法の問題の解き方について解説しました。
繰り返しにはなりますが、SPIではn進法の問題は出題されません。余力がある人は知識として持っておきましょう。


