
適性検査(WEBテスト)の1つであるSPIでは100人にアンケート問題が出題される可能性があります。
※「SPIとは?対策方法や問題・例題をすべて紹介!適性検査SPIはこれで完璧だ!」もぜひ合わせてご覧ください。
100人にアンケート問題は集合に関する問題で、難易度は中くらいです。
解き方のポイントの理解しておかないと解くことが難しい問題ので、必ず理解しておきましょう。
今回はSPIを今までに100回以上受検し、日本一SPIを熟知しているSPIマスターの私カズマが、SPIの非言語で出題される100人にアンケート問題の解き方やポイントについて図解で解説していきます。
ちなみにですが、SPIにはたった3時間の勉強でSPIが通過してしまう勉強法があります。
これさえあれば限りなく少ない努力で内定に大きく近づきます。
これは私が100回以上ものSPI受検を通して生み出した、どの本にも載っていない超コスパの良い究極の勉強法です。
興味のある人はぜひ以下のボタンからその方法をチェックしてみてください。
SPIの100人にアンケート問題とは?例題で解き方を解説
早速ではありますが、SPIの非言語で出題される100人にアンケート問題の例題をご紹介します。
※SPIの非言語(数学)を完全解説した記事もぜひ参考にしてください。
制限時間は1分30秒です。
【例題】
100人の主婦にアンケートを実施し、2つの商品AとBの知名度を調べた。その結果、Bを知っている人はAを知っている人の3倍で、どちらも知っている人は10人、どちらも知らない人は18人だった。このとき、Aだけを知っている人は何人か求めよ。
【解答&解説】
Aのみを知っている人の数をa人とおき、以下のようなベン図を描いてみます。
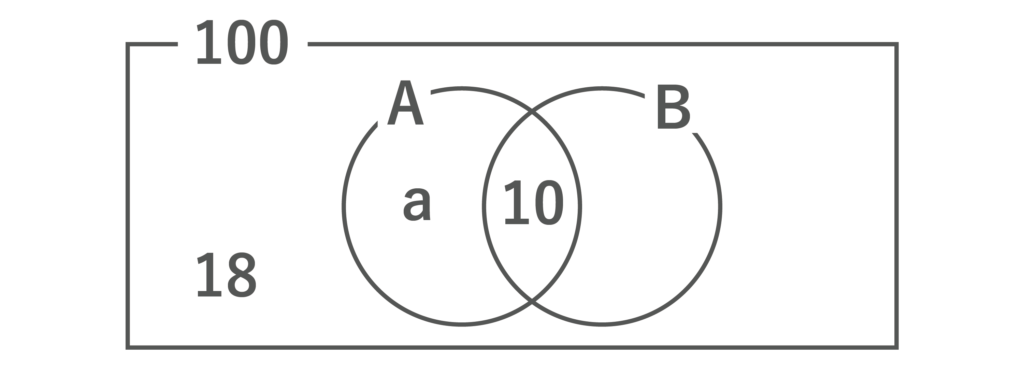
すると、Aを知っている人=(a+10)人であることがわかります。
問題文よりBを知っている人はAを知っている人の3倍なので、Bを知っている人=3(a+10)=(3a+30)人となります。
よって、以下のようなベン図を描くことができます。
※(3a+20)+10=3a+30になっています。
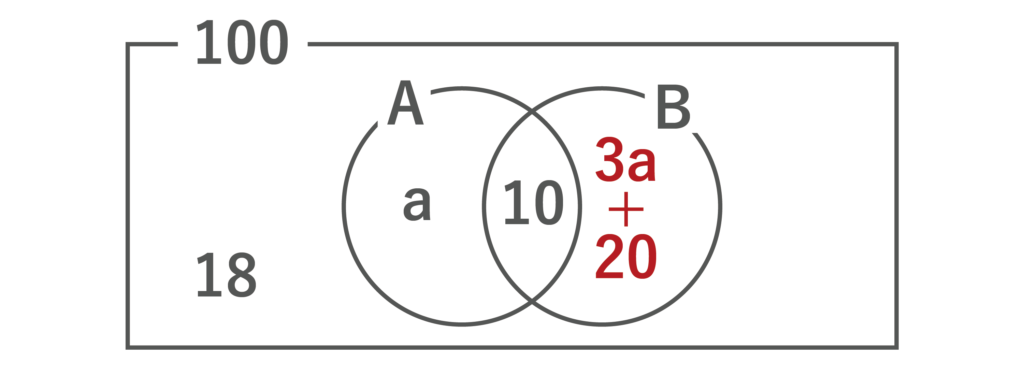
すると、a+10+(3a+20)+18=100という方程式が成り立つことがわかります。
この方程式を整理すると、4a+48=100より、4a=52となるので、a=13[人]・・・(答)が求まります。
※方程式の解き方がわからない人は「【SPI】方程式はこの2つだけ絶対覚えよう!例題でわかりやすく解説!練習問題付き」をご覧ください。
ちなみに、Bだけを知っている人は(3a+20)人なので、その人数は3×13+20=59[人]となります。
【別解】
ベン図ではなくカルノー表を使っても解くことができます。
※カルノー表の詳細については「SPIのカルノー表とは?具体例で使い方を解説!3つある場合は?」をご覧ください。
以下のようなカルノー表を作成してみます。
| 単位:[人] | Aを知っている | Aを知らない | 合計 |
|---|---|---|---|
| Bを知っている | 10 | A | 10+A |
| Bを知らない | B | 18 | 18+B |
| 合計 | 10+B | 18+A | 28+A+B |
すると、28+A+B=100より、A+B=72・・・(1)であることがわかります。
また、問題文よりBを知っている人はAを知っている人の3倍なので、10+A=3(10+B)が成り立ちます。
整理すると、A-3B=20・・・(2)です。
Aだけを知っている人は上記のカルノー表のBに該当するので、Bを求めていきます。
(1)-(2)より、4B=52となるので、B=13[人]・・・(答)です。
ちなみに、(1)より、A(Bだけを知っている人)=72-B=72-13=59[人]となります。
【SPI】100人にアンケート問題のポイント
100人にアンケート問題は集合問題の1つです。
集合問題はベン図またはカルノー表を使って解くことになりますが、カルノー表は3つ以上の集合が登場すると使えなくなるというデメリットがあります。
SPIの非言語では3つ以上の集合が登場するケースもあるので、基本的にはベン図を使って解くのがおすすめです。
ベン図が使えれば、カルノー表の使い方を無理に覚える必要はありません。
ベン図を使って集合問題を解くときのポイントはどの部分を文字にすればよいかを考えることです。
上記の例題ではAのみを知っている人の数をa人とおき、そこから方程式を立てていきました。
どの部分を文字にすればよいかわからない場合は一旦、テキトーな箇所を文字にしてみるのもアリです。
すると、そこから方程式を立てることができるケースも全然あります。
※基本的にはベン図における円の中の部分のどこかを文字にすることがほとんどです。
集合問題の解き方のコツなどをもっと知りた人は「【SPI】集合・ベン図の練習問題13選!解き方や3つ・少なくとものケースまで網羅」をご覧ください。
練習問題
最後に、上記でご紹介した100人にアンケート問題の難易度に近い集合の練習問題をご用意しました。
※SPIの練習問題433問をすべて無料で掲載している記事もぜひ参考にしてください。
こちらも解答・解説に図解を載せているので、ぜひ解いてみてください。
【練習問題1】
あるレストランではコーヒーを注文した客175人のうち、ミルクを入れた人は52%、砂糖を入れた人は36%、どちらも入れなかった人は28%だった。このとき、ミルクと砂糖の両方を入れた人の数を求めよ。
【解答&解説】
人数と%が混在しているので、どちらかにそろえます。
計算が速いのは175人を100%とするほうです。
客は「ミルクを入れた」「砂糖を入れた」「どちらも入れなかった」のいずれかに該当します。
3つを足して、100%を超えた分が両方入れた人になります。

52+36+28=116[%]より、116-100=16[%]が超過分(=両方入れた人の割合)です。
よって、答えは175×0.16=28[人]・・・(答)となります。
【練習問題2】
ある鳥取県の町の世帯数は80世帯で、猫を飼っている世帯は34世帯、犬を飼っている世帯は27世帯である。どちらか片方だけ飼っている世帯が49世帯のとき、どちらも飼っていない世帯は何世帯か求めよ。
【解答&解説】
両方飼っている世帯数を求め、全世帯80から「どちらか片方だけ飼っている世帯数」と「両方飼っている世帯数」を引きます。
両方飼っている世帯数は(34+27-49)÷2=6[世帯]です。
÷2をしている理由ですが、以下の図からわかるように、両方飼っている世帯は猫側と犬側との両方から数えられている部分だからです。
2で割ることでダブって数えられている分を取り除きます。
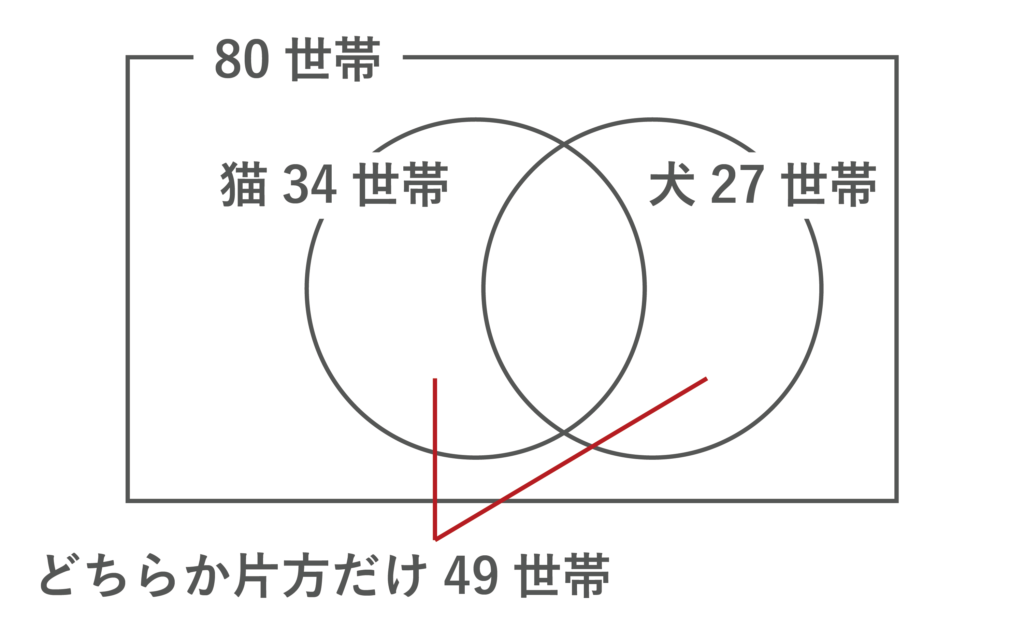
よって、答えは80-49-6=25[世帯]・・・(答)となります。
🔽 本にも載ってない極秘情報 🔽
今回はSPIの100人にアンケート問題を取り上げました。
繰り返しにはなりますが、SPIを受検予定の人はカルノー表よりもベン図も使えるようにしておきましょう。


