
SPIの非言語(数学・計数)では集合・ベン図に関する問題が出題範囲に含まれています。
※「SPIとは?対策方法や問題・例題をすべて紹介!適性検査SPIはこれで完璧だ!」もぜひ合わせてご覧ください。
しかし、集合・ベン図問題は苦手とする人が多く、難易度も少し高いのが特徴です。
就活生や転職活動中の社会人の中にはベン図の書き方を忘れてしまった人もいるでしょう。
※「【SPI】転職・中途採用の対策法や問題・通過率などをSPIマスターが完全解説」もぜひ参考にしてください。
そこで今回は日本一SPIについて詳しいSPIマスターの私カズマがSPIの集合・ベン図問題の解き方を例題でわかりやすく解説していきます。
解き方のコツや練習問題もご用意していますので、SPIを受検予定で数学が苦手な就活生や転職活動中の社会人はぜひ最後までご覧ください。
※「SPIの非言語(数学)を完全解説!対策方法やできない人でも点数を上げる方法!問題もご紹介」もぜひ合わせてご覧ください。
ちなみにですが、SPIにはたった3時間の勉強でSPIが通過してしまう勉強法があります。
これさえあれば限りなく少ない努力で内定に大きく近づきます。
これは私が100回以上ものSPI受検を通して生み出した、どの本にも載っていない超コスパの良い究極の勉強法です。
興味のある人はぜひ以下のボタンからその方法をチェックしてみてください。
SPIの集合・ベン図問題とは?解き方は?例題でわかりやすく解説
SPIで出題される集合・ベン図問題とはその名の通り、集合(=何かしらの条件によってグループ分けされたものの集まり)に関する問題です。
集合問題では以下のような図(ベン図といいます)を使って解くのが一般的なので、ベン図問題とも言われています。
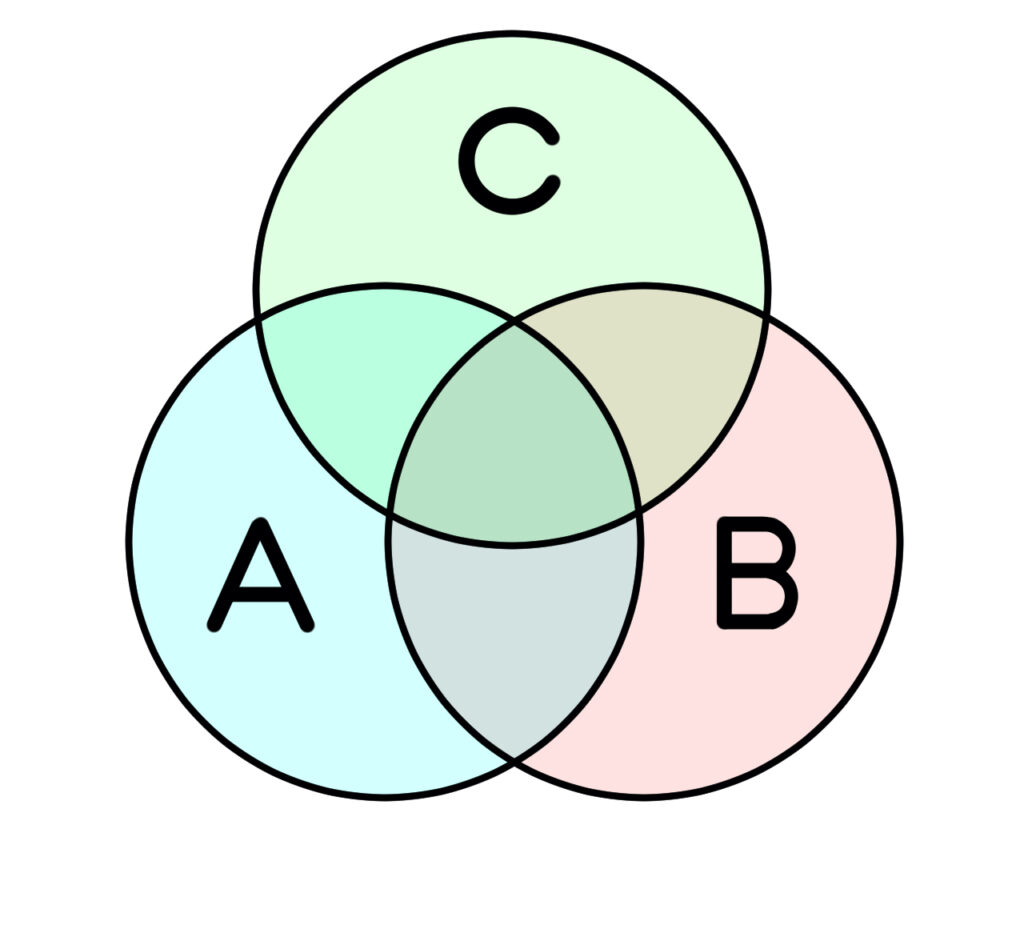
具体的には以下のような問題が出題されます。
【例題】
小学生に好きなお菓子に関するアンケートを取ったところ、チョコが好きと答えた小学生は120人、クッキーが好きと答えた小学生は40人だった。
また、チョコとクッキーの両方が好きと答えた小学生は30人だった。このとき、チョコとクッキーのどちらかだけ好きと答えた小学生は何人いたか求めよ。
【解答&解説】
以下のようなベン図を書いて解いていきます。今回、チョコとクッキーの両方が好きと答えた小学生は30人だったとのことなので、チョコの円とクッキーの円が重なる部分が30人になります。
そして、チョコの円から30人を引いた部分をA、クッキーの円から30人を引いた部分をBとしてみます。
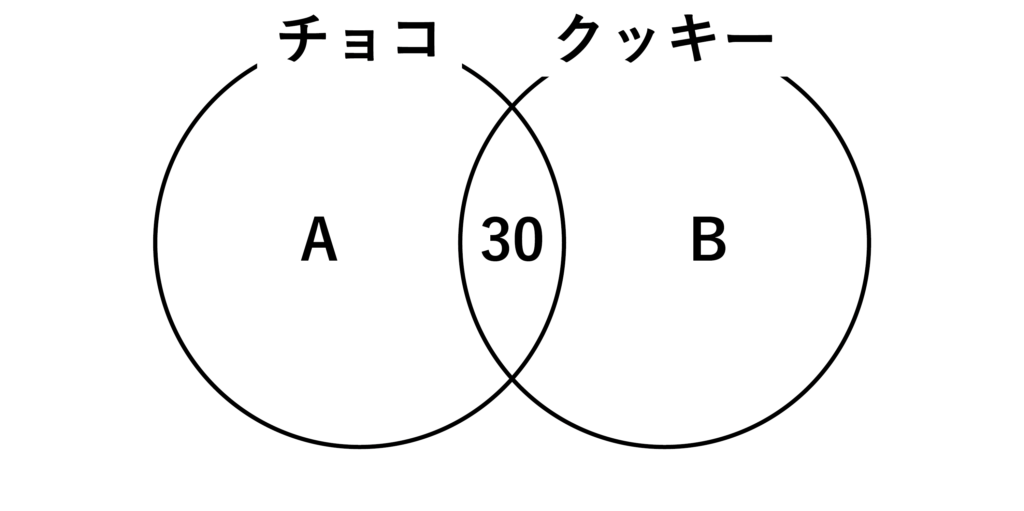
すると、チョコが好きと答えた小学生(=チョコの円の部分)は120人だったとのことなので、A+30=120が成り立ちます。よってA=90[人]・・・(答)となります。
同様に考えて、クッキーが好きと答えた小学生は40人だったとのことなので、B+30=40よりB=10[人]・・・(答)となります。
以上は集合の問題の中でも非常に基本的な問題です。SPIではもう少し難しい問題が出題されます(この後の練習問題でご紹介します)ので、この問題は必ず解けるようにしておきましょう。
※「【SPI】集合・ベン図の練習問題10選!図解の解答・解説付き」もぜひ合わせてご覧ください。
🔽 本にも載ってない極秘情報 🔽
SPIの集合・ベン図問題を解くコツ
先ほどの例題では2つの集合(円)が登場しましたが、SPIでは3つの円が登場するケースもあります。
SPIの集合・ベン図問題を解くコツは3つの円において、どの部分が何を指しているか?を暗記しておくことです。
例えば、問題文に
- チョコが好きな人
- クッキーが好きな人
- ケーキが好きな人
という3つの情報があった場合、3つの円(ベン図)を書くと以下7つの領域ができますね。
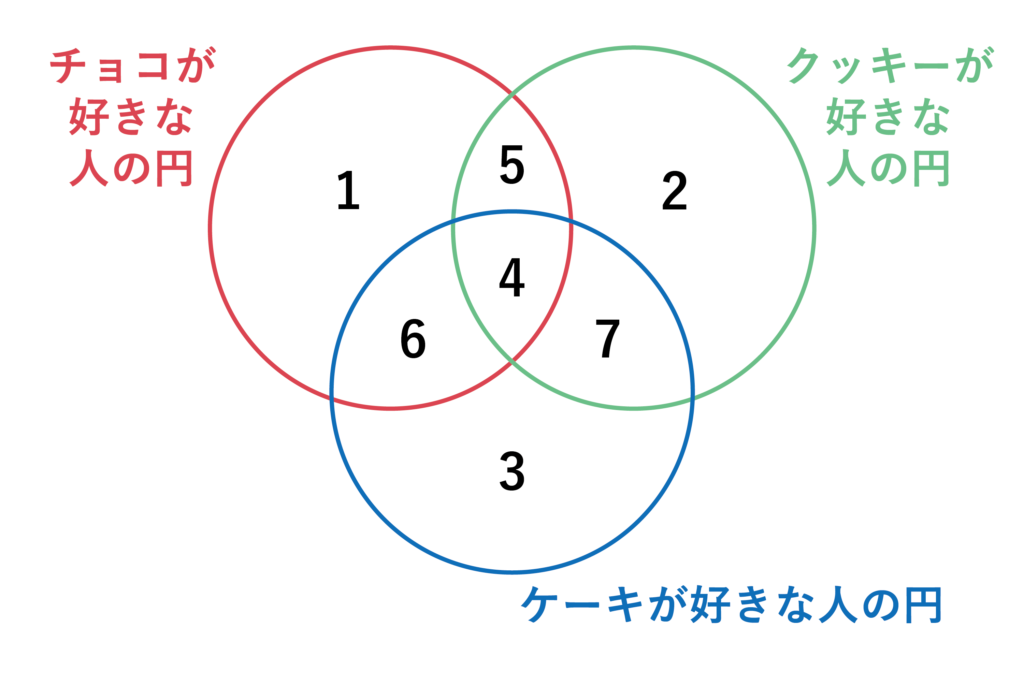
この7つの領域はそれぞれ以下を指しています。
- チョコだけ好きな人
- クッキーだけ好きな人
- ケーキだけ好きな人
- チョコ、クッキー、ケーキ全部好きな人
- チョコとクッキーが好きな人
- チョコとケーキが好きな人
- クッキーとケーキが好きな人
SPIを受検予定の人は以上を必ず覚えておきましょう。これを知っておくだけで集合・ベン図問題の計算がかなりしやすくなります。
SPIの集合・ベン図問題が出題される受検方式と難易度
SPIにはWEBテスティング、テストセンター、インハウスCBT、ペーパーテストという4つの受検方式がありますが、集合・ベン図問題はすべての受検方式で出題される可能性があります。
特にWEBテスティングでは最後の方の問題で出題されるケースが多いです。
※SPIのWEBテスティングを完全解説した記事もぜひ合わせてご覧ください。
SPIで出題される集合・ベン図問題の難易度は中〜難です。
※「SPIは難しい?難しすぎる?難易度を言語と非言語別に徹底解説してみた」もぜひ参考にしてください。
先ほども解説した通り、3つの円が登場するケースもあり、割と簡単に解ける問題もあれば少し工夫が必要な問題もあります。なので、集合・ベン図問題の勉強・対策の優先度は下げて問題ないでしょう。
SPIにおいて優先的に勉強・対策すべきは出題頻度が高いかつ難易度が易しい分野です。例としては速度算や損益算があげられます。
SPIの速度算の解き方について解説した記事やSPIの損益算について解説した記事もご用意しているので、ぜひ参考にしてください。
【SPI】集合・ベン図の練習問題
最後に集合・ベン図の練習問題をご用意しました。SPIで出題される問題の難易度に近い問題をご用意したので、非言語(数学・計数)で高得点を狙っている人はぜひ解いてみてください。
※SPIの高得点目安・指標について詳しく解説した記事もぜひ参考にしてください。
【練習問題1】
風邪を予防するために手洗いとマスクをしているかについて150人にアンケートをとったところ、マスクのみと答えた人は27人であることがわかった。
また、手洗いをしていると答えた人はどちらもしていないと回答した人よりも57人多く、手洗いもマスクも両方していると回答した人は54人であった。
このとき、手洗いのみしていると回答した人は何人か求めよ。
【解答&解説】
手洗いもマスクもどちらもしていない人=a[人]とおいてみます。すると、問題文より手洗いをしている人=a+57[人]となりますね。
また、手洗いもマスクも両方していると回答した人は54人とのことなので、以上3つの情報をベン図にしてみると以下のようになりますね。
※長方形の枠内かつ2つの円の外側=手洗いもマスクもどちらもしていない人=a[人]となります。
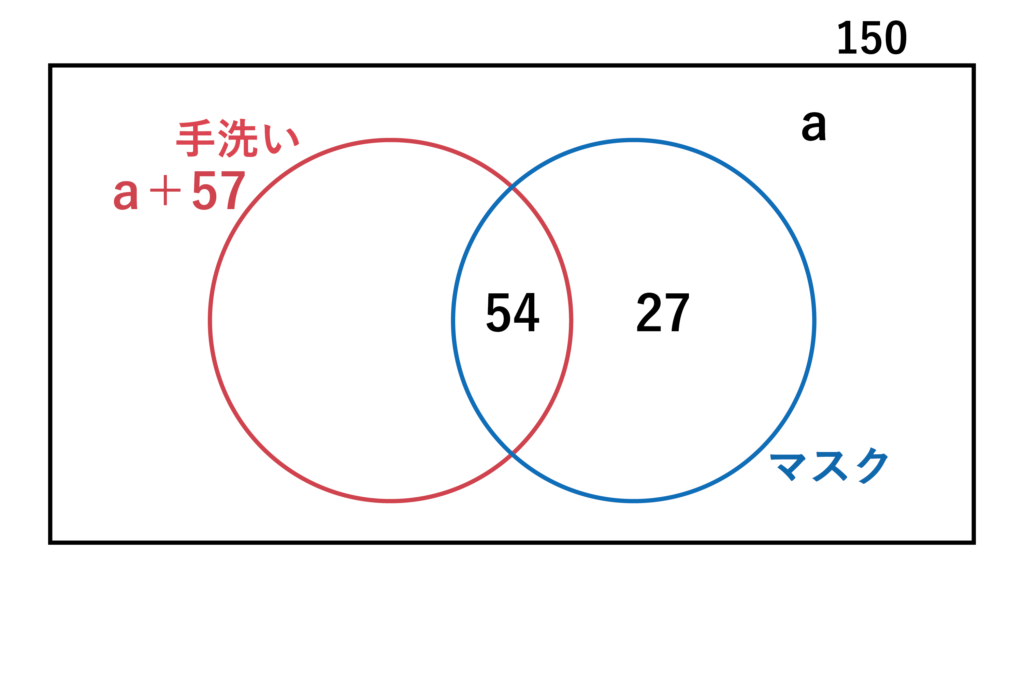
すると、(a+57)+27+a=150という方程式が立てられるので、2a+84=150より2a=66となるので、a=33であることがわかります。
※方程式の解き方がわからない人は【SPI】方程式はこの2つだけ絶対覚えよう!をご覧ください。
手洗いのみしていると回答した人=(a+57)-54なので、a=33を代入して、(33+57)-54=36[人]・・・(答)となります。
【練習問題2】
スポーツの好みについて200人にアンケートをとった。サッカーが好きな人は全体の65%で、そのうちの40%は野球も好きであった。また、野球・サッカーのいずれも好きではない人は18人いた。このとき、野球が好きな人は何人か求めよ。
【解答&解説】
問題文より、サッカーが好きな人=200×65%=200×0.65=130[人]であることがわかります。
そのうち40%は野球も好きとのことなので、その人数=130×40%=52[人]となります。
以上の情報をベン図にすると、以下のようになりますね(野球だけが好きな人=a[人]とおいています)
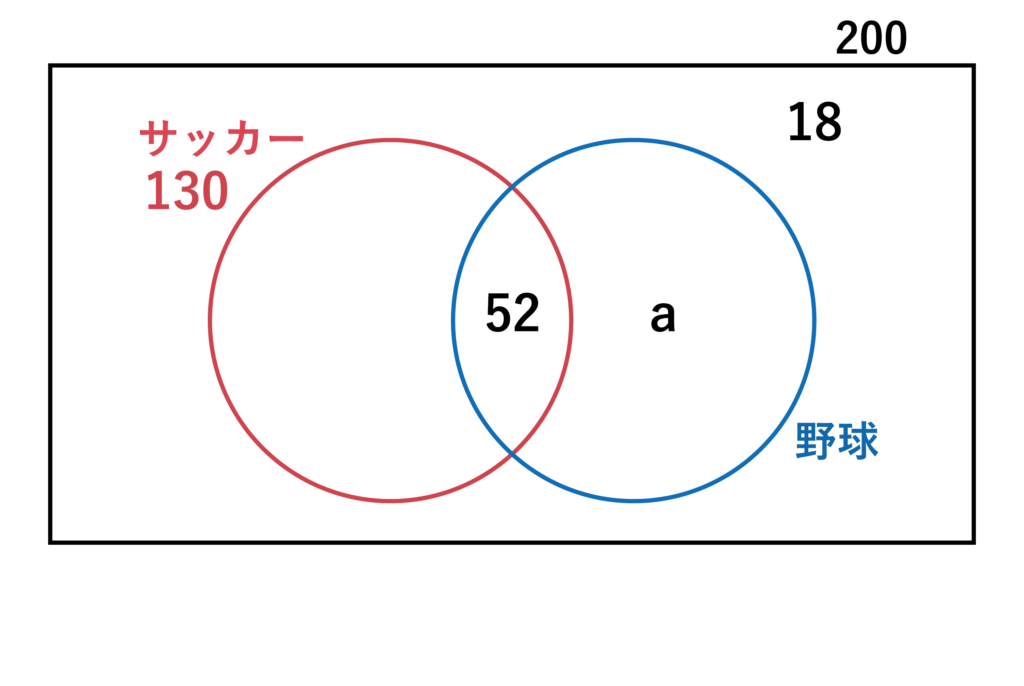
すると、130+a+18=200という方程式が立てられるので、a+148=200より、a=52であることがわかります。
よって、野球が好きな人(青い円の部分)は52+52=104[人]・・・(答)であることがわかります。
【練習問題3】
社会人50人に購読している新聞についてアンケートをとったところ、P新聞を購読している人は28人、Q新聞を購読している人は20人、R新聞を購読している人は14人であることがわかった。
また、どれも購読していないという人はおらず、P新聞もQ新聞も購読している人は8人だった。このとき、R新聞だけ購読している人の人数を求めよ。
【解答&解説】
問題文の情報をベン図にすると以下のようになり、a+b=8であることがわかります。
そして、今回求めるR新聞だけ購読している人=cに該当します。
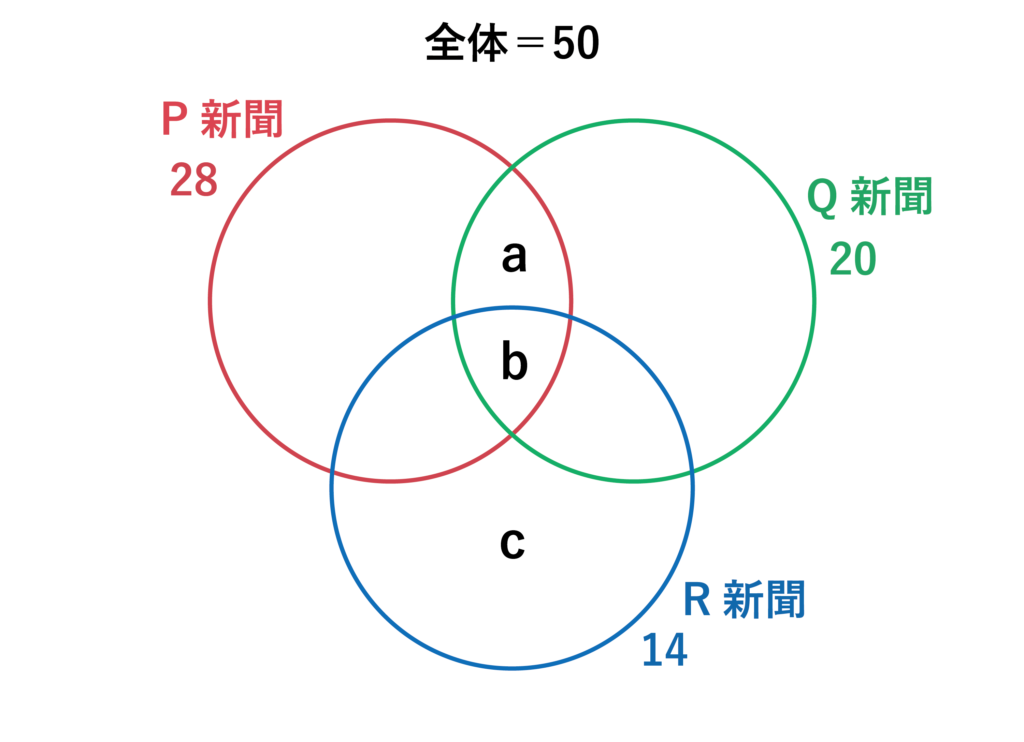
どれも購読していないという人はいないので、R新聞だけ購読している人=全体の50人からPかQ購読している人を引けば良いですね。
よって答えは50-(28+20-8)=10[人]・・・(答)であることがわかります。
🔽 本にも載ってない極秘情報 🔽
いかがでしたか?
今回はSPIの集合・ベン図問題を取り上げました。難易度が少し高い問題が多いですが、SPIの対策に余裕がある人はぜひ勉強しておきましょう。


