
SPIの非言語(数学・計数)ではグラフの領域に関する問題が出題される可能性がありますが、ペーパーテストでしか出題されないので勉強・対策の優先度は低いです(後ほど詳しく解説します)
※「SPIとは?対策方法や問題・例題をすべて紹介!適性検査SPIはこれで完璧だ!」もぜひ合わせてご覧ください。
しかし、ペーパーテスト型のSPIを受検する人も稀ではありますがいると思うので、本サイトでも念のためグラフの領域を取り上げます。
本記事ではSPIについて日本で最も熟知しているSPIマスターの私カズマがSPIのグラフの領域の問題を解くために必ず覚えるべき知識をご紹介した後、解き方についても例題でわかりやすく解説していきます。
数学が苦手な就活生や転職活動中の社会人はぜひ最後までご覧ください。
※「SPIの非言語(数学)を完全解説!対策方法やできない人でも点数を上げる方法!問題もご紹介」もぜひ合わせてご覧ください。
ちなみにですが、SPIにはたった3時間の勉強でSPIが通過してしまう勉強法があります。
これさえあれば限りなく少ない努力で内定に大きく近づきます。
これは私が100回以上ものSPI受検を通して生み出した、どの本にも載っていない超コスパの良い究極の勉強法です。
興味のある人はぜひ以下のボタンからその方法をチェックしてみてください。
目次
【SPI】グラフの領域の基礎知識
まずはSPIで出題されるグラフの領域の問題を解くために必要な基礎知識から解説していきます。
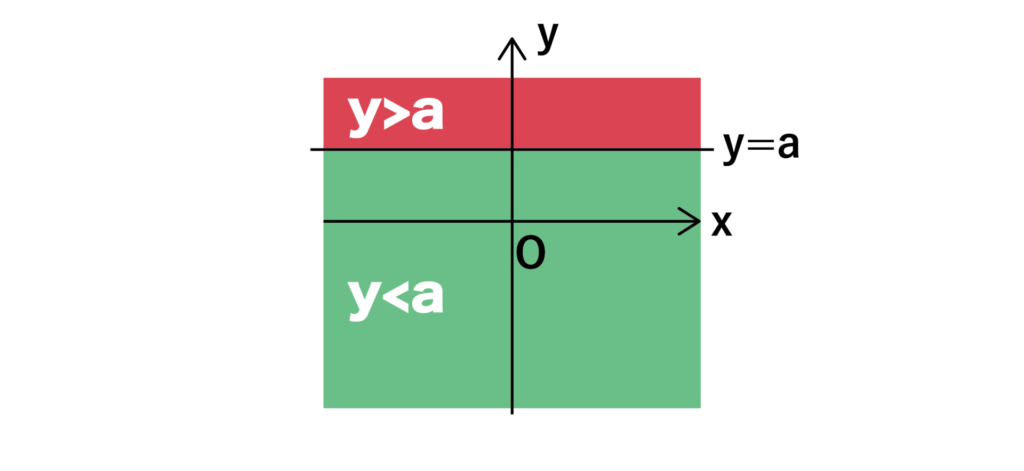
xy平面において、y=aがあるとします。このとき、y>aは以下の図における赤色の領域となり、y<aは緑色の領域となります。
※Oは原点(0, 0)を表しています。
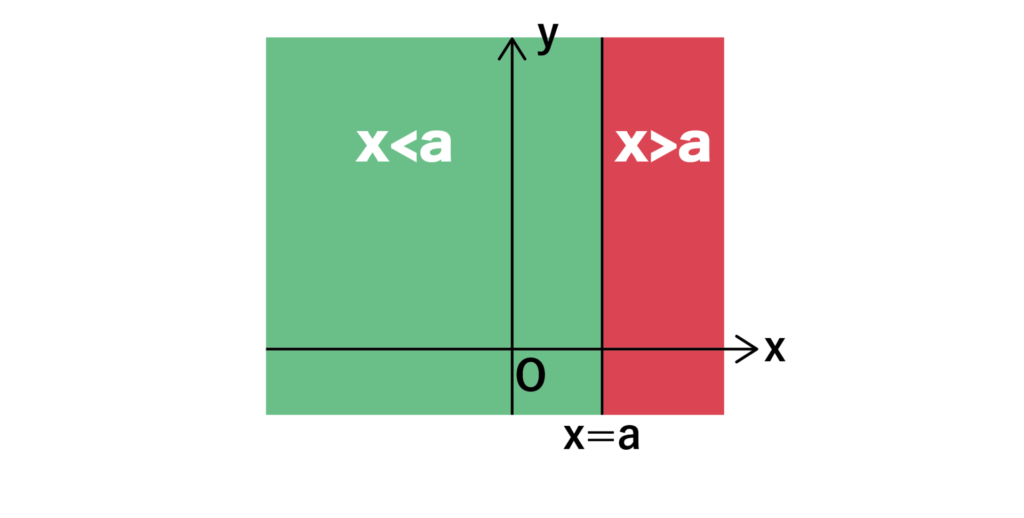
また、x=aがあるとき、x>aは以下の図における赤色の領域となり、x<aは緑色の領域となります。
以上は非常に基礎的な知識なので、必ず覚えておきましょう。
【SPI】グラフの領域で覚えておくべきグラフの形
SPIのグラフの領域の問題を解くためには、以下でご紹介する関数のグラフの形を理解しておくと便利です。
全て中学・高校の数学で学習した内容なので、忘れてしまった人は思い出していってください。
1:y=〇〇のグラフ
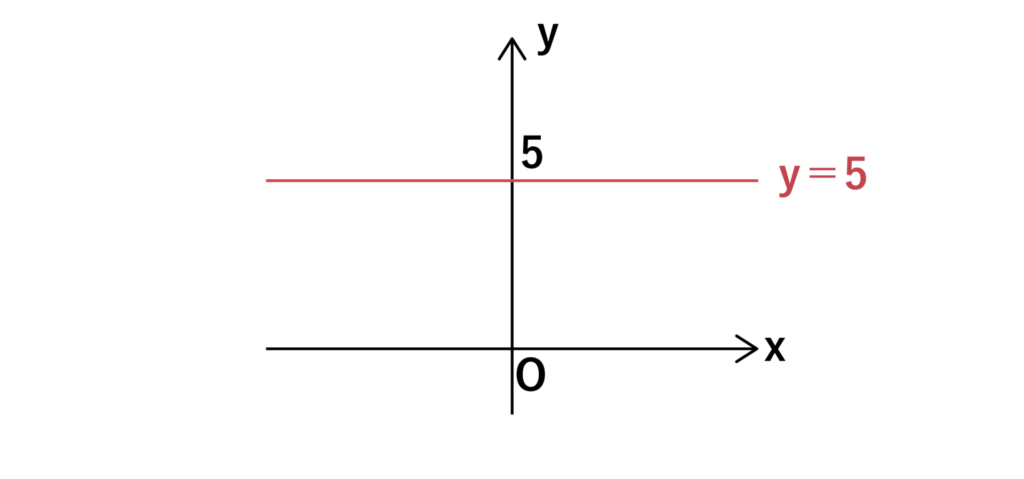
まず1つ目はy=〇〇のグラフです。以下の図はy=5のグラフです。
y=5ではxがどんな値をとってもyの値は常に5になります。なので、以下のようにx軸と並行なグラフになります。
2:x=〇〇のグラフ
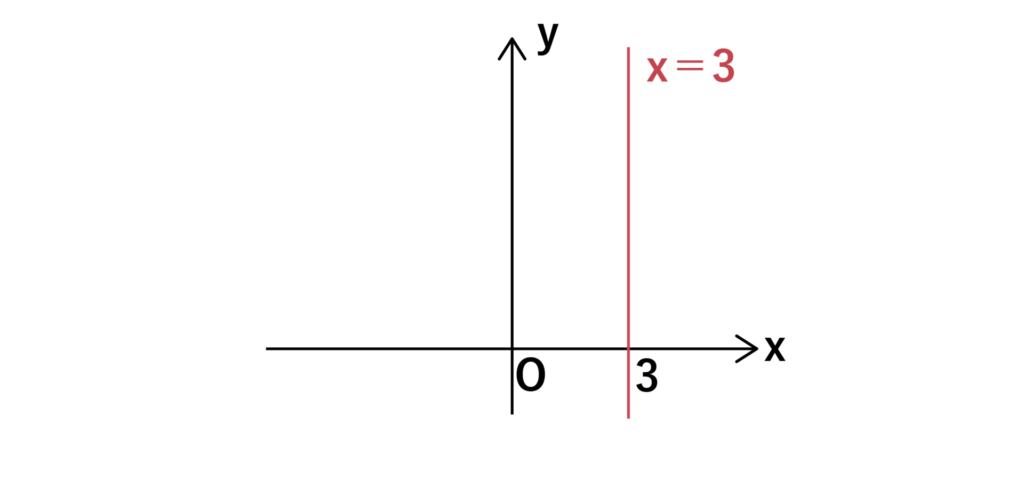
続いてはx=〇〇のグラフです。以下の図はy=3のグラフとなります。
y=3ではyがどんな値をとってもxの値は常に3になります。なので、以下のようにy軸と並行なグラフになります。
3:一次関数のグラフ
続いては一次関数のグラフです。一次関数のグラフは必ず直線のグラフになります。
以下の図はy=x+3のグラフです。
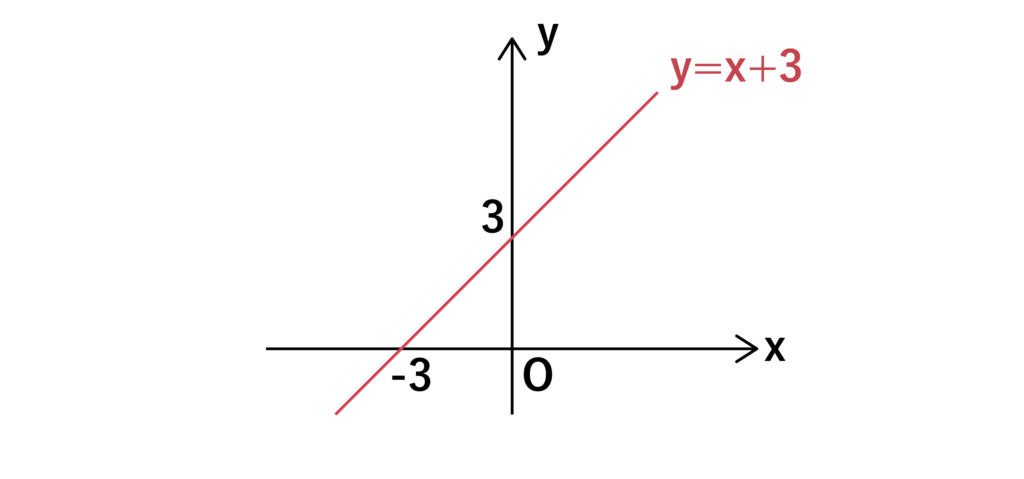
一次関数のグラフの式はy=ax+bで表すことができ、a>0のときは直線は右肩上がり、a<0のときは直線は右肩下がりになります。
以上の図において、y>x+3が示す領域はy=x+3よりも上の部分になります。
y<x+3が示す領域はy=x+3よりも下の部分になります。
4:二次関数のグラフ
続いては二次関数のグラフです。二次関数のグラフは必ず放物線状のグラフになります。
以下はy=x2+2のグラフです。
y>x2+2が示す領域はy=x2+2よりも上の部分になり、y<x2+2が示す領域はy=x2+2よりも下の部分になります。

そして、以下はy=-x2+2のグラフです。y>-x2+2が示す領域はy=-x2+2よりも上の部分になり、y<-x2+2が示す領域はy=-x2+2よりも下の部分になります。

二次関数のグラフはx2の係数が正の数のときは下に凸な放物線状に、負の数のときは上に凸な放物線状になります。
5:円のグラフ
最後は円のグラフです。以下の図のように半径が2の円はx2+y2=22となります。
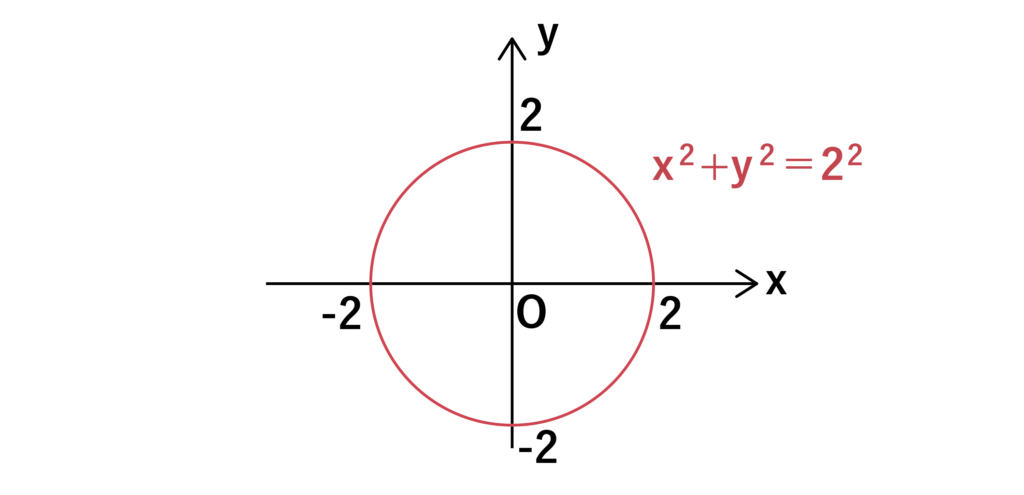
以上の図においてx2+y2>22が示す領域は円の外側、x2+y2<22が示す領域は円の内側となります。
🔽 本にも載ってない極秘情報 🔽
【SPI】グラフの領域の例題と解き方
以上でご紹介した知識を頭に入れた上で、SPIで出題されるグラフの領域の問題を1つ解いてみましょう。
※SPIの練習問題433問をすべて無料で掲載している記事もぜひ参考にしてください。
【例題】
以下の図のように、xy平面上にy=x+2とy=x2のグラフが描かれている。
このとき、
- y>x2
- y<x+2
からなる連立不等式で表される領域はA〜Jのどこかすべて答えよ。
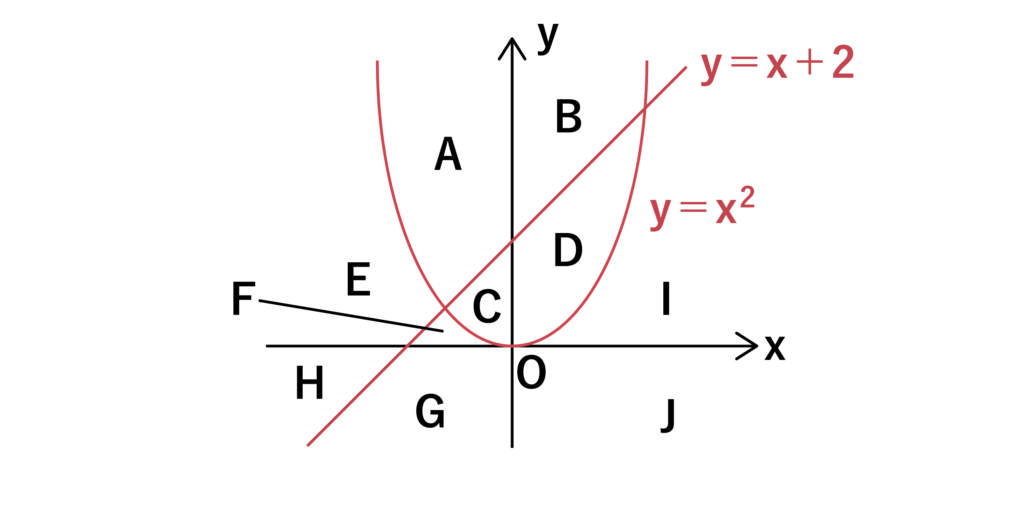
【解答&解説】
まず、y>x2が表すグラフの領域はy=x2よりも上の部分なのでA・B・C・Dの4つですね。
そして、y<x+2が表すグラフの領域はy=x+2よりも下の部分なのでC・D・F・G・I・Jの6つです。
共通している領域はCとDなので、答えはCとD・・・(答)になります。
【SPI】グラフの領域はペーパーテストでしか出題されない
冒頭でも解説しましたが、SPIにおいてグラフの領域はペーパーテストでしか出題されません。
SPIにはテストセンター、WEBテスティング、インハウスCBT、ペーパーテストという4つの受検方式がありますが、90%以上の企業はテストセンターかWEBテスティングを採用しているため、ペーパーテスト型のSPIを受検する人はほとんどいないでしょう。
※SPIのテストセンターとは何かについて詳しく解説した記事もぜひ参考にしてください。
なので、SPIを受検予定の人はグラフの領域の勉強・対策の優先度は低くして問題ありません。
SPIの勉強・対策の優先度が高いのは出題頻度が高くて難易度がそこまで高くない(=対策しやすい)分野です。例としては割合と比や速度算などがあげられます。
※「【SPI】割合と比の練習問題20問!難しい?公式や解き方・コツもわかりやすく解説!」もぜひ参考にしてください。
【SPI】グラフの領域の練習問題
最後にグラフの領域の練習問題をご用意しました。SPIのペーパーテストで出題される問題の難易度に近い練習問題となっていますので、ペーパーテストを受検予定の就活生や転職活動中の社会人はぜひ解いてみてください。
※「【SPI】転職・中途採用の対策法や問題・通過率などをSPIマスターが完全解説」もぜひ参考にしてください。
【練習問題】
以下の図のようにx2+y2=92とy=-x-2のグラフがxy平面上に描かれている。このとき、領域Aの部分を表現するためには
- x2+y2=92
- y=-x-2
- x=0
の「=」の部分をどちらの不等号(「<」または「>」)に変換すればよいかそれぞれ答えよ。
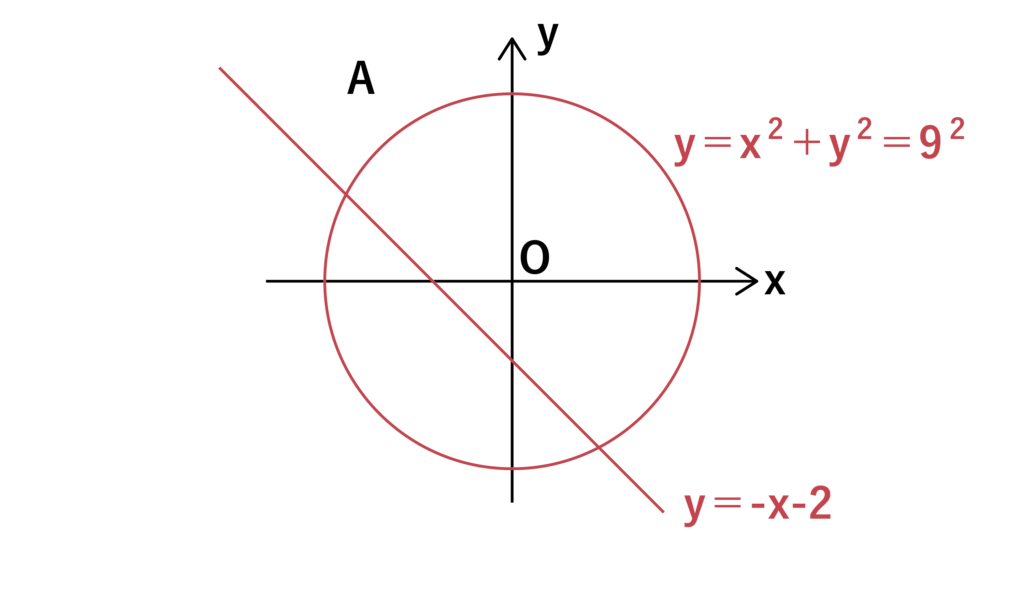
【解答&解説】
領域Aはx2+y2=92の外側に存在しているので、x2+y2>92・・・(答)であることがわかります。
また、y=-x-2の上側に存在しているのでy>-x-2・・・(答)であることがわかります。
さらに、x=0の左側に存在しているのでx<0・・・(答)であることがわかります。
🔽 本にも載ってない極秘情報 🔽
いかがでしたか?
今回はSPIのグラフの領域を解くために覚えておくべき知識や例題をご紹介していきました。
繰り返しにはなりますが、ペーパーテスト型のSPIを受検するのはかなりのレアケースです。
SPIを受検予定の人はグラフの領域の勉強・対策を重点的にやる必要はないので十分ご注意ください。
※「SPIの対策方法・勉強法を日本一SPIに詳しい筆者が真剣に考えてみた」もぜひ合わせてご覧ください。


