
SPIの非言語(数学)で展開図の問題は出るのか気になっている人もいるのはないでしょうか。
※SPIの非言語(数学)を完全解説した記事もぜひ合わせてご覧ください。
結論から述べると、SPIで展開図の問題は出ないので対策は不要です(後ほど詳しく解説します)
※「SPIの対策方法・勉強法を日本一SPIに詳しい筆者が真剣に考えてみた」もぜひ合わせてご覧ください。
本記事ではSPIと展開図の問題について図解でわかりやすく解説していきます。
SPIを受検予定の就活生や転職活動中の社会人はぜひ最後までご覧ください。
ちなみにですが、SPIにはたった3時間の勉強でSPIが通過してしまう勉強法があります。
これさえあれば限りなく少ない努力で内定に大きく近づきます。
これは私が100回以上ものSPI受検を通して生み出した、どの本にも載っていない超コスパの良い究極の勉強法です。
興味のある人はぜひ以下のボタンからその方法をチェックしてみてください。
【SPI】展開図とは?図解でわかりやすく解説
まずは展開図とは何かについて解説しておきます。
展開図とは立体を辺にそって切り開き、各面を平面上に広げた図形のことです。
例えば、サイコロの展開図は以下のようになります。
※サイコロは向かい合う面の数の和が必ず7になります。
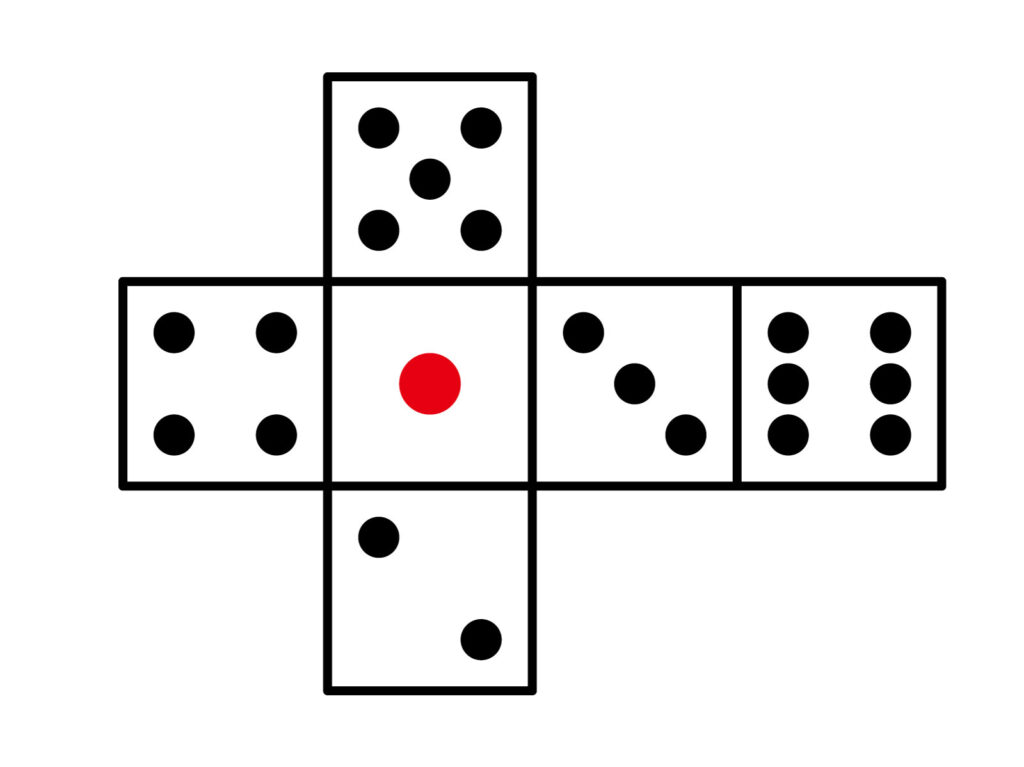
展開図の問題は組み立ててできる立体の辺や面の位置関係などをイメージしながら解いていく必要があります。
重なる辺や頂点に注意し、隣り合う面や頂点などを確認していきましょう。
展開図の問題例は以下の通りです。
【例題】
以下A〜Eの展開図のうち、立方体にならないものはどれか答えよ。
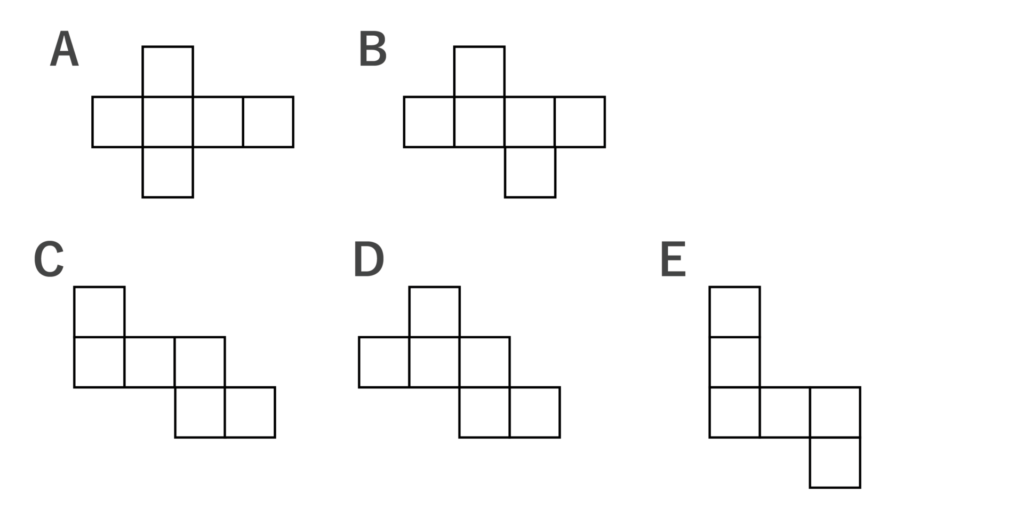
【解答&解説】
立方体の展開図は以下の11種類あります。

以上11種類のうち、Eと同じ展開図はないので、答えはEとなります。
SPIで展開図の問題は出る?
本記事の冒頭でも述べた通り、SPIで展開図の問題は出ません。
なので、SPIを受検予定の就活生や転職活動中の社会人は展開図の勉強・対策はしないようにしましょう。
現在、企業が導入しているSPIはSPI3と言われています。3はバージョン3を意味しています。
SPIは1963年にその原型が開発されました。その後は改良が重ねられ、2002年にはSPI2が、2013年にSPI3がリリースされました。
※詳しくは「SPI3とは?問題例や問題集・対策法は?SPI3-Gとは?すべてがわかる!」をご覧ください。
展開図の問題は初期のSPIやSPI2では出題されていたようですが、SPI3からは出題されなくなりました。
初期のSPIやSPI2は今は販売されていません。現在、企業が導入しているSPIはすべてSPI3となります。
本記事の筆者は今までにSPI3を100回以上も受検してきましたが、展開図の問題が出題されたことは一度もありませんのでご安心ください。
ちなみにですが、公務員試験の数的処理という科目では展開図の問題が出題されるのでご注意ください。
公務員試験の数的処理はSPIの非言語と似た科目ですが、難易度は圧倒的に数的処理の方が難しいです。
詳しくは「SPIと数的処理の問題を徹底比較!できない人が多いのはどっち?」で解説しているので、公務員への就職・転職を視野に入れている人はぜひ参考にしてください。
【SPI】展開図の練習問題
最後に、展開図の練習問題を2問ご用意しました。
SPIでは出題されませんが、公務員試験の受検を検討している人や展開図の問題に興味のある人はぜひ解いてみてください。
【練習問題1】
以下のような立方体がある。
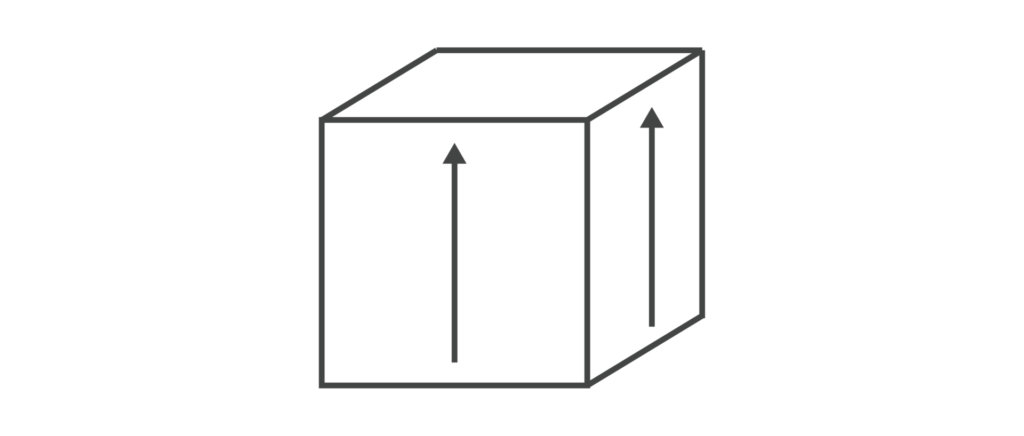
この立方体の展開図として正しいものは以下A〜Cのうちどれか答えなさい。
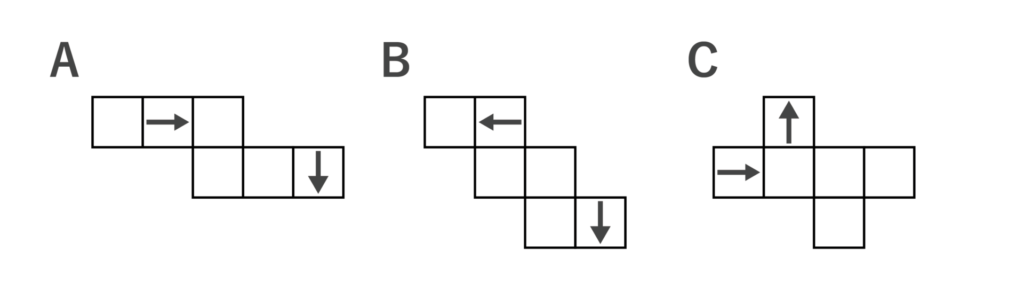
【解答&解説】
答えはBです。AとCは隣り合う矢印の向きが逆になります。
【練習問題2】
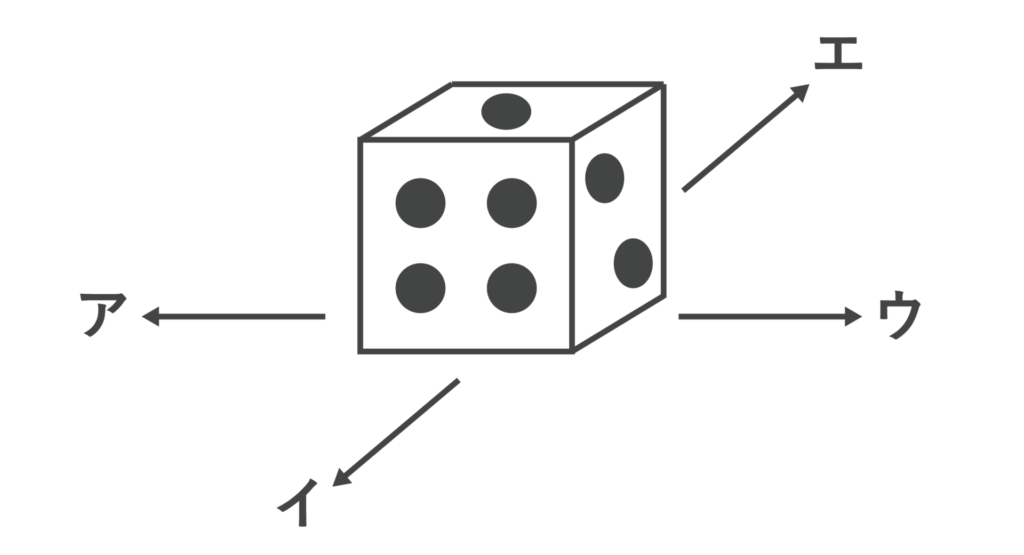
以下のようなサイコロを転がす。ウ 9回→エ 13回→イ 12回→ア 7回という順に転がしたとき、サイコロの上の面に出る目はいくつになるか答えなさい。
【解答&解説】
答えは6です。
サイコロは同じ向きに続けて4回転がすと元の面に戻るので、回転数が4回以上のときは4で割ったあまりを考えます。
- ウ 9回:9÷4=2あまり1
- エ 13回:13÷4=3あまり1
- イ 12回:12÷4=3あまり0
- ア 7回:7÷4=1あまり3
より、イの12回はあまりが0なので考えず、アの7回はあまりが3なので、ア 3回と考えてもよいのですが、逆方向のウに4-3=1[回]と考えて以下のような図で表すことも可能です。

展開図の練習問題は以上となります。
🔽 本にも載ってない極秘情報 🔽
今回はSPIと展開図の関係について解説していきました。展開図は脳内で考えると混乱しがちです。
必ずメモを取るなどして、視覚的にわかるようにした状態で問題を解き進めましょう。


