
SPIの非言語(数学・計数)では図形の面積を求める問題が出題されるのか気になっている就活生や転職活動中の社会人も多いのではないでしょうか。
今回はSPIに関して日本トップレベルに熟知している私カズマが、今までにSPIを100回以上も受検してきた体験をもとにSPIで図形の面積を求める問題は出題されるのか?について解説していきます。
本記事では図形の面積を求めるための公式や方法もご紹介しているので、ぜひ最後までご覧ください。
※「SPIの非言語(数学)を完全解説!対策方法やできない人でも点数を上げる方法!問題もご紹介」もぜひ合わせてご覧ください。
ちなみにですが、SPIにはたった3時間の勉強でSPIが通過してしまう勉強法があります。
これさえあれば限りなく少ない努力で内定に大きく近づきます。
これは私が100回以上ものSPI受検を通して生み出した、どの本にも載っていない超コスパの良い究極の勉強法です。
興味のある人はぜひ以下のボタンからその方法をチェックしてみてください。
目次
SPIで図形の面積を求める問題は出ない
早速結論を述べてしまいましたが、SPIでは図形の面積を求める問題は出題されません。
※SPIではWEBテスティング、テストセンター、インハウスCBT、ペーパーテストの4つの受検方式がありますが、すべての受検方式において図形の面積を求める問題は出題されません。
※SPIのテストセンターとは何かについて詳しく解説した記事もぜひ参考にしてください。
SPIに関して日本トップレベルに熟知している私は今までにSPIを100回以上も受検してきていますが、図形の面積を求める問題が出題されたことは一度もありません。
現時点では勉強・対策の優先度はかなり低いですが、今後もSPIで図形の面積を求める問題が出題されることは絶対にないと言い切ることはできませんので、以下からは図形の面積を求めるための公式や方法を念の為おさらいしておきます。
【SPI】図形の面積の公式・求め方
図形の面積の公式や求め方は中学で学習しますが、忘れてしまった人もいるかと思いますのでこれを機に復習しておきましょう。
今回は以下の公式をご紹介していきます。
- 三角形の面積
- 平行四辺形の面積
- ひし形の面積
- 台形の面積
- 円の面積
- 扇形の面積
では、順番に解説していきます。
三角形の面積の求め方(公式)
まずは三角形の面積の求め方からです。三角形の面積の公式は底辺×高さ÷2です。
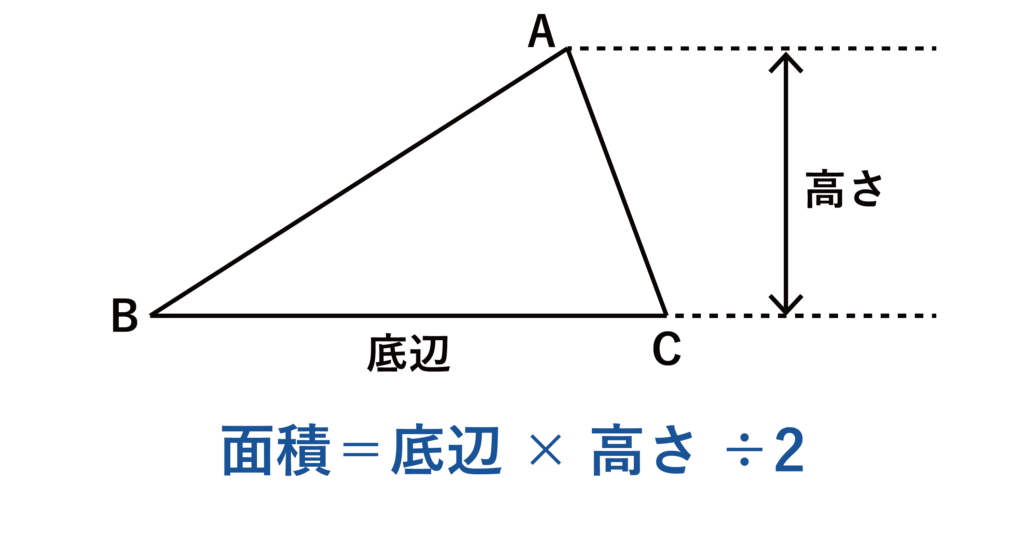
例えば、上記の図において底辺BC=8、高さ=10の三角形の面積は8×10÷2=40となります。
平行四辺形の面積の求め方(公式)
平行四辺形の面積は底辺×高さで求めることができます。三角形の面積を求めるときのように2で割る必要はないのでご注意ください。
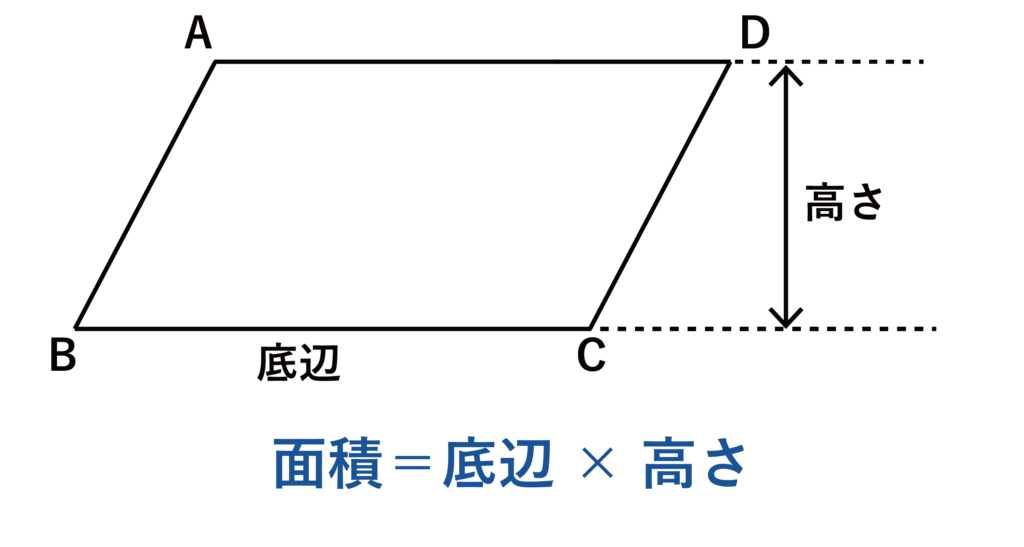
例えば、上記の図において底辺BC=20、高さ=8の平行四辺形の面積は20×8=160となります。
ひし形の面積の求め方(公式)
ひし形の面積は対角線×対角線÷2で求めることができます。
対角線は2本ありますが、長さが違う場合もあれば同じ場合もあります(2本の対角線の長さが同じ四角形を正方形と言います)
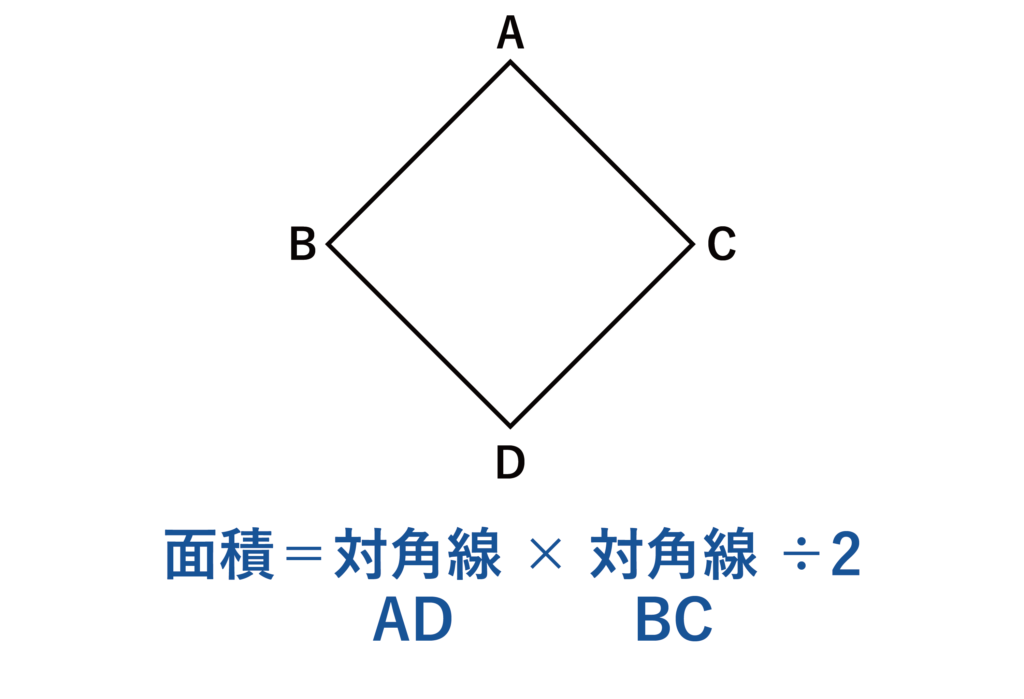
例えば、上記の図において対角線AD=12、対角線BC=10のひし形の面積は12×10÷2=60となります。
台形の面積の求め方(公式)
台形の面積は(上底+下底)×高さ÷2で求めることができます。上底とは上にある辺のことで、下底とは底辺のことです。
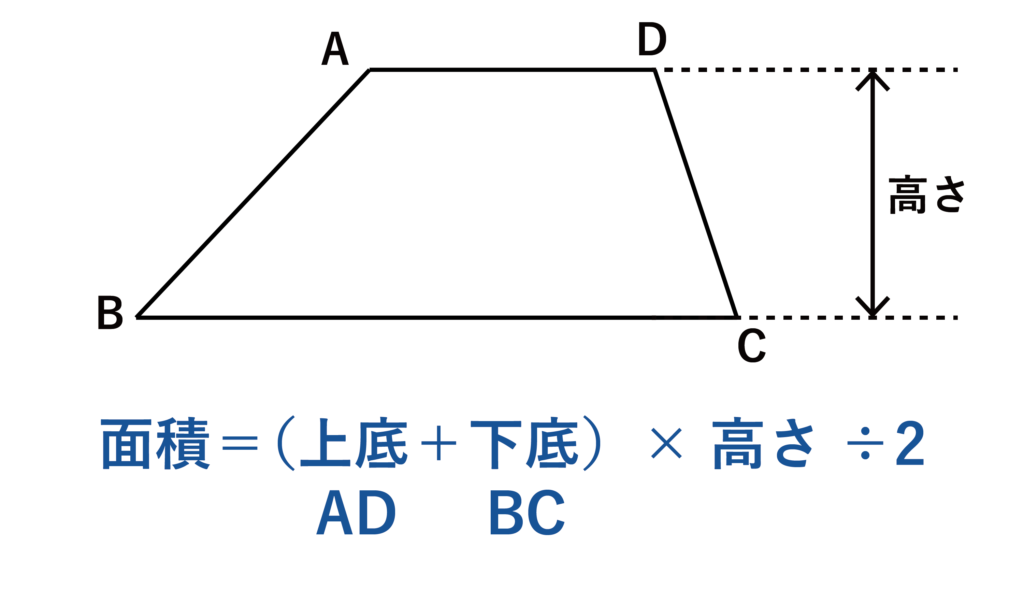
例えば、上記の図において上底AD=10、上底=26、高さ=6の台形の面積は(10+26)×6÷2=108となります。
🔽 本にも載ってない極秘情報 🔽
円の面積の求め方(公式)
円の面積は半径×半径×πで求めることができます。記号πはパイと読み、円周率を表します。
円周率は3.141592・・・と無限に続くため書き切ることができません。なので、πを使って表現するのです。
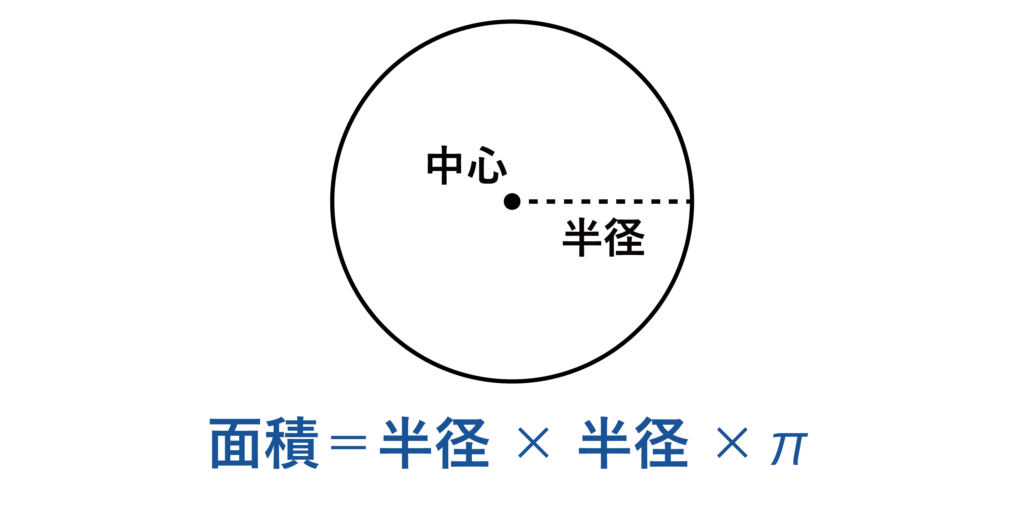
例えば、上記の図において円の半径=6の場合の円の面積は6×6×π=36πとなります。
問題によっては「円周率は3.14を使いなさい」といった指示が出る場合もあります。
そのような指示が出た場合、半径=6の円の面積は6×6×3.14=113.04となります。
扇型の面積の求め方(公式)
最後は扇型の面積の求め方です。扇型は円の一部を切り取ってできる図形です。
扇型の面積は半径×半径×π×(中心角/360)で求めることができます。
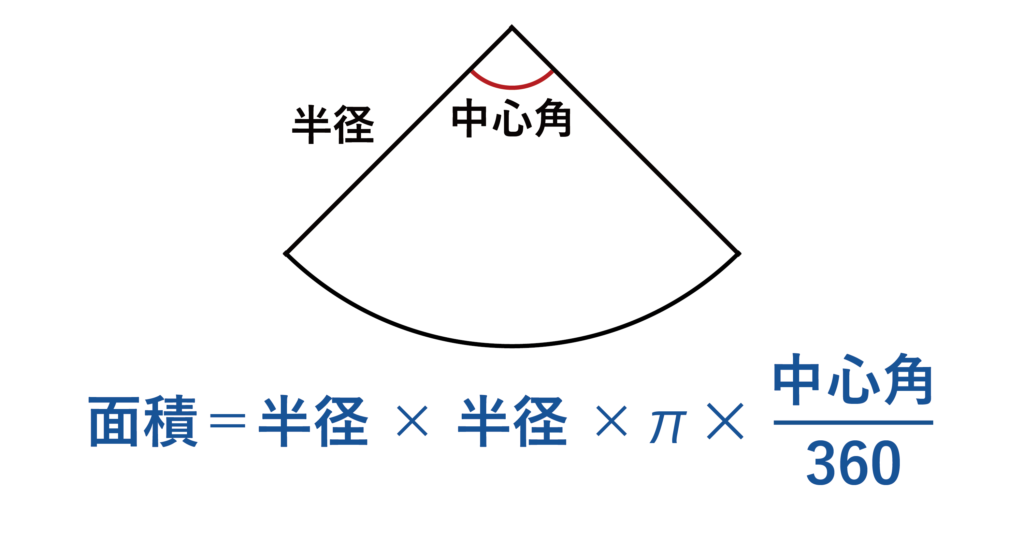
半径×半径×πで円の面積を求めることができるのでした。扇型は円の一部を切り取った図形なので、円の面積に中心角/360をかけることによって扇型の面積を求めることができます。
※360は円の1周となる360°を表しています。
例えば、半径=10、中心角=60°の扇型の面積=10×10×π×60/360=100π×1/6=50/3πとなります。
【SPI】図形の面積を求める練習問題
最後に図形の面積を求める練習問題を1問解いてみましょう。
上記でご紹介した面積の公式のどれが使えそうかを考えてみてください。
【練習問題】
以下の図における赤色の部分の面積を求めよ。ただし、四角形ABCDは正方形とし、AB=10とする。また、円周率=3.14とする。
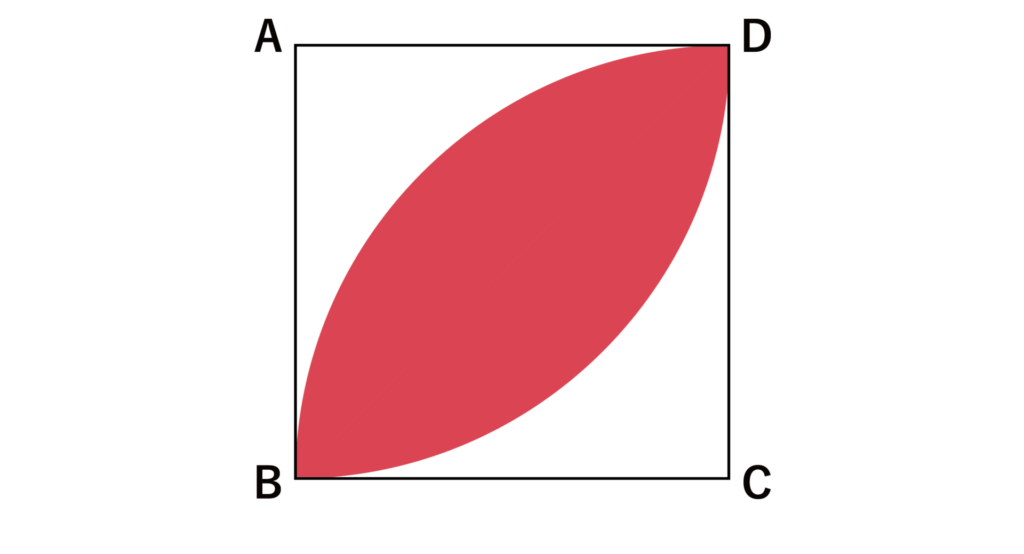
【解答&解説】
以下のように、補助線として対角線BDを引いてみましょう。
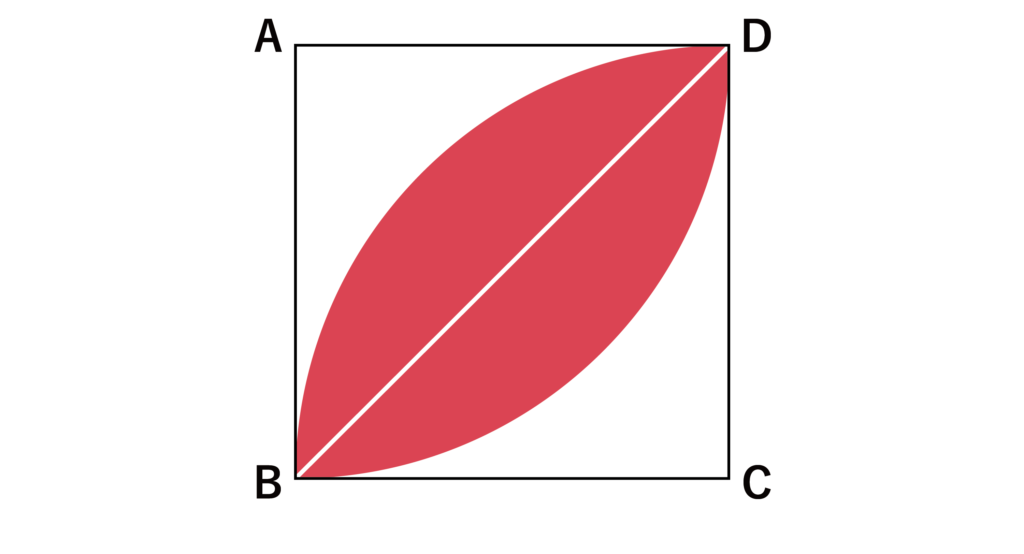
すると、以下の赤色の部分の面積は扇型BCD-三角形BCDで求めることができますね。
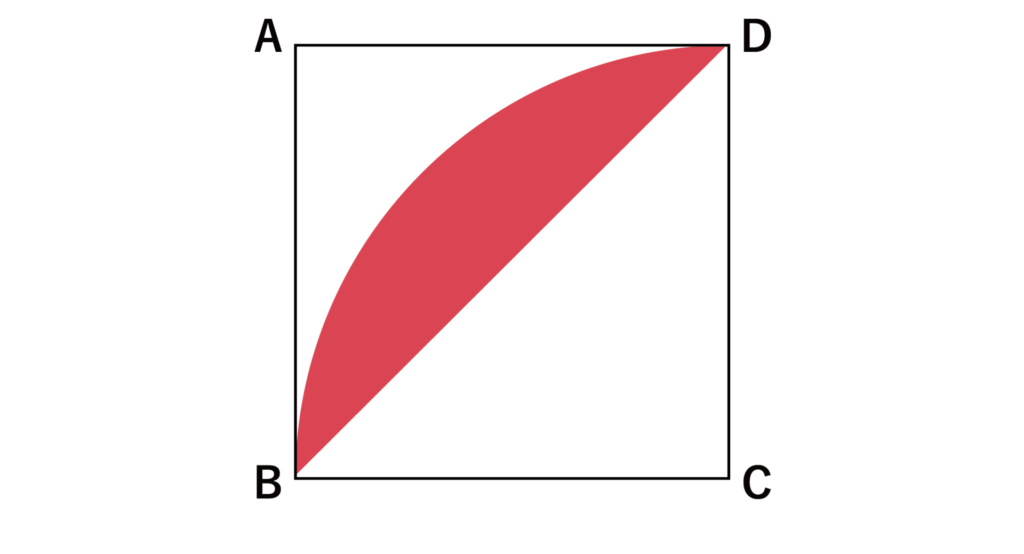
- 扇型BCDの面積=10×10×3.14×90/360=314×1/4=78.5
- 三角形BCDの面積=10×10÷2=50
より、上記の赤色の部分の面積=78.5-50=28.5となります。
求める面積は28.5の2個分なので、答えは28.5×2=57・・・(答)となります。
🔽 本にも載ってない極秘情報 🔽
いかがでしたか?
今回はSPIで図形の面積を求める問題は出題されるのか?について解説していきました。
現時点では勉強・対策の優先度は低いですが、上記でご紹介した面積の求め方・公式は一般常識に近い内容なので、余裕がある人は覚えておいた方が良いでしょう。


