
SPIの非言語(数学)では6人のメンバー問題が出題されるケースがあります。
※「SPIとは?対策方法や問題・例題をすべて紹介!適性検査SPIはこれで完璧だ!」もぜひ合わせてご覧ください。
6人のメンバー問題は場合の数に関する問題で、内容は非常にシンプルです。
解き方さえ知っていれば簡単に解ける問題なので、SPIを受検予定の就活生や転職活動中の社会人は必ず対策しておきましょう。
本記事ではSPIを日本で一番知り尽くしているSPIマスターの私カズマが、SPIで出題される6人のメンバー問題をご紹介し、解き方のポイントをわかりやすく解説していきます。
ちなみにですが、SPIにはたった3時間の勉強でSPIが通過してしまう勉強法があります。
これさえあれば限りなく少ない努力で内定に大きく近づきます。
これは私が100回以上ものSPI受検を通して生み出した、どの本にも載っていない超コスパの良い究極の勉強法です。
興味のある人はぜひ以下のボタンからその方法をチェックしてみてください。
【SPI】6人のメンバー問題とは?解き方をわかりやすく解説
SPIの非言語で出題される可能性のある6人のメンバー問題は以下のような問題です。
※SPIの非言語(数学)を完全解説した記事もぜひ参考にしてください。
制限時間は1分とします。
【例題】
6人のメンバーが2人組を2つ作って、テニスのダブルスの試合をするとき、対戦の組み合わせは全部で何通りあるか求めよ。
【解答&解説】
答えは6C2 × 4C2 ÷ 2=45[通り]・・・(答)となります。
6人のメンバーをA、B、C、D、E、Fとしてみます。
6C2で選んだ2人のメンバーが(A、B)、4C2で選んだ2人のメンバーが(C、D)だったとします。
また、6C2で選んだ2人のメンバーが(C、D)、4C2で選んだ2人のメンバーが(A、B)だったとします。
上記の2パターンは(A、B)VS(C、D)という同じ対戦カードになります。
つまり、6C2 × 4C2=90[通り]は、2通りずつのダブりが発生している状態です。
よって、最後は90を2で割る必要があります。
※「SPIで場合の数は頻出!解き方のコツと出題パターンを完全網羅!練習問題付き」もぜひ参考にしてください。

【SPI】6人のメンバー問題のポイント
以上でご紹介した6人のメンバー問題では6C2 × 4C2=90[通り]という回答をしてしまう人が多いです。
6C2 × 4C2だと2通りずつのダブりが発生しているということに気づけるかがこの問題の最大のポイントです。
ちなみに、SPIでは円順列に関する問題が出題されることもあります。
円順列とはいくつかのものや人を円形に並べる配列のことで、以下のような問題です。
【例題】
4人が手を繋いで円になるとき、並び方は全部で何通りあるか。
【解答&解説】
順列では4P4=24[通り]です。しかし、円形なので、4人をA・B・C・Dとすると、以下の4つの並びはすべて同じものとみなすことができます。
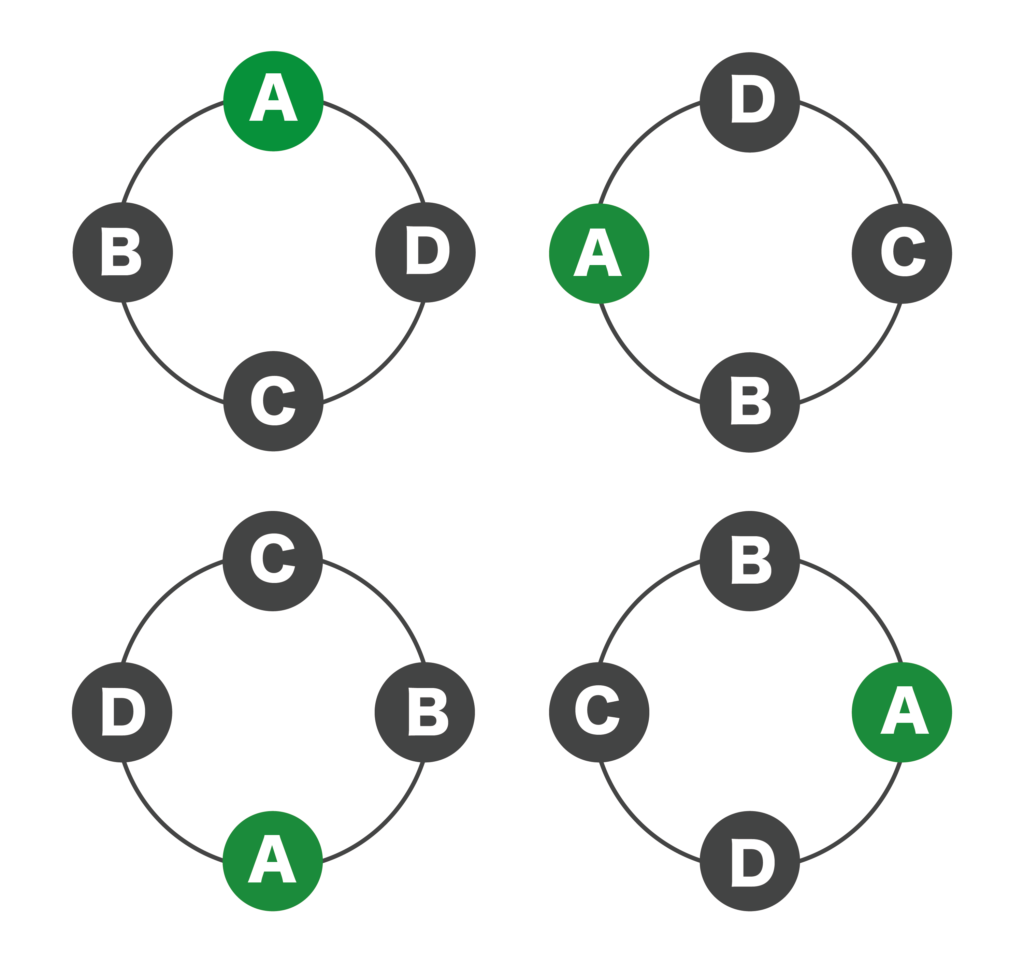
同じものを4回重複してカウントしているので、答えは24÷4=6[通り]・・・(答)となります。
円順列でも上記の通りダブりが発生しており、最後に割り算をする必要があります。
SPIを受検予定の就活生や転職活動中の社会人は必ず理解しておきましょう。
練習問題
最後に、SPIの非言語で出題される場合の数に関する練習問題をご用しました。
組み合わせと順列の公式どちらを使うか考えながら解いてみましょう。
※SPIの練習問題433問をすべて無料で掲載している記事もぜひ参考にしてください。
【練習問題1】
Aが所属する卓球チームのメンバーは全部で12人である。この12人をレビュラー9人と補欠3人に分けたい。
(1)レギュラーの組み合わせは何通りあるか。
(2)Aがレギュラーに入るとき、レギュラーの組み合わせは何通りあるか。
【解答&解説】
(1)補欠3人を選べば、レギュラー9人も決まります。
よって、12C3=(12×11×10)/(3×2×1)=220[通り]・・・(答)です。
(2)Aはレギュラーに決まっているので、A以外の11人から3人の補欠を選べばよいです。
よって、11C3=(11×10×9)/(3×2×1)=165[通り]・・・(答)となります。
【練習問題2】
P、Q、R、S、T、U、V、Wの8人を5人部屋と3人部屋に振り分ける。
(1)分け方は何通りあるか。
(2)Qが3人部屋になる分け方は何通りあるか。
【解答&解説】
(1)3人部屋に入る3人を決めれば、残り5人は5人部屋に決まります。
8人から3人を選ぶので、8C3=(8×7×6)/(3×2×1)=56[通り]・・・(答)です。
(2)3人部屋の1人はQなので、残り7人のうち2人がQと同じ3人部屋になれば、残り5人は5人部屋に決まります。
よって、7C2=(7×6)/(2×1)=21[通り]・・・(答)となります。
【練習問題3】
大人2人、子供4人の合計6人から4人を選んでリレーのチームを作る。
(1)走る順番は何通りあるか。
(2)大人2人、子供2人の合計4人を選ぶとき、走る順番は何通りあるか。
【解答&解説】
(1)順番が関係するので、6人から4人を選んで並べる順列を求めます。
6P4=6×5×4×3=360[通り]・・・(答)です。
(2)大人と子供を分けて考えます。大人2人から2人を選ぶ組み合わせの数は1通りです。
子供4人から2人を選ぶ組み合わせの数は4C2=(4×3)/(2×1)=6[通り]です。
選んだ4人の並べ方は4!=4×3×2×1=24[通り]です。
これらを掛け合わせたものが答えになるので、1×6×24=144[通り]・・・(答)となります。
🔽 本にも載ってない極秘情報 🔽
今回はSPIにおける6人のメンバー問題を取り上げました。
非常にシンプルな問題なので、解き方をしっかりマスターしてから本番のSPIに臨みましょう。


