
SPIの非言語(数学)では速度算が頻出なので必ず対策をしておきましょう。
※「SPIの非言語(数学)を完全解説!対策方法やできない人でも点数を上げる方法!問題もご紹介」もぜひ合わせてご覧ください。
本記事ではSPIの非言語(数学)で出題される速度算の問題の難易度に近い練習問題を18問ご用意しました。
コツや解き方・公式・計算方法も合わせてご紹介していきます。
SPIを受検予定の就活生や転職活動中の社会人はぜひ解いてみてください。
ちなみにですが、SPIにはたった3時間の勉強でSPIが通過してしまう勉強法があります。
これさえあれば限りなく少ない努力で内定に大きく近づきます。
これは私が100回以上ものSPI受検を通して生み出した、どの本にも載っていない超コスパの良い究極の勉強法です。
興味のある人はぜひ以下のボタンからその方法をチェックしてみてください。
目次
SPIの速度算とは?重要公式3つ
速度算とはその名の通り速度(速さ)に関する問題です。速度だけではなく距離や時間を求める場合もあります。SPIでは頻出の分野なので、SPIを受検予定の就活生や転職活動中の社会人は必ず対策しましょう。
※「【SPI】転職・中途採用の対策法や問題・通過率などをSPIマスターが完全解説」もぜひ参考にしてください。
具体的には、
- どれくらいの速度で目的地に向かえば時間通りに到着することができるのか?
- 目的地までの距離はどのくらいか?
などを計算します。
SPIの速度算を解くためには以下3つの公式を必ず覚えておかなくてはなりません。
1:距離の換算
1つ目は距離(cm・m・km)の換算です。
換算とはcmをmに変換したり、kmをmに変換したりすることです。
1km=1000mです。つまり、mをkmに変換するには1000で割れば良いことがわかります。
また、1m=100cmです。つまり、cmをmに変換するには100で割れば良いことがわかります。
kmをcmに変換するには100000で割る必要があります。
以上をまとめたのが以下の図となります。
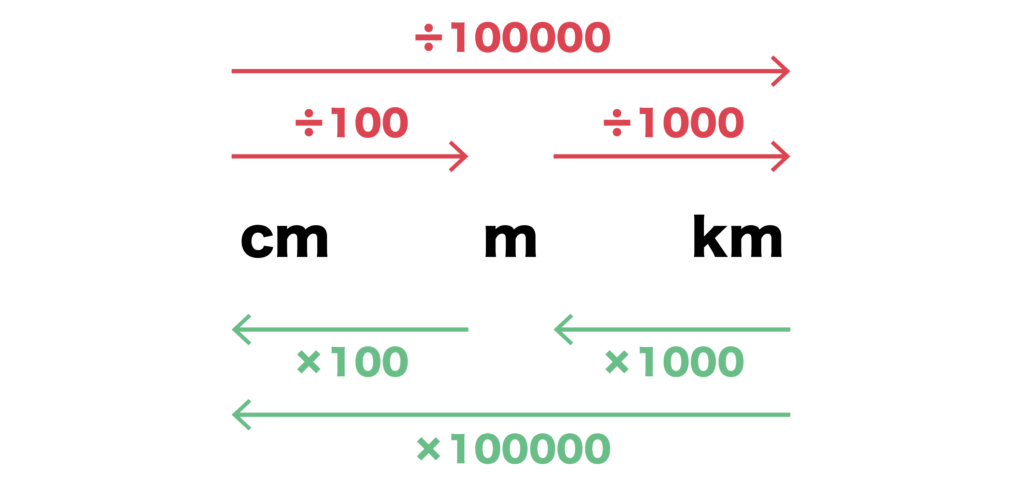
kmとcmの変換はSPIではほとんど登場しないので、無理に覚える必要はありません。
SPIではmとkmが混じった問題が登場する場合がありますので、単位の変換は必ずできるようにしておきましょう。
2:速度の換算
2つ目は速度の換算です。
例えば、速度=30m/分で歩く人がいたとします。つまり、1分で30m進むということです。
1分で30m進むので、1時間(=60分)では30×60=1800m進むことができます。
つまり、30m/分=1800m/時となります。m/分をm/時に変換するには60をかけます。
また、1分(=60秒)で30m進む場合、1秒では30÷60=0.5m進むことができます。
つまり、30m/分=0.5m/秒となります。m/分をm/秒に変換するには60で割ります。
以上をまとめた図は以下となります。
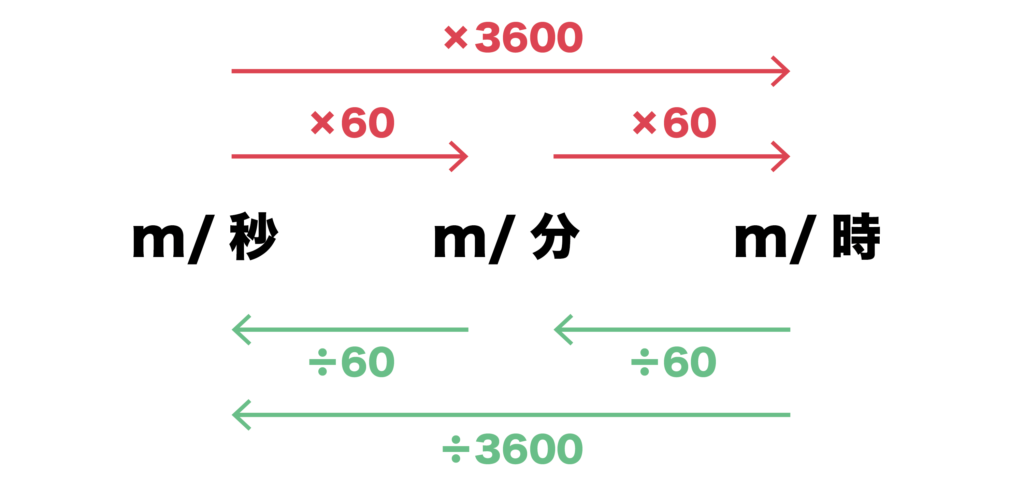
m/秒をm/時に一気に変換したいときは3600をかければ良いです。
ちなみにですが、km/秒をm/分に変換する場合など、距離の単位が違うときは必ずどちらかの距離の単位に揃えてから60をかけたり割ったりする必要がありますのでご注意ください。
例えば30km/時をm/分に変換するには、まずは30kmをmに変換します。
つまり、30km/時=30000m/時です。この後に60で割ってm/分を求めます。
したがって、30km/時=30000m/時=500m/分となります。
3:き・は・じの法則
最後は「き・は・じの法則」です。
き=距離、は=速さ(速度)、じ=時間を表しており、以下のような図にすることが可能です。

横同士(「は」と「じ」)は掛け算を表しており、上の文字は分子、下の文字は分母になります。
つまり、
- 距離=速さ×時間
- 速さ=距離÷時間
- 時間=距離÷速さ
で求めることができます。
これはSPIの速度算では必ず使用するので絶対に覚えておきましょう。
🔽 本にも載ってない極秘情報 🔽
【SPI】速度算の例題と計算方法・解き方のコツ
では、以上でご紹介した公式を頭に入れながらSPIの速度算の例題を1問解いてみましょう。
【例題】
家から目的地まで6.3km/時の速さで走ったところ、4.2km/時の速さで歩いた時に比べて3分速く着いた。この時、家から目的地までの距離は何mか求めよ。
【解答&解説】
SPIではこの例題のようにkmやm、分や時間など様々な単位が混ざって出題されることがよくあります。
SPIの速度算を解く際には、必ず単位をそろえることを意識してください。
今回は家から目的地までの距離を求めるので、それをa[m]とおいてみます。
また、6.3km/時=6300m/時=105m/分、4.2km/時=4200m/時=70m/分ですね。
すると、6.3km/時の速さで走って目的地まで行った場合、a/105[分]かかることがわかります。
同様に考えて、4.2km/時の速さで歩いて目的地まで行った場合、a/70[分]かかることがわかります。
すると、問題文よりa/105=a/70-3という方程式を立てることができますね。
両辺に210をかけると、2a=3a-630となるので、a=630[m]・・・(答)となります。
※方程式の解き方がわからない人はSPIで絶対必要な方程式について解説した記事をご覧ください。
【SPI】速度算:すれ違い・追い越しの例題と計算方法
先ほどご紹介した速度算の例題は非常に基本的な問題となります。
SPIでは基本的な問題も出題されますが、少し難易度が上がったすれ違い・追い越しに関する問題もたまに出題されるので、念のため例題で解き方を確認しておきましょう。
【例題:すれ違いの速度算】
20m/秒で走っている長さ80mの電車と16m/秒で走っている長さ100mの電車が向かい合って進んでいる。このとき、2つの電車が出会ってから離れるまでにかかる時間は何秒か求めよ。
【解答&解説】
速度算において「すれ違う」というのは電車の先頭が出会ってから電車のお尻が離れるまでのことを指します。
今回の場合だと、以下の図のように電車の先頭が出会ってから電車のお尻が離れるまでに合計で80+100=180mの距離が生まれ、速度は20m/秒+16m/秒=36m/秒でその180mを通るので、求める時間は180÷36=5[秒]・・・(答)となります。
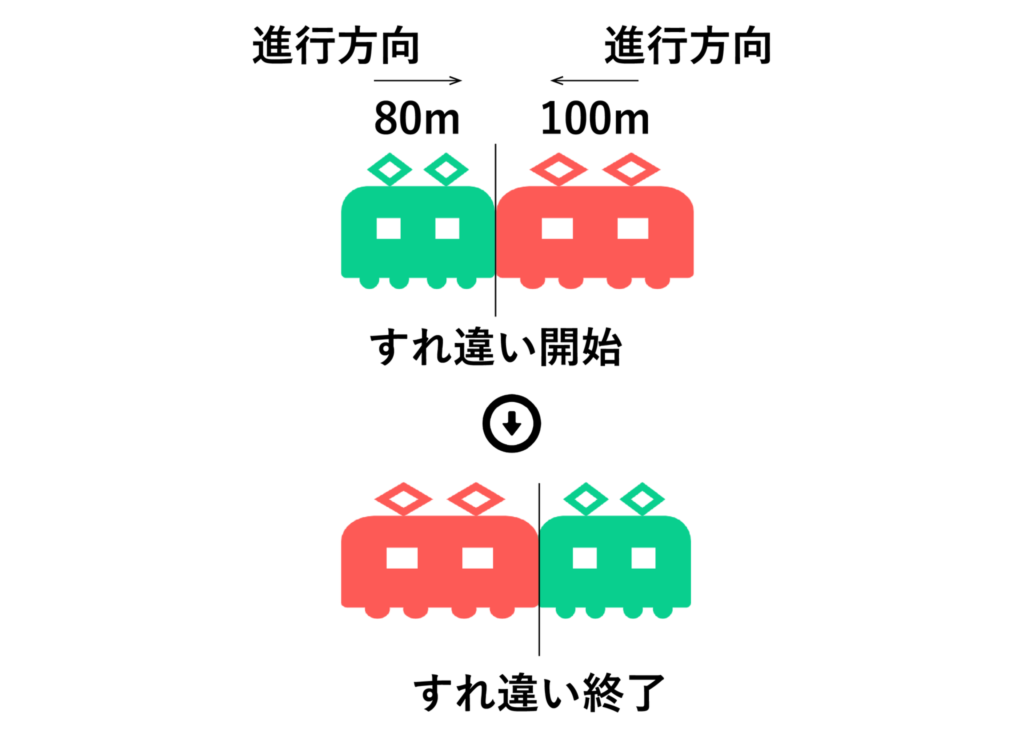
続いては、電車が電車を追い越すパターンについて解説していきます。
【例題:追い越しの速度算】
20m/秒で走っている長さ80mの電車Aと16m/秒で走っている長さ100mの電車Bが同じ方向に進んでいる。このとき、電車Aが電車Bに追いついてから追い越すまでに何秒かかるか求めよ。
【解答&解説】
速度算において「追いつく」というのは速度が速い方の電車の先頭が遅い方の電車のお尻に追いつくことを指しており、「追い越す」というのは、速度が速い方の列車のお尻が遅い方の列車の先頭を追い越すことを指します。
今回の場合だと、電車Bよりも電車Aの方が速いので以下の図のようになります。
電車Aの先頭が電車Bのお尻に追いついてから、電車Aのお尻が電車Bの先頭を追い越すまでに合計で80+100=180mの距離が生まれ、速度の差である20m/秒-16m/秒=4m/秒でその180mを通るので、求める時間は180÷4=45[秒]・・・(答)となります。
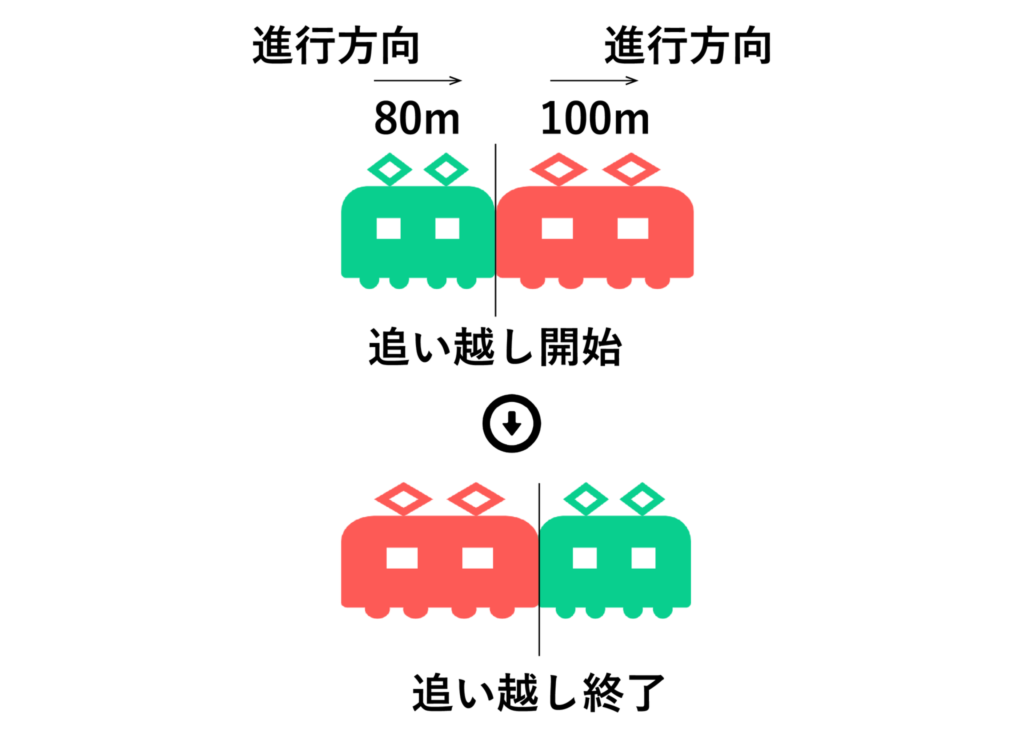
- すれ違いの時間=電車の長さの和÷電車の速度の和
- すれ違いの時間=電車の長さの和÷電車の速度の差
は非常に重要なので、公式として覚えておきましょう。
🔽 本にも載ってない極秘情報 🔽
SPIで速度算が出題される受検方式と難易度
冒頭でも解説した通り、SPIではすべての受検方式(WEBテスティング・テストセンター・インハウスCBT・ペーパーテスト)において速度算が出題範囲に含まれています。
※SPIのWEBテスティングを完全解説した記事もぜひ合わせてご覧ください。
出題頻度は高く、出題される問題も基本的なものが多いです。応用問題はほとんど出題されません。
※「SPIは難しい?難しすぎる?難易度(レベル)を言語と非言語別に解説!苦手・苦手すぎる人がやるべきことは?」もぜひ参考にしてください。
上記の通り、覚える公式は少し多いかもしれませんが、出題頻度が高いかつ基本的な問題が出題される傾向にあるので速度算の勉強・対策をすることはSPIの点数を上げるために非常に有効な手段と言えます。
ちなみにですが、速度算以外に出題頻度が高くて基本的な問題が出題される傾向にある分野は割合と比、損益算です。
※「【SPI】割合と比の練習問題20問!難しい?公式や解き方・コツもわかりやすく解説!」もぜひ参考にしてください。
【SPI】速度算の練習問題
上記でも解説した通り、SPIの速度算を解くためには以下3つの公式を必ず理解しておかなければなりません。
- 距離の換算(1km=1000m、1m=100cmなど)
- 速度の換算(60m/分=3.6km/時など)
- き・は・じの法則
以上をしっかりと理解できてから、以下の練習問題を解くようにしましょう。
※SPIの練習問題433問をすべて無料で掲載している記事もぜひ参考にしてください。
【練習問題1】
家から駅まで時速6kmで歩いたところ12分で到着した。翌日は時速4kmで歩いたとすると、何分で駅まで到着するか求めよ。
【解答&解説】
12分=12/60[時間]ですね。
よって駅までの距離は6 × 12/60=6/5[km]であることがわかります。
よって時速4kmで歩いた場合は6/5 ÷ 4=3/10[時間]かかることがわかります。
3/10時間=18[分]なので、答えは18分・・・(答)となります。
【練習問題2】
家から2.7km離れたカフェまで自転車で往復した。行きは上り坂で平均時速8.1km/時、帰りは下り坂で平均時速13.5km/時で自転車を漕いだ。また、カフェには45分滞在した。このとき、家を出てから帰宅するまでにかかった時間は何分か求めよ。
【解答&解説】
家からカフェまでにかかった時間は2.7 ÷ 8.1=1/3[時間]=20[分]ですね。
同様に考えて、カフェから家までにかかった時間=2.7 ÷ 13.5=1/5[時間]=12[分]です。
カフェの滞在時間は45分とのことなので、求める答えは20+45+12=77[分]・・・(答)となります。
【練習問題3】
P地点からQ地点までに自転車で往復したところ、行きは45分、帰りは50分かかった。行きの平均時速は時速20kmだったとすると、帰りの平均速度は時速何kmか求めよ。
【解答&解説】
PQ間の距離=20 × 45/60=15[km]であることがわかります。
よって、帰りの平均速度=15 ÷ 50/60=18[km/時]・・・(答)となります。
【練習問題4】
家から学校までは8kmの距離があり、普段は自転車で30分かけて通学している。ある日、家を出るのが5分遅れてしまった。普段と同じ時刻に学校に到着するには平均時速を普段よりどれだけ速くすれば良いか求めよ。
【解答&解説】
普段より5分早い25分で8kmを走行しなければなりません。
このときの速度=8 ÷ 25/60=19.2[km/時]です。
普段の平均速度=8 ÷ 30/60=16[km/時]なので、19.2-16=3.2[km/時]・・・(答)速くする必要があるとわかります。
【練習問題5】
家から4.2km離れた図書館まで最初は4.5km/時で歩いたが、途中から10km/時で走ったので、合計で34分かかった。このとき、歩いていた時間は何分か求めよ。
【解答&解説】
34分=34/60[時間]=17/30[時間]です。
歩いていた時間をa時間とすると、走っていた時間は(17/30 – a)時間となります。
すると、4.5a+10(17/30 – a)=4.2という方程式を立てることができます。
これを解くとa=4/15[時間]となります。
※方程式の解き方がわからない人は「【SPI】方程式はこの2つだけ絶対覚えよう!例題でわかりやすく解説!練習問題付き」をご覧ください。
4/15[時間]=16[分]なので、答えは16分・・・(答)となります。
【練習問題6】
A君は自宅から学校まで普段は平均時速4.5km/時で歩いて通っているが、ある日、普段の80%のスピードが歩いたところ、普段より5分遅れて学校に到着した。A君は普段学校まで何分かかっているか求めよ。
【解答&解説】
A君の普段の通学時間をa時間とすると、自宅から学校までの距離は4.5a[km]となります。
すると、以下の方程式が成り立ちます。
4.5a=4.5×0.8×(a+5/60)
これを解くとa=1/3となります。1/3時間=20分なので、答えは20分・・・(答)です。
【練習問題7】
長さ200mの電車が時速72kmで800mのトンネルを通過する。このとき、電車がトンネルを通過するのに何秒かかるか求めよ。
【解答&解説】
電車の先頭がトンネルに入ってから、電車の末尾がトンネルの出口を出るまで、電車が進む距離は200+800=1000[m]です。
時速72km=秒速20mなので、求める答えは1000÷20=50[秒]・・・(答)となります。
【練習問題8】
時速72kmの電車Aの後ろを、時速108kmの電車Bが並行して走っている。電車Aの長さは200m、電車Bの長さは240mである。電車Bが電車Aに追いついてから追い越すまでに何秒かかるか求めよ。
【解答&解説】
電車Aと電車Bの速度差は108-72=36[km/時]ですね。
これを秒速に変換すると、10m/秒となります。
電車Bの移動距離は200+240=440[m]です。
よって求める答えは440÷10=44[秒]・・・(答)となります。
【練習問題9】
時速102kmの急行列車と時速60kmの普通列車がすれちがう。急行列車の長さが200m、普通列車の長さが160mのとき、2つの列車が完全にすれちがうのに何秒かかるか求めよ。
【解答&解説】
急行列車と普通列車の速度の合計は102+60=162[km/時]ですね。
これを秒速に変換すると45m/秒です。
急行列車の移動距離は160+200=360[m]です。
よって求める答えは360÷45=8[秒]・・・(答)となります。
【練習問題10】
AとBの2人がP地点からQ地点までを一緒に走る。P地点からQ地点までは14kmある。Aは時速9km、Bは時速12kmで走るものとする。Aがスタートしてから10分後にBがスタートする場合、BがAに追いつくのはAがスタートしてから何分後か求めよ。
【解答&解説】
Aは10分、すなわち1/6[時間]でBとの間に9 × 1/6=1.5[km]の距離を空けていることがわかります。
AとBの速度差は3[km/時]なので、BがAに追いつくのは15÷3=0.5[時間]=30[分後]であることがわかります。
問題は「Aがスタートしてから何分後か」なので、答えは30+10=40[分後]・・・(答)となります。
【練習問題11】
28km離れたA地点とB地点がある。Pは時速5kmでA地点からB地点に向かって、Qは時速7kmでB地点からA地点に向かって歩き始めた。PとQが同時に出発した場合、2人が出会うのは出発してから何時間何分後か求めよ。
【解答&解説】
2人が出会うまでの時間をa時間とおきます。
すると、Pの移動距離は5a[km]、Qの移動距離は7a[km]です。この合計は28kmになるので、
5a+7a=28より、a=7/3が求まります。
7/3[時間]=2時間20分・・・(答)となります。
【練習問題12】
1周7kmの池の周りをRは時速13km、Sは時速18kmの自転車で走る。今、RとSは同じスタート時点にいて、2人の速度は常に一定であるものとする。Sがスタートした15分後にRが同じ方向に向かって走り出した場合、Sが最初にRを追い越すのはSがスタートしてから何分後か求めよ。
【解答&解説】
SがRに追いつくとき、Sが走る距離はRが走る距離よりも1周多くなることに注目します。
Sの走行時間をa時間とすると、Rの走行時間は15(=0.25時間)短いので(a-0.25)時間となります。
すると、
18a=13×(a-0.25)+7という方程式が立てられます。
これを解くとa=0.75[時間]となります。0.75時間=45分・・・(答)となります。
【練習問題13】
P地点とQ地点は2.8km離れている。AはP地点を9:20に出発してQ地点に向かい、BはQ地点を9:30に出発してP地点に向かったところ、2人は9:40にすれ違った。BがAの1.5倍の速度で歩いているとすると、Aの平均時速は時速何kmか求めよ。
【解答&解説】
2人がすれ違うのはAが出発してから20分後(=1/3時間後)、Bが出発してから10分後(=1/6時間後)です。
Aの平均時速をa[km/時]とおくと、
- Aが歩いた距離=a/3[km]
- Bが歩いた距離=1.5a × 1/6=a/4[km]
であることがわかります。
この合計は2.8kmになるので、a/3 + a/4=2.8という方程式が成り立ちます。
これを解くとa=4.8[km/時]・・・(答)となります。
【練習問題14】
家から学校まで30km離れている。家から駅まで平均時速20kmの自転車で行き、駅から電車に乗って学校に行くと、自宅から学校まで45分かかった。ただし、駅から学校までの平均時速は50kmで、電車の停止時間や乗り継ぎにかかる時間は考えないものとする。このとき、駅から学校までの距離を求めよ。
【解答&解説】
家から学校までの所要時間は45分=0.75時間です。
家から駅までの所要時間をa時間とすると、駅から学校までの所要時間は(0.75-a)時間となります。
家から学校までの距離は30kmなので、
20a+(0.75-a)×50=30
という方程式が成り立ちます。
これを解くとa=0.25[時間]=15[分]となります。
すると、駅から学校までの所要時間は45-15=30[分]=0.5[時間]とわかります。
よって求める答えは50×0.5=25[km]・・・(答)となります。
【練習問題15】
AとBの2人が同じウォーキングコースを歩く。Aはスタート地点を10:30に出発し、Bは同じスタート地点を10:45に出発したところ、11:30にAを追い抜いた。Aの速度が時速7.2kmだとすると、Bの速度は時速何kmか求めよ。
【解答&解説】
BがAを追い越すのはAが出発してから1時間後なので、Aの進んだ距離は7.2×1=7.2[km]です。
Bはこの距離を11:30 – 10:45=45分=0.75時間が進みます。
つまり、Bの平均時速は7.2÷0.75=9.6[km/時]・・・(答)となります。
【練習問題16】
家から1.6kmはなれた学校まで行くのに、4.8km/時の速さで歩くと始業時間に3分遅れることがわかっている。始業時間の2分前に到着するためには、時速何kmで歩けばよいか求めよ。
【解答&解説】
1.6kmを4.8km/時の速さで歩くと1.6÷4.8=1/3時間=20分かかることがわかります。
始業時間の2分前に到着するためには、家から学校まで20-3-2=15分で行かなくてはなりません。
15分=1/4時間です。よって求める速度は1.6 ÷ 1/4=6.4km/時・・・(答)となります。
【練習問題17】
A君は2.7km/時で、B君は3.6km/時の速度で歩くものとする。A君は家から図書館まで歩いて42分かかるものとする。このとき、以下の問いに答えよ。
(1)A君は家から図書館に向かって、B君は図書館から家に向かって同時に歩き始めたとき、2人が出会うのは何分後か求めよ。
(2)A君が家から図書館に向かって歩き始めた5分後にB君がA君の後を追って家を出た。このとき、B君は何分後にA君に追いつくか求めよ。
【解答&解説】
(1)42分=42/60時間=7/10時間なので、家から図書館までの距離=2.7×7/10=1.89kmであることがわかります。
また、2.7km/時間=0.045km/分、3.6km/時=0.06km/分です。
A君は家から図書館に向かって、B君は図書館から家に向かって同時に歩き始めたとき、1分ごとに0.045+0.06=0.105[km]ずつ距離が縮まるので、答えは1.89÷0.105=18[分]・・・(答)となります。
(2)A君が家から図書館に向かって歩き始めてから5分間でA君が進んだ距離=0.045×5=0.225[km]です。
B君がA君の後を追うとき、1分ごとに0.06-0.045=0.015[km]ずつ距離が縮まるので、答えは0.225÷0.015=15[分]・・・(答)となります。
【練習問題18】
3km/時で進む歩くエスカレーター(以下画像)の上を2.4km/時で歩いたら、歩くエスカレーターに乗ってから40秒で降りることになった。この歩くエスカレーターの長さは何mか求めよ。
【解答&解説】
3km/時で進む歩くエスカレーターの上を2.4km/時で歩いたので、実際の速度は3+2.4=5.4[km/時]となります。
5.4km/時=1.5m/秒です。
1.5m/秒で40秒進んだので、求める距離(=歩くエスカレーターの長さ)=1.5×40=60[m]・・・(答)となります。
🔽 本にも載ってない極秘情報 🔽
速度算の練習問題は以上となります。
速度算はSPIの非言語(数学)で出題頻度が高いかつ難易度もそこまで高くはないので、対策のコスパは非常に良い分野です。
ぜひ優先度を高めていただければと思います。


