
SPIの非言語(数学)では不等式に関する知識が必須です。
※SPIの非言語(数学)を完全解説した記事もぜひ参考にしてください。
しかし、SPIを受検予定の就活生や転職活動中の社会人の中には不等式の解き方などを忘れてしまった人もいるでしょう。
本記事では不等式とは何かや不等式の解き方について解説した後、SPIで出題される不等式の問題例をご紹介していきます。
ちなみにですが、SPIにはたった3時間の勉強でSPIが通過してしまう勉強法があります。
これさえあれば限りなく少ない努力で内定に大きく近づきます。
これは私が100回以上ものSPI受検を通して生み出した、どの本にも載っていない超コスパの良い究極の勉強法です。
興味のある人はぜひ以下のボタンからその方法をチェックしてみてください。
【SPI】不等式とは?不等号って何?
不等式とは不等号を用いた式のことです。
不等号とは2つ以上の数字を比較したとき、どちらが大きいか小さいかを示すための記号です。
不等号には「<」「>」「≦」「≧」の4つがあります。
「<」は「小なり」と読み、「a<b」のように記載します。
※「a<b」が不等式となりなます。
「a<b」は「aはbよりも小さい(aはb未満)」を表しています。
「>」は「大なり」と読み、「a>b」のように記載します。「a>b」は「aはbよりも大きい」を表しています。
「≦」は「小なりイコール」と読み、「a≦b」のように記載します。「a≦b」は「aはb以下である」を表しています。
「以下」なので、a=bでも問題ありません。
「≧」は「大なりイコール」と読み、「a≧b」にように記載します。「a≧b」は「aはb以上である」を表しています。
「以上」なので、先ほどの「≦」と同様にa=bでも問題ありません。
【SPI】不等式の解き方
不等式には一次不等式や二次不等式など様々な不等式がありますが、SPIの非言語で必要なのは一次不等式のみです。
一次不等式は「a+4<10」や「X-9≧5」などのことです。
一次不等式の解き方は簡単です。
aやxなどの文字を左側(左辺)に、10や4などの数字を右側︎(右辺)に移行させればよいです。
1つ例題を解いてみましょう。
【例題】
以下の一次不等式を解きなさい。
(1)x+10<35
(2)2a-5≧19
【解答&解説】
(1)左辺を文字だけの不等式にすると、x<25・・・(答)となります。
(2)不等号が「≧」になってもやることは変わりません。
まずは左辺を文字だけの不等式にすると、2a≧24となりますね。
両辺を2で割って、a≧12・・・(答)が正解です。
【SPI】不等号の向きが変わるケースに注意
不等式では両辺にマイナスの数を掛けたり、マイナスの数で割ったりすると不等号の向きが変わります。
例えば、-2a<30という不等式を解いてみます。
左辺をaだけにするには両辺を-2で割ればよいので、a<-15が答えになると思う人が多いですが、それは間違いです。
a<-15だと、例えばa=-100があてはまりますが、a=-100を-2a<30に代入すると200<30となり、不等式が成り立ちません。
正解は不等号の向きが変わって、a>-15となります。
以上の法則は必ず覚えておきましょう。
🔽 本にも載ってない極秘情報 🔽
SPIで出題される不等式の問題例
SPIの非言語では先ほどご紹介したような「a+4>10を解きなさい」といった問題は出題されません。
正解を導く過程で不等式が必要な問題が出題されます。問題例は以下の通りです。
【例題】
1個110円のチョコと1個80円のガムを合わせて50個買うことにした。代金の合計を5000円以下にする場合、チョコは最大で何個買うことができるか求めよ。
【解答&解説】
チョコをa個買う場合、ガムは(50-a)個買うことになります。
このときの代金の合計は110a+80(50-a)=(30a+4000)円となりますね。
よって、30a+4000≦5000という不等式を立てることができます。
両辺から4000を引くと、30a≦1000となるので、a≦33.33・・・となります。
aはチョコの個数で明かに整数なので、aの最大値は33[個]・・・(答)となります。
SPIのグラフの領域問題では不等式が必ず出る!
ペーパーテスト型のSPIではグラフの領域という問題が出題範囲に含まれています。
※SPIのペーパーテスト(筆記試験・マークシート)を完全解説した記事もぜひ参考にしてください。
グラフの領域問題では不等式が必ず登場しますのでご注意ください。
問題例は以下の通りです。
【例題】
次の不等式が同時に成り立つ領域は以下の図のA〜Iの中のどれか答えよ。
- x<0
- 0<y<2
- y>x-1
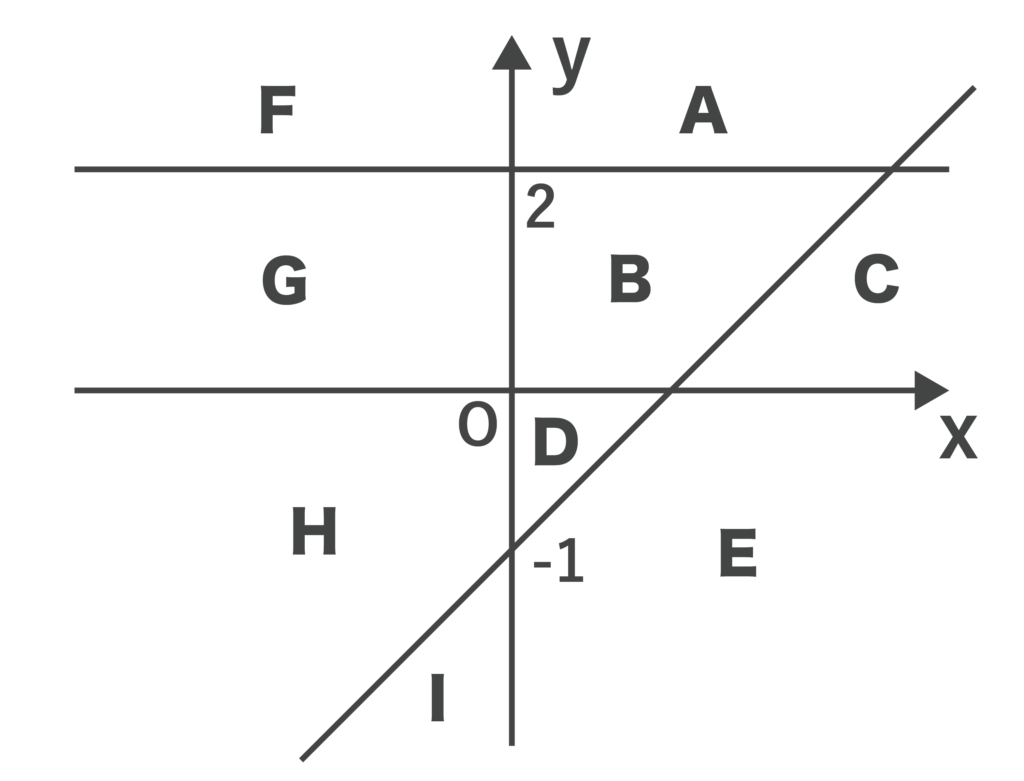
【答え】
答えはGです。なぜGになるのかわからない人は「SPIのグラフの領域を例題でわかりやすく解説!対策優先度は低い?」をご覧ください。
🔽 本にも載ってない極秘情報 🔽
今回はSPIと不等式の関係について解説していきました。
不等式は数学の基本です。必ず理解しておきましょう!


