
旅人算はSPIで出題されるので、SPIで高得点を狙っている人は特にしっかりと対策をしておきましょう。
SPIで出題される旅人算の難易度は高くないので、得点にも繋げやすいです。
本記事ではSPIの受検回数100回を超えるSPIマスターの私カズマがSPIの旅人算の解き方やコツについて例題でわかりやすく解説していきます。
SPIを受検予定の就活生や転職活動中の社会人はぜひ最後までご覧ください。
ちなみにですが、SPIにはたった3時間の勉強でSPIが通過してしまう勉強法があります。
これさえあれば限りなく少ない努力で内定に大きく近づきます。
これは私が100回以上ものSPI受検を通して生み出した、どの本にも載っていない超コスパの良い究極の勉強法です。
興味のある人はぜひ以下のボタンからその方法をチェックしてみてください。
旅人算とは?SPIでの出題頻度や難しさは?
旅人算とは2人の人間が出会ったりすれ違ったりするまでの時間や道のりなどを求める問題です。
旅人算は小学校の算数(数学)で習う内容で、SPIの非言語の出題範囲にも含まれています。
※SPIの非言語(数学)を完全解説した記事もぜひ合わせてご覧ください。
SPIで出題される旅人算の難易度は易しいのでご安心ください。しっかりと対策をすれば確実に得点に繋げられる分野です。
出題頻度に関してですが、WEBテスティングにおいては旅人算はほとんど出題されません。
※SPIのWEBテスティングとは何かについて完全解説した記事もぜひ参考にしてください。
なので、WEBテスティング型のSPIを受検予定の人は旅人算の対策優先度を高める必要はないでしょう。
しかし、テストセンターではそこそこの頻度で出題されるので、対策優先度を高めることをおすすめします。
※SPIのテストセンターとは何かについて解説した記事もぜひ合わせてご覧ください。
【SPI】旅人算で覚えることは2つだけ!例題でわかりやすく解説
旅人算では「追いつく」パターンと「出会う」パターンの2つがあります。
それぞれの解き方・コツについて例題で解説していきます。
「追いつく」パターン
1人の人間がもう1人の人間を追いかけたとき、追いつくのにかかる時間などを求める問題です。
【例題】
妹は7時に家を出発して80m/分の速さで学校に向かった。その5分後に兄が家を出て100m/分の速さで妹を追いかけた。兄が妹に追いつく時刻は何時何分か求めよ。
【解答&解説】
妹の速さは80m/分なので、5分間で80×5=400[m]進みます。
※距離=速さ×時間で求められるのでした。詳しくは「【SPI】速度算の練習問題18問!コツや解き方・公式・計算方法を完全解説!」をご覧ください。
つまり、7時5分時点の状況は以下のようになります(兄と妹の間の距離は400mとなります)
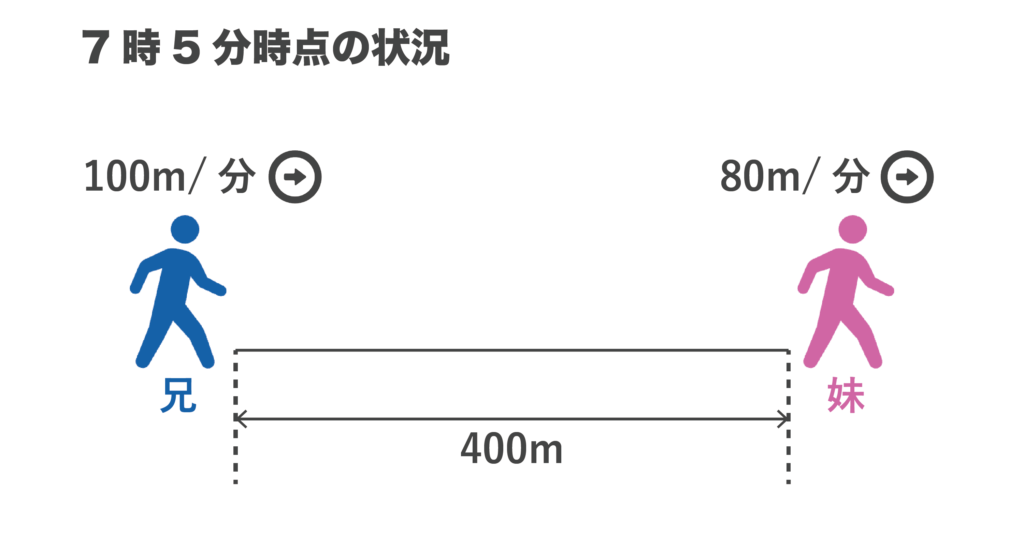
妹の速さは80m/分、兄の速さは100m/分の速さなので、1分間で20m(100-80より)ずつ距離が縮まることになります。
よって兄が妹に追いつくのは兄が家を出発してから400÷20=20[分後]であることがわかります。
兄が家を出たのは妹が家を出てから5分後なので、その時刻は7時5分です。
よって答えは7時5分の20分後となるので、7時25分・・・(答)となります。
「追いつく」パターンの旅人算では2人の速さの差に注目するようにしましょう。
「出会う」パターン
離れた場所にいる2人の人間が出会うまでにかかる時間などを求める問題です。
【例題】
3000m離れた地点から太郎君と花子ちゃんが向かい合って同時に出発する。太郎君の速さが35m/分、花子ちゃんの速さが25m/分のとき、2人は出発してから何分後に出会うか求めよ。
【解答&解説】
問題文の条件を絵にすると以下のようになりますね。
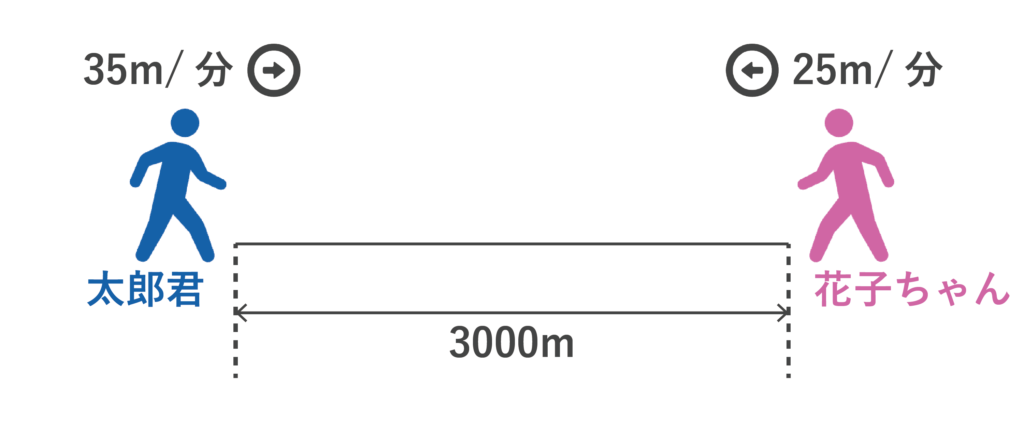
太郎君の速さは35m/分、花子ちゃんの速さは25m/分の速さなので、1分間で60m(35+25より)ずつ距離が縮まることになります。
よって答えは3000÷60=50[分後]・・・(答)となります。
「出会う」パターンの旅人算では2人の速さの和に注目するようにしてください。
【SPI】旅人算の練習問題
最後に旅人算の練習問題をご用意しました。すべて本番のSPIで出題される問題の難易度に近いので、ぜひ解いてみてください。
※SPIの練習問題をたくさん解きたい人はSPIの練習問題433問をすべて無料で掲載している記事もご用意しているので、ぜひご覧ください。
【練習問題】
(1)1800m離れた2地点の両側から向かい合って55m/分のPと65m/分のQが同時に出発した。2人が出会うまでに何分かかるか求めよ。
(2)妹は70m/分で家を出発したが、20分後に姉が100m/分で走って追いかけた。姉は出発してから何分後に妹に追いつくか求めよ。
(3)300m先を60m/分で歩くAを120m/分でBが追いかけると、何分後に追いつくか求めよ。
(4)4.5km離れた2地点の両側からPとQが向かい合って同時に出発したところ、2人は30分で出会った。Pの速さが80m/分だとすると、Qの速さは分速何mか求めよ。
(5)1周4.5kmのマラソンコースを80m/分の甲と、70m/分の乙が同時に同じ地点から反対向きに進んだ。2人が3回目に出会うのは出発してから何分後か求めよ。
(6)Pは80m/分で家から公園へ、Qは50m/分で公園から家へ向かって同時に出発したところ、2地点のちょうど真ん中より120m離れた地点で出会った。家と公園の距離は何mか求めよ。
(7)ある池を1周するのにAは6分、Qは12分かかる。2人が同じところから同時に反対の方向に歩きだすと、2人が出会うまでに何分かかるか求めよ。
(8)甲と乙は1000m離れている。2人が同時に向かい合って歩き始めると、5分後に2人の距離は400mになった。あと何分何秒で2人は出会うか求めよ。
【解答&解説】
(1)1800÷(55+65)=1800÷120=15[分]・・・(答)
(2)(70×20)÷(100-70)=1400÷40=35[分後]・・・(答)
(3)300÷(120-60)=300÷60=5[分後]・・・(答)
(4)4.5km=4500mです。Qの速さをa[m/分]とおきます。
すると4500÷(80+a)=30という一次方程式が立てられるので、80+a=4500÷30=150となるので、a=70[m/分]・・・(答)となります。
※一次方程式の解き方がわからない人は「【SPI】方程式はこの2つだけ絶対覚えよう!例題でわかりやすく解説!練習問題付き」をご覧ください。
(5)1回出会った後、次に出会うまでに2人が進んだ距離の和は1周分の4500mなので、4500÷(80+70)=30[分]です。
これを3周繰り返しているので、答えは30×3=90[分]・・・(答)となります。
(6)Pは真ん中より120m多く、Qは120m少なく歩いたので、2人が歩いた距離の差は240mとなります。
PとQは毎分30m(80-50より)の差がつくので、PとQが出会うまでの時間は240÷30=8[分]です。
よって答えは(80+50)×8=1040[m]・・・(答)となります。
(7)池の周りの長さを2人の時間の最小公倍数である12とおきます。
すると、Aの速さは12÷6=2、Bの速さは12÷12=1となります。
よって答えは12÷(2+1)=4[分]・・・(答)となります。
(8)(1000-400)÷5=120[m/分]となり、これが甲と乙の速さの和になります。
2人の距離はあと400mなので、400÷120=10/3[分]=3分20秒・・・(答)となります。
🔽 本にも載ってない極秘情報 🔽
今回はSPIの旅人算を取り上げました。
「追いつく」パターンでは2人の速さの差に、「出会う」パターンでは2人の速さの和に注目することを必ず覚えておきましょう。


