
SPIの非言語(計数・数学)では物流(物の流れ)に関する問題が出題されるケースがあります。
※「SPIとは?対策方法や問題・例題をすべて紹介!適性検査SPIはこれで完璧だ!」もぜひ合わせてご覧ください。
物流(物の流れ)に関する問題はかなり特殊な問題なので、本番で慌てないためにも事前に一度は解いておきたいところです。
そこで今回はSPIの物流(物の流れ)とはどんな問題なのか?や解き方についてSPIについて日本トップクラスに熟知している私カズマが例題と図解でわかりやすく解説していきます。
また、SPIにおける物流(物の流れ)の勉強・対策の優先度についても詳しく解説していきます。
SPIを受検予定の就活生や転職活動中の社会人はぜひ参考にしてください。
※「SPIの非言語(数学)を完全解説!対策方法やできない人でも点数を上げる方法!問題もご紹介」もぜひ合わせてご覧ください。
ちなみにですが、SPIにはたった3時間の勉強でSPIが通過してしまう勉強法があります。
これさえあれば限りなく少ない努力で内定に大きく近づきます。
これは私が100回以上ものSPI受検を通して生み出した、どの本にも載っていない超コスパの良い究極の勉強法です。
興味のある人はぜひ以下のボタンからその方法をチェックしてみてください。
SPIの物流(物の流れ)はどんな問題?
SPIで出題される物流(物の流れ)の問題は、ある経路を通る人や物の流れを式や図で示していく問題です。
後ほど詳しく解説しますが、物流(物の流れ)はペーパーテストでのみ出題されます。
問題の難易度としては中くらいです。
※「SPIは難しい?難しすぎる?難易度(レベル)を言語と非言語別に解説!苦手・苦手すぎる人がやるべきことは?」もぜひ参考にしてください。
WEBテスティング、テストセンター、インハウスCBTで出題されないので勉強・対策は不要です。
では、SPIで出題される物流(物の流れ)の例題を1問解いてみましょう。
※SPIの練習問題433問をすべて無料で掲載している記事もぜひ参考にしてください。
【例題】
ある業者Pが出荷する商品のうち、比率にしてaが業者Qに納品されることを以下のような図で示すことにする。
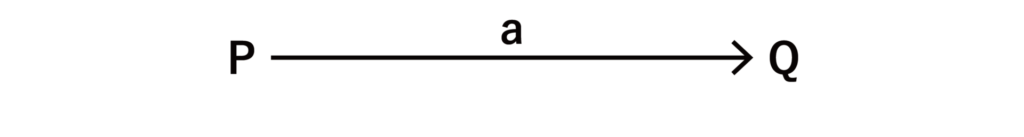
このとき、業者PとQが保有する商品の量をそれぞれP、QとするとQ=aPが成り立つものとする。
また、業者Pが出荷する商品のうち比率aと、業者Qが出荷する商品のうち比率bとが業者Rに納品されることを以下のような図で示すことにする。
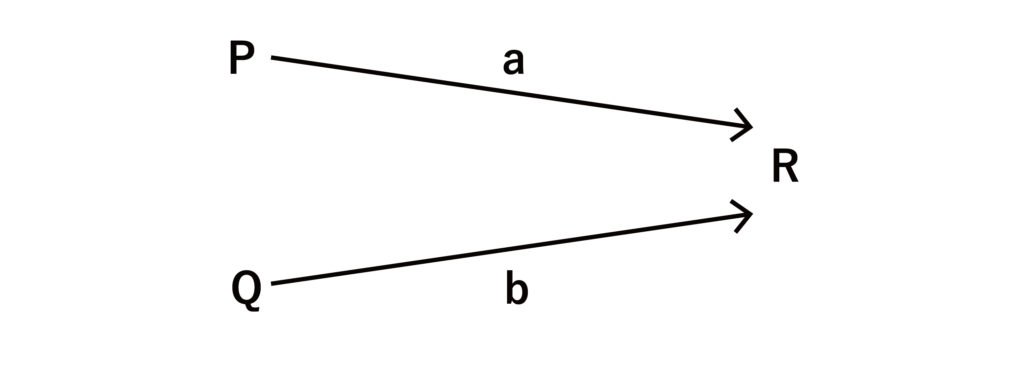
このとき、業者P、Q、Rが保有する商品の量をそれぞれP、Q、RとするとR=aP+bQが成り立つものとする。
また、業者Pが出荷する商品のうち比率aが業者Qを経由し、そのうちの比率にしてbが業者Rに納品されることを以下のような図で示すことにする。
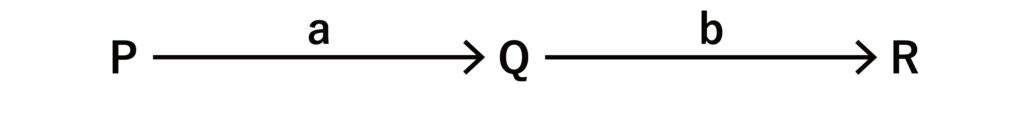
このとき、R=bQが成り立つものとする。また、R=b(aP)=abPとも表すことができるものとする。
このとき、以下の問に答えよ。
(1)以下の図において、業者Tに納品される商品の個数をa、b、c、d、eのすべてを使って式で表現せよ。
(2)以下の図におけるそれぞれの比率がa=0.1、b=0.5、c=0.4、d=0.3、e=0.5であるとき、業者Pが出荷する商品の個数が業者Qが出荷する商品の個数の2倍だとすると、業者Rから業者Tに納品される商品の個数は業者Sから業者Tに納品される商品の個数の何倍か求めよ。
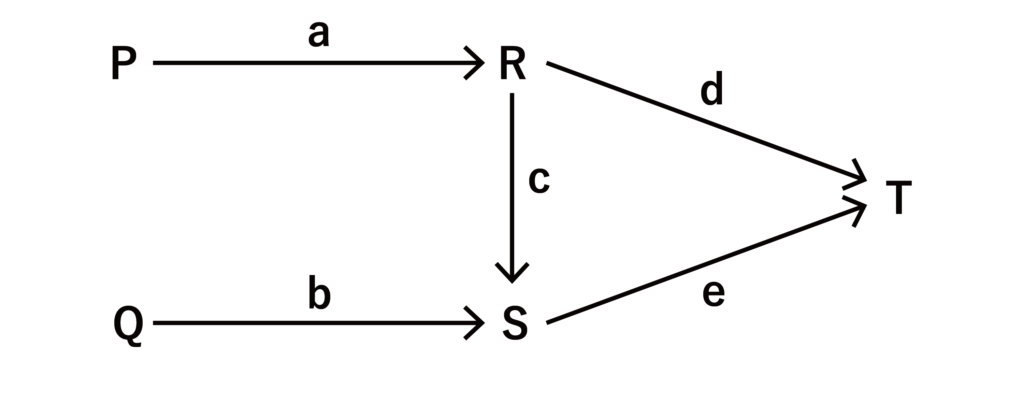
類題:オフィス海(2023). SPI&テストセンター超実戦問題集 株式会社ナツメ社
【解答&解説】
(1)1つずつ順番に見ていきましょう。
まず。PからRにはaP[個]が納品されますね。つまり、R=aPです。
SはQとRの2社から納品されます。よって、SにはbQ+cR=bQ+c(aP)=bQ+acP[個]が納品されます。
そして、TはRとSの社から納品されます。
よって、TにはdR+eS=d(aP)+e(bQ+acP)=adP+beQ+aceP・・・(答)となります。
※確かにa、b、c、d、eのすべての文字が入っていることが確認できます。
(2)業者Pが出荷する商品の個数が業者Qが出荷する商品の個数の2倍であると問題文に書かれているので、今回はPが出荷する商品の個数=200、Qが出荷する商品の個数=100とおいてみましょう。
すると、Rには200×0.1=20[個]がPから納品されます。そして、そのうちの0.3がTに納品されるので、その個数=20×0.3=6[個]となります。
また、Sには
- Qから100×0.5=50[個]
- Rから20×0.4=8[個]
の合計58個が納品されますね。そして、そのうちの0.5がTに納品されるので、その個数=58×0.5=29[個]となります。
よってRからTに納品される商品の個数はSからTに納品される商品の個数の6/29[倍]・・・(答)であることがわかります(6÷29より)
🔽 本にも載ってない極秘情報 🔽
【SPI】物流(物の流れ)の解き方のコツ
SPIで出題される物流(物の流れ)の問題のイメージが掴めたところで、ここからは物流(物の流れ)の解き方のコツについて解説していきます。
解き方のコツとしては、具体的な数値に置き換えれそうな箇所は自分で勝手に適当な数値にしてみることです。
物流(物の流れ)の問題においては、先ほどの例題の(2)ように多くの文字や比率が登場することが多いです。
文字を使ってももちろん解くことはできるのですが、文字だけだとどうしても頭の中が混乱しやすくなります。
なので先ほどの例題の(2)では、
- Pが出荷する商品の個数=200
- Qが出荷する商品の個数=100
を勝手に設定したのです。自分で勝手に適当な数字を設定するテクニックは物流(物の流れ)の問題以外でも非常に有効なので、ぜひ使えるようにしておきましょう。
※「【SPI】割合と比の練習問題20問!難しい?公式や解き方・コツもわかりやすく解説!」もぜひ参考にしてください。
【SPI】物流(物の流れ)が出題される受検方式
冒頭でも述べましたが、物流(物の流れ)に関する問題はかなり特殊な問題であり、SPIではペーパーテストでしか出題されません。
※SPIのペーパーテストについて完全解説した記事もぜひ合わせてご覧ください。
SPIにはWEBテスティング、テストセンター、インハウスCBTの4つの受検方式が用意されていますが、ほとんどの企業(推定9割以上)はWEBテスティングもしくはテストセンターを採用しています。
※WEBテスティングは受検期限内に受検者が自分のPCから好きな時間・場所でSPIを受検する方式です。テストセンターは企業が用意した会場にまで受検者が足を運び、その会場に設置されているPCからSPIを受検する方式です。詳しくはSPIのテストセンターとは何かについて詳しく解説した記事をご覧ください。
SPIでペーパーテストを採用している企業はかなり稀であり、物流(物の流れ)に勉強・対策の時間を割くのは非常にもったいないのでご注意ください。
※「SPIの対策方法・勉強法を日本一SPIに詳しい筆者が真剣に考えてみた」もぜひ合わせてご覧ください。
【SPI】物流(物の流れ)の練習問題
最後に、物流(物の流れ)の練習問題をご用意しました。
SPIのペーパーテストを受検予定の就活生や転職活動中の社会人はぜひ解いてみてください。
※「【SPI】転職・中途採用の対策法や問題・通過率などをSPIマスターが完全解説」もぜひ参考にしてください。
【練習問題1】
以下の図は業者Pから業者Sに商品が納品されるまでの流れを示している。a〜dは比率を示しており、式の表記ルールは上記例題と同じであるとする。このとき、以下の問に答えよ。
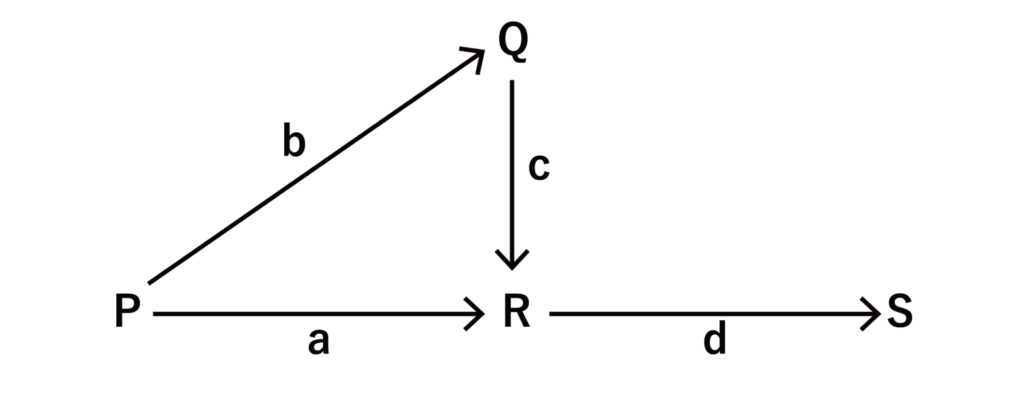
(1)Sに納品される商品の個数をPのみで表せ。
(2)a=0.7、b=0.1、c=0.5、d=0.4としたとき、Pから出荷された商品のうちSに納品される商品は何%か求めよ。
【解答&解説】
(1)まず、PからQにはbP[個]の商品が納品されますね。
そして、そのうちの割合にしてcがQからRに納品されるので、QからRに納品される商品の個数=cQ=c×bP=bcP[個]です。
また、RはPからもaP[個]納品されるので、Rには全部でaP+bcP[個]の商品が納品されます。
そのうち、比率にしてdがSに納品されるので、S=dR=d(aP+bcP)=adP+bcdP[個]・・・(答)となります。
(2)Pに100個の商品があるとしましょう。
すると、Qに100×0.1=10[個]がPから納品されます。そして、そのうちの0.5がRに納品されるのでRはQから10×0.5=5[個]納品されます。
また、RはPからも100×0.7=70[個]納品されるので、全部で70+5=75[個]納品されます。
そして、そのうちの0.4がSに納品されるので、Sには75×0.4=30[個]の商品が納品されます。
Pから出荷された商品=10+70=80[個]なので、答えは30÷80×100=37.5[%]・・・(答)となります。
【練習問題2】
ある展示会において7つのブースP・Q・R・S・T・U・Vを出展した。以下の図におけるa〜gは客数の比率を表しており、a=0.8、b=0.2、c=0.4、d=0.3、e=0.1、f=0.5、g=0.7とする。例えば、以下の図ではブースPに来た客数のうち比率a(=0.8)はブースSに移動することを示している。このとき、以下の問に答えよ。
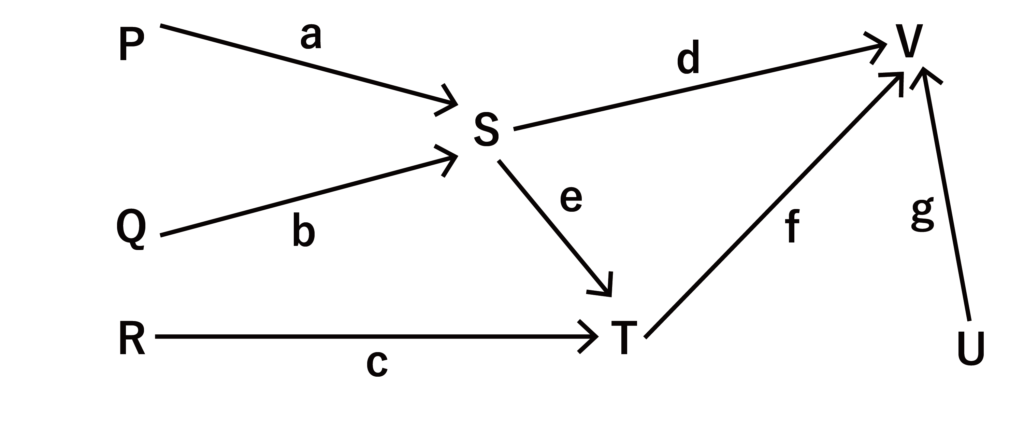
(1)ブースPに来た客数のうち何%がブースVに行っているか求めよ。
(2)ブースPに来た客数が800人、ブースQに来た客数は400人だった。また、ブースSからブースTに移動した客数は、ブースTからブースVに移動した客数より10人多かった。このとき、ブースRの客数を求めよ。
【解答&解説】
(1)ブースPに来た客数=100人としてみましょう。
すると、PからSに行った客数=100×0.8=80[人]ですね。
そして、SからVに行った人=80×0.3=24[人]です。
また、SからTに行った人=80×0.1=8[人]です。そして、TからVに行った人=8×0.5=4[人]です。
よって、Vに行った人は合計で24+4=28[人]であることがわかるので答えは28[%]・・・(答)となります。
(2)PからSに行った人=800×0.8=640[人]ですね。また、QからSに行った人=400×0.2=80[人]です。
よってSには合計で640+80=720[人]の客が来たことがわかります。
このうちTに行ったのは720×0.1=72[人]ですね。
SからTに移動した客数(=72人)は、TからVに移動した客数より10人多かったとのことなので、TからVに移動した人は72-10=62[人]とわかります。
f=0.5なので、T=62÷0.5=124[人]であることがわかります。
TにはSから72人(720×0.1より)が来ているので、RからTに来た人=124-72=52[人]であることがわかります。
よって、Rの客数は52÷0.4=130[人]・・・(答)となります。
🔽 本にも載ってない極秘情報 🔽
いかがでしたでしょうか?
今回はSPIの物流(物の流れ)を取り上げました。本記事を通して物流(物の流れ)の問題のイメージを掴んでいただけたかと思います。
また、今回ご紹介した「適当な数字を自分で勝手に設定する」というテクニックの有効性は練習問題でも十分ご理解いただけたかと思います。ぜひSPIの本番(ペーパーテスト)でも使ってみてください。


