
SPIの非言語では集合問題が出題範囲に含まれていますが、集合問題の解き方はベン図とカルノー表の2つがあります。
※「SPIとは?対策方法や問題・例題をすべて紹介!適性検査SPIはこれで完璧だ!」もぜひ合わせてご覧ください。
今回はカルノー表を使った集合問題の解き方を具体例でわかりやすく解説していきます。
SPIを受検予定の就活生や転職活動中の社会人はぜひ最後までご覧ください。
ちなみにですが、SPIにはたった3時間の勉強でSPIが通過してしまう勉強法があります。
これさえあれば限りなく少ない努力で内定に大きく近づきます。
これは私が100回以上ものSPI受検を通して生み出した、どの本にも載っていない超コスパの良い究極の勉強法です。
興味のある人はぜひ以下のボタンからその方法をチェックしてみてください。
SPIのカルノー表とは?
SPIの非言語の集合問題で出題されるカルノー表はカルノー図とも呼ばれており、以下のような表のことを言います。
※「【SPI】集合・ベン図の練習問題13選!解き方や3つ・少なくとものケースまで網羅」もぜひ参考にしてください。
【カルノー表の例】
| チョコが好き | チョコが嫌い | 合計 | |
|---|---|---|---|
| ケーキが好き | 10人 | 13人 | 23人 |
| ケーキが嫌い | 6人 | 9人 | 15人 |
| 合計 | 16人 | 22人 | 38人 |
上記のカルノー表を使えば、
- チョコもケーキも好きな人=10人
- チョコが好きでケーキが嫌いな人=6人
- チョコが嫌いでケーキが好きな人=13人
- チョコもケーキも嫌いな人=9人
ということが視覚的にわかります。
また、カルノー表では縦の合計と横の合計が等しくなります。
上記のカルノー表だと、縦の合計は23+15=38[人]、横の合計も16+22=38[人]となっています。
【SPI】カルノー表の使い方を例題で解説
では、実際のSPIで出題される集合問題をどうやってカルノー表で解けばよいのでしょうか?
本記事では以下の例題をカルノー表を使って解いてみます。
【例題】
一人暮らしの大学生80人に家電製品についてアンケート調査を行った。以下はその調査結果である。
- 電子レンジを持っている=59人
- 電子レンジを持っていない=21人
- 洗濯機を持っている=44人
- 洗濯機を持っていない=36人
洗濯機を持っている人の1/4が電子レンジを持っていなかったとき、電子レンジを持っている人のうち洗濯機を持っていない人は何人か求めよ。
【解答&解説】
まずは問題文で与えられた4つの条件をもとに以下のようなカルノー表を作ってみます。〇=持っている、×=持っていないを表します。
| 単位:人 | 電子レンジ〇 | 電子レンジ× | 合計 |
|---|---|---|---|
| 洗濯機〇 | X | 44 × 1/4=11 | 44 |
| 洗濯機× | Y | Z | 36 |
| 合計 | 59 | 21 | 80 |
「電子レンジを持っている人のうち洗濯機を持っていない人」は上記のカルノー表のYに該当します。
まずはXを求めます。X=44-11=33であることがわかります。
よって、Y=59-33=26[人]・・・(答)となります。
ちなみに、Z=36-Y=36-26=10です。
電子レンジ×の縦に注目してみると、11+Z=11+10より、確かに21になっていることが確認できます。
🔽 本にも載ってない極秘情報 🔽
ベン図とカルノー表どっちがおすすめ?
上記の集合問題はカルノー表ではなくベン図を使っても解くことができます。
ベン図を使った解き方は以下です。
【別解】
与えられた条件より、以下のベン図を書くことができます。
※以下のベン図の11は「洗濯機を持っている人の1/4が電子レンジを持っていなかった」という条件の44× 1/4=11から記載しています。
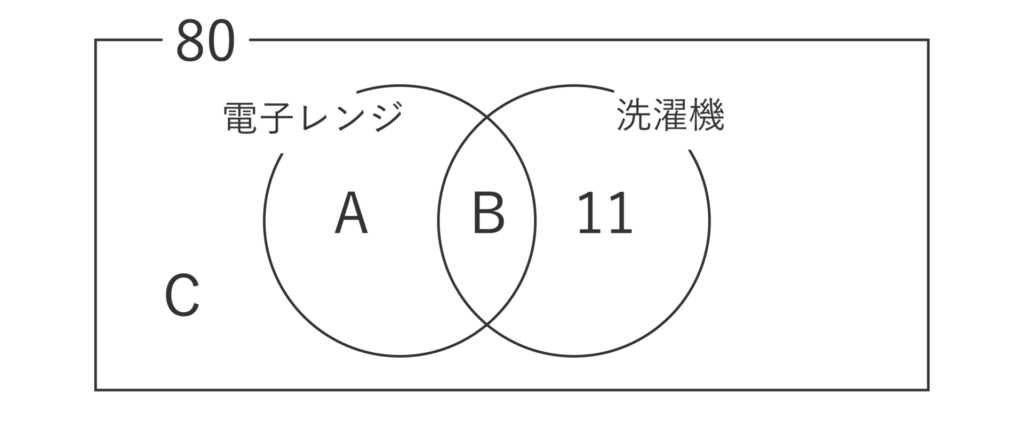
- A=電子レンジを持っているが、洗濯機は持っていない人
- B=電子レンジも洗濯機も両方持っている人
- C=電子レンジも洗濯機も両方持っていない人
を表しています。
今回求めるのは「電子レンジを持っていて洗濯機を持っていない人」なので、上記ベン図のAに該当します。
問題文より、電子レンジを持っている人は59人なので、A+B=59が成り立ちます。
問題文より、洗濯機を持っている人は44人なので、B+11=44が成り立ちます。つまり、B=44-11=33です。
よって、A=59-33=26[人]・・・(答)となります。
ちなみにですが、問題文より、電子レンジを持っていない人は21人なので、C+11=21が成り立ちます。
よって、C=21-11=10です。
集合が2つの場合はベン図よりもカルノー表の方が視覚的にもわかりやすいのでおすすめです。
SPIで集合が3つある場合、カルノー表は使える?
以上でご紹介した例題は集合が2つでしたが、集合が3つある場合でもカルノー表は使えるのでしょうか?
結論から申し上げますと、使えます。しかし、かなり煩雑になってしまうのでおすすめしません。
集合が3つ以上ある場合はカルノー表ではなくベン図を使うことをおすすめします。
集合が3つ登場する例題を1問ご紹介しておきます。
【例題】
100人を対象に漫画P、Q、Rについて調査したところ、Pは27人、Qは24人、Rは43人が読んでいた。また、PとRの両方を読んだ人は14人、QとRの両方を読んだ人は9人で、PとQの両方を読んだ人はいなかった。このとき、P、Q、Rのいずれも読んでいない人は何人いたか求めよ。
【解答&解説】
各漫画を読んだ人数を足し、複数冊を読んだ人(ダブり)を除きます。
これを対象者100人から引けば、いずれも読んでいない人数がわかります。
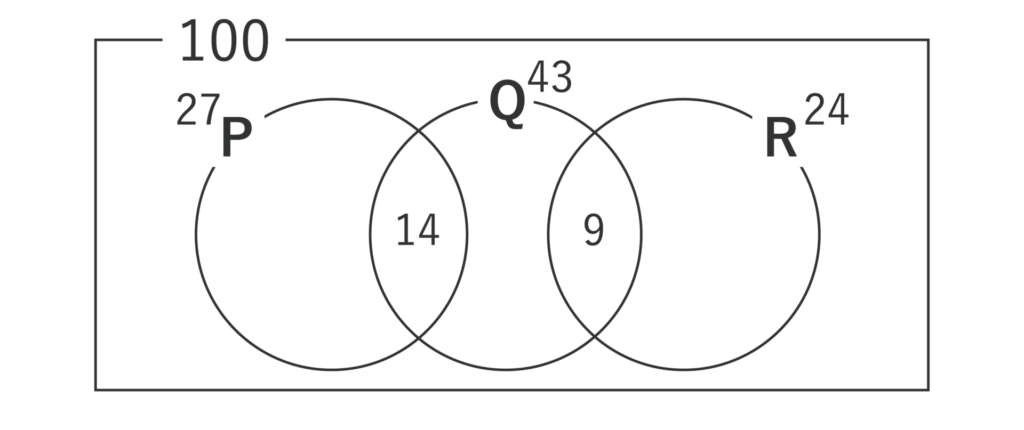
よって、答えは100-(27+24+43-14-9)=29[人]・・・(答)となります。
【SPI】カルノー表の練習問題
最後に、集合の練習問題を1つ用意しました。ぜひカルノー表を使って解いてみてください。
※SPIの練習問題433問をすべて無料で掲載している記事もぜひ合わせてご覧ください。
【練習問題】
大学生1200人に対して、行ったことのある国に関するアンケートを取ったところ、以下のような結果を得た。
- カナダに行ったことがある:はい=660人、いいえ=540人
- ベトナムに行ったことがある:はい=420人、いいえ=780人
- フランスに行ったことがある:はい=570人、いいえ=630人
(1)カナダとベトナムの両方に行ったことがあると答えた人が145人いた。このとき、カナダにもベトナムにも行ったことがないと答えた人は何人いるか。
(2)カナダに行ったことがないと答えた人のうち、1/3はフランスに行ったことがあると答えた。このとき、カナダとフランスの両方に行ったことがあると答えた人は何人いるか。
【解答&解説】
(1)以下のようなカルノー表を作ります。
| ベトナム〇 | ベトナム× | 合計 | |
|---|---|---|---|
| カナダ〇 | 145 | X | 660 |
| カナダ× | Y | 540 | |
| 合計 | 420 | 780 |
カナダにもベトナムにも行ったことがない人は上記のカルノー表のYに該当します。
X=660-145=515です。よって、Y=780-515=265[人]・・・(答)となります。
(2)以下のようなカルノー表を作ります。
| フランス〇 | フランス× | 合計 | |
|---|---|---|---|
| カナダ〇 | A | 660 | |
| カナダ× | 540 × 1/3=180 | 540 | |
| 合計 | 570 | 630 |
カナダとフランスの両方に行ったことがある人は上記のカルノー表のAに該当します。
A=570-180=390[人]・・・(答)となります。
🔽 本にも載ってない極秘情報 🔽
今回はSPIで登場するカルノー表とは何か・使い方について解説していきました。
カルノー表は集合が2つの場合は視覚的にわかりやすくて便利なので、ぜひ活用しましょう!


