
SPIの非言語(数学・計数)では総当たり戦に関する問題が出題される場合があります。
後ほど詳しく解説しますが、SPIで総当たり戦の問題が出題されるのは基本的にテストセンターかペーパーテストです。
※SPIのペーパーテストについて完全解説した記事もぜひ合わせてご覧ください。
なので、WEBテスティング・インハウスCBTの受検方式でSPIを受検予定の就活生や転職活動中の社会人は総当たり戦の勉強・対策はしなくても良いでしょう。
本記事ではSPIについて日本トップレベルに詳しいSPIマスターの私カズマが、SPIの総当たり戦とはそもそも何かについて解説した後、総当たり戦の問題を解くコツなどについても解説していきます。
最後には総当たり戦に関する練習問題もご用意しているので、ぜひ最後までご覧ください。
ちなみにですが、SPIにはたった3時間の勉強でSPIが通過してしまう勉強法があります。
これさえあれば限りなく少ない努力で内定に大きく近づきます。
これは私が100回以上ものSPI受検を通して生み出した、どの本にも載っていない超コスパの良い究極の勉強法です。
興味のある人はぜひ以下のボタンからその方法をチェックしてみてください。
SPIの総当たり戦とは?例題で解説
総当たり戦とは全ての人・チームが全ての相手と必ず対戦を行う試合方式のことです。
トーナメント戦とどう違うのか?という疑問がよくありますが、トーナメント戦では戦わない相手もいるのがポイントです。
例えば、以下のトーナメントではAが勝ち進んでいったとしてもEが1回戦で負けてしまえばAとEが戦うことはありません。
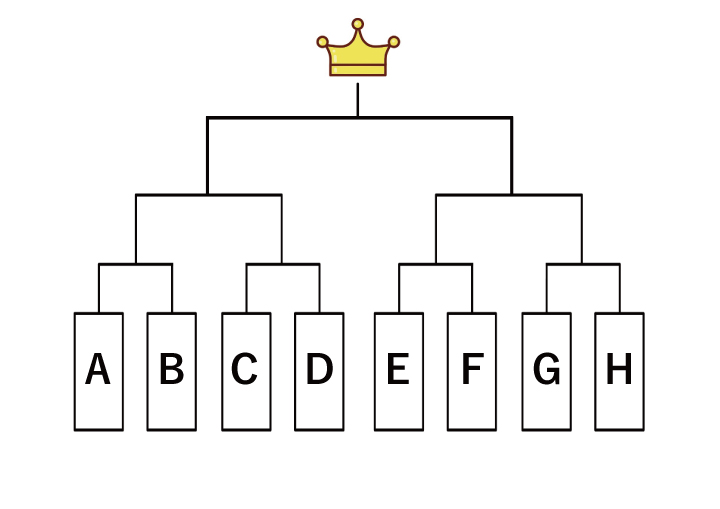
総当たり戦は必ず全員と戦うところがポイントです。
SPIでは総当たり戦に関して以下のような問題が出題されます。
【例題】
4つのチームA・B・C・Dが引き分けのない総当たり戦を行った。これについて以下3つの発言があった。
- P:全敗したチームがある
- Q:全勝したチームは1つもない
- R:勝った数が同じのチームがある
ただし、以上3つの発言は全て信頼できるとは限らない。このとき、正しいものを以下から1つ選びなさい。
- Pが正しければQは必ず正しい
- Qが正しければRは必ず正しい
- Rが正しければPは必ず正しい
【解答&解説】
4チームの総当たり戦なので、以下の通り各チーム3試合ずつ行うことがわかります。
| A | B | C | D | |
|---|---|---|---|---|
| A | ー | |||
| B | ー | |||
| C | ー | |||
| D | ー |
Qの言う通り、全勝(=3勝)したチームが1つもないのであれば全てのチームは0勝・1勝・2勝のどれかになりますね。
チームは全部で4チームあり、0勝・1勝・2勝は3パターンなので、勝った数が同じのチームが必ず登場することになります。
よって答えは「Qが正しければRは必ず正しい」となります。
【補足】
「Pが正しければQは必ず正しい」について調べてみましょう。
「P:全敗したチームがある」ということなので以下のようにAが全敗したとしましょう。
※総当たり戦の対戦表では横(行)のチームから見て縦(列)のチームに勝ったら○、負けたら×を記載するのが一般的です。
| A | B | C | D | |
|---|---|---|---|---|
| A | ー | × | × | × |
| B | ○ | ー | ||
| C | ○ | ー | ||
| D | ○ | ー |
すると、以下のように全勝したチーム(今回はB)が出てきても何もおかしくないですね。
| A | B | C | D | |
|---|---|---|---|---|
| A | ー | × | × | × |
| B | ○ | ー | ○ | ○ |
| C | ○ | × | ー | × |
| D | ○ | × | ○ | ー |
よって「Q:全勝したチームは1つもない」は必ず正しいとは言い切れません。
次は「Rが正しければPは必ず正しい」について調べてみます。
「R:勝った数が同じのチームがある」とのことですが、A=1勝2敗、B=1勝2敗だとするとこの時点で「P:全敗したチームがある」は必ず正しいとは言い切れないことがわかります。
SPIの総当たり戦を解くコツ・公式
SPIに限らずですが、総当たり戦の問題を解くコツとしては先ほどの例題のように必ず総当たり戦の対戦表を書くことです。
総当たり戦の問題は頭の中で考えても絶対に混乱してしまいます。表にすることで情報が整理され、問題が解きやすくなります。
先ほども解説しましたが、総当たり戦の対戦表では横(行)のチームから見て縦(列)のチームに勝ったら○、負けたら×を記載するのが一般的です。
例えば、以下の総当たり戦の対戦表では
- チームAはチームBとチームCに勝った
- チームBはチームAに負け、チームCに勝った
- チームCはチームAにもチームBにも負けた
となります。
| チームA | チームB | チームC | |
|---|---|---|---|
| チームA | ー | ○ | ○ |
| チームB | × | ー | ○ |
| チームC | × | × | ー |
総当たり戦の対戦表の見方は知らない人も意外と多いので、これを機にしっかりと見方を理解しておきましょう。
また、n[人]やn[チーム]で総当たり戦を行う場合の試合数はnC2で計算することが可能です。
例えば、先ほどご紹介した例題は4チームの総当たり戦でしたが、この場合の試合数=4C2=(4×3)/(2×1)=6[試合]となります。
※Cは組み合わせを表しています。組み合わせの計算方法を忘れてしまった人はSPIの組み合わせの公式について解説した記事をご覧ください。
以下の対戦表を見ても、確かに6試合であることがわかります(対戦表で「試合」と記載がある部分)
| A | B | C | D | |
|---|---|---|---|---|
| A | ー | 試合 | 試合 | 試合 |
| B | ー | 試合 | 試合 | |
| C | ー | 試合 | ||
| D | ー |
試合なので、Aチーム VS BチームもBチーム VS Aチームも同じとみなします。なので、4P2ではなく4C2という計算になります。
🔽 本にも載ってない極秘情報 🔽
【SPI】総当たり戦が出題される受検方式と難易度
冒頭でも解説しましたが、SPIで総当たり戦の問題が出題されるのは基本的にテストセンターかペーパーテストです。
※SPIのテストセンターとは何かについて詳しく解説した記事もぜひ参考にしてください。
WEBテスティング、インハウスCBTでは出題されません。
そして、SPIで出題される総当たり戦の問題は推論の問題がほとんどです。
推論とは先ほどの例題のように、与えられた数少ない情報から必ず正しいと推論できるものを求める問題です。
推論はSPIの非言語(計数・数学)の問題の中でも難易度はかなり高いです。
特にテストセンターでは総当たり戦だけでなく様々な種類の推論の問題が出題されるので、テストセンターでSPIを受検予定の就活生や転職活動中の社会人は必ず推論の勉強・対策をしておいてください。
※SPIの推論問題の例題とコツについて解説した記事もぜひ合わせてご覧ください。
【SPI】総当たり戦の練習問題
最後に総当たり戦に関する練習問題をご用意しました。推論問題なので、テストセンター、ペーパーテストでSPIを受検予定の人はぜひ解いてみてください。
【練習問題】
P・Q・R・Sの4人がテニスの総当たり戦を行った。結果について以下のことがわかっている。ただし、引き分けはないものとする。
- PはRだけに負けた・・・①
- QはSに勝った・・・②
このとき、以下の問に答えよ。
(1)以下1〜3の中から必ず正しいと言える推論をすべて選びなさい。
- Sが全敗ならRは全勝である
- Qが1勝2敗なら、Sも同じく1勝2敗である
- Rが全勝なら、Qは1勝2敗である
(2)最も少ない情報ですべての勝敗を確定するには、①・②の他にどんな情報があれば良いか。以下1〜3の中から1つ選びなさい。
- Rは2勝1敗である
- Rは1勝2敗である
- Sは1勝2敗である
【解答&解説】
(1)まずは総当たり戦の対戦表を書いてみましょう。
①より、PはRだけに負けたということなのでQとSには勝ったことがわかります。
①と②の情報を対戦表に反映すると以下のようになりますね。
| P | Q | R | S | |
|---|---|---|---|---|
| P | ー | ○ | × | ○ |
| Q | × | ー | ○ | |
| R | ○ | ー | ||
| S | × | × | ー |
まず1の「Sが全敗ならRは全勝である」ですが、上記の対戦表よりSが全敗(=Rに負ける)だとしてもRはQに負ける可能性があるので必ず正しいとは言えないことがわかります。
続いて、2の「Qが1勝2敗なら、Sも同じく1勝2敗である」ですが、Qが1勝2敗ということはQはRに負けるということですね。しかし、SはRに負けて全敗になる可能性もあるので2は必ず正しいとは言えないことがわかります。
最後に3の「Rが全勝なら、Qは1勝2敗である」ですが、Rが全勝ということはRはQに勝っています。
つまり、QはRに負けています。すると、上記の対戦表よりQは1勝2敗となることがわかるので3は必ず正しいと言えます。よって答えは3「Rが全勝なら、Qは1勝2敗である」のみとなります。
(2)1の「Rは2勝1敗である」に関してですが、現状RはPに勝ったことだけがわかっており、Rを2勝1敗にするためにはQかSどちらかに勝たなくてはいけません。
この時点ですべての勝敗を確定することができないので1は不適となります。
2の「Rは1勝2敗である」ですが、上記の通りRはPに勝ったことだけがわかっているためRを1勝2敗にするにはRがQにもSにも負ければ良いことがわかります。
それを、対戦表に反映すると以下のようになるので、2があればすべての勝敗を確定できることがわかります。
| P | Q | R | S | |
|---|---|---|---|---|
| P | ー | ○ | × | ○ |
| Q | × | ー | ○ | ○ |
| R | ○ | × | ー | × |
| S | × | × | ○ | ー |
最後に3の「Sは1勝2敗である」ですが、Sは現状PとQに負けていることがわかっているので、Sを1勝2敗にするにはSがRに勝てば良いことがわかります。
しかし、それだけだとQとRの対戦結果が不明なので、3は不適となります。
よって答えは2の「Rは1勝2敗である」となります。
🔽 本にも載ってない極秘情報 🔽
いかがでしたか?
今回はSPIの総当たり戦の問題や解き方のコツをご紹介していきました。
テストセンターでSPIを受検する場合は推論で点数を取れるかが非常に重要です。総当たり戦の問題が出題されたときは必ず対戦表を書く癖を付けましょう。


