SPIの非言語では大学生350人問題が出題されることがあります。
※「SPIとは？対策方法や問題・例題をすべて紹介！適性検査SPIはこれで完璧だ！」もぜひ合わせてご覧ください。
大学生350人問題は集合に関する問題で、難易度は少し高めです。
SPIで高得点を狙っている人は必ず対策しておきましょう。
今回はSPIの受検回数＝100回超・日本トップレベルにSPIを熟知しているSPIマスターの私カズマが、SPIで出題される大学生350人問題の解き方やポイントについて例題を使いながら解説します。
SPIを受検予定の就活生や転職活動中の社会人はぜひ最後までご覧ください。
ちなみにですが、SPIにはたった3時間の勉強でSPIが通過してしまう勉強法があります。
これさえあれば限りなく少ない努力で内定に大きく近づきます。
これは私が100回以上ものSPI受検を通して生み出した、どの本にも載っていない超コスパの良い究極の勉強法です。
興味のある人はぜひ以下のボタンからその方法をチェックしてみてください。
SPIの大学生350人問題とは？例題をご紹介
SPIの非言語（数学）で出題される大学生350人問題は以下のような問題です。
※SPIの非言語（数学）を完全解説した記事もぜひ参考にしてください。
制限時間＝1分30秒を目安に解いてみてください。
【例題】
大学生350人に授業AとBの履修状況を尋ねた。授業Aの履修者と授業A、Bのどちらも履修していない人の比率が3：1で、授業A、Bをともに履修している人は授業Bのみを履修している人の半数だった。授業A、Bの少なくとも一方は履修している人が287人のとき、授業Aのみを履修している人は何人か求めよ。
【解答＆解説】
「授業A、Bをともに履修している人は授業Bのみを履修している人の半数だった」に注目します。
授業Bのみを履修している人の数を2b[人]とすると、授業A、Bをともに履修している人の数はb人となります。
また、授業Aのみを履修している人の数をa人とします。
すると、以下のようなベン図を描くことができます。
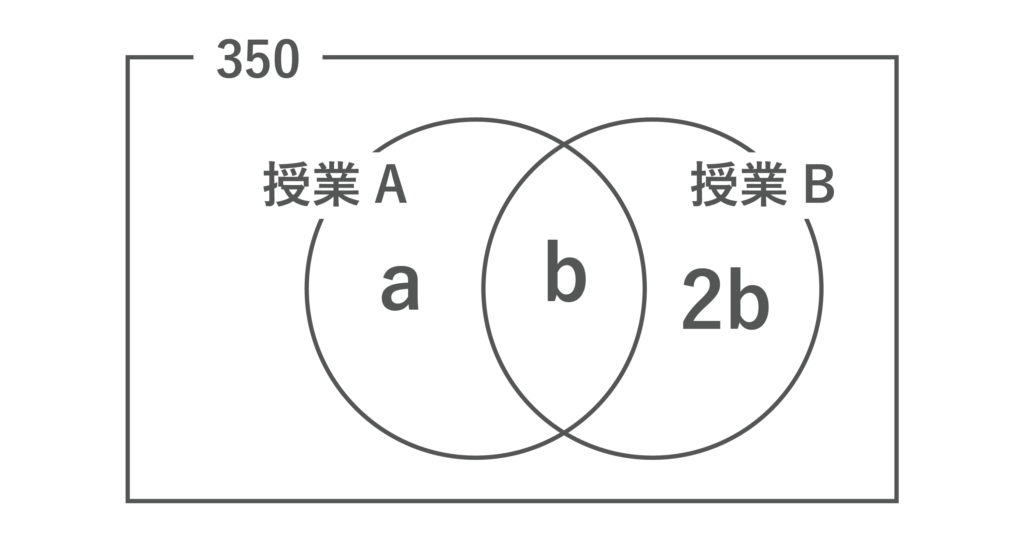
すると「授業Aの履修者と授業A、Bのどちらも履修していない人の比率が3：1」という条件から、
（a＋b）：（350-a-3b）＝3：1
という式を立てることができます。
内項の積＝外項の積より、1050-3a-9b＝a＋bとなり、整理すると4a＋10b＝1050・・・（1）となります。
※内項の積＝外項の積がわからない人は「SPIの割合と比の解き方とコツ！暗記必須の公式とは？練習問題付き」をご覧ください。
また、「授業A、Bの少なくとも一方は履修している人が287人」という条件から、
a＋b＋2b＝287という式を立てることができます。これを整理すると、a＋3b＝287・・・（2）となります。
（1）と（2）を連立方程式として解いていきます。
（2）×4-（1）より、2b＝98となります。つまり、b＝49です。
これを（2）に代入すると、a＋3×49＝287より、a＝287-147＝140[人]・・・（答）となります。
※連立方程式の解き方がわからない人は「【SPI】方程式はこの2つだけ絶対覚えよう！例題でわかりやすく解説！練習問題付き」をご覧ください。
【SPI】大学生350人問題のポイント
以上で大学生350人問題の例題をご紹介しましたが、ポイントは授業Bのみを履修している人の数を2b[人]とおくことです。
すると、授業A、Bをともに履修している人の数は2b÷2＝b[人]と自然に導くことができます。
あとは授業Aのみを履修している人の数をa人として連立方程式を作り、それを解いていくだけです。
集合問題では何を文字におくかが非常に重要ですが、迷ったときはテキトーな箇所を一旦文字にしてみてください。
すると、そこから芋づる式に他の箇所も文字で表せるようになったりします。
また、ベン図を使って集合の問題を解くのが苦手な人はカルノー表を使うのも1つの手段です。
例えば上記でご紹介した大学生350人問題をカルノー表で解いてみると以下のようになります。
※カルノー表の詳細は「SPIのカルノー表とは？具体例で使い方を解説！3つある場合は？」をご覧ください。
【別解】
授業A、Bをともに履修している人の数をb人、授業Aのみを履修している人の数をa人とおきます。
すると、以下のようなカルノー表を作ることができます。
※「〇」＝履修している、「×」＝履修していないを表すものとします。
| 単位：[人] | 授業A：〇 | 授業A：× | 合計 |
|---|---|---|---|
| 授業B：〇 | b | 2b | 3b |
| 授業B：× | a | 350-a-3b | 350-3b |
| 合計 | a＋b | 350-a-b | 350 |
授業Aの履修者と授業A、Bのどちらも履修していない人の比率は3：1なので、上記のカルノー表から
（a＋b）：（350-a-3b）＝3：1・・・（X）
という式を作ることができます。
また、授業A、Bの少なくとも一方は履修している人が287人なので、上記のカルノー表から
b＋2b＋a＝287・・・（Y）
という式を作ることができます。
ここからは上記でご紹介した解答＆解説と同じです。（X）と（Y）の連立方程式を解けばa＝140、b＝49が求まります。
ただし、カルノー表は集合が3つ以上登場すると使えなくなるのでご注意ください。
SPIの非言語（数学）では3つ以上の集合が登場する可能性もあるので、基本的にはベン図を使えるようにしておくのがおすすめです。
SPIの集合については「SPIの集合・ベン図の解き方を例題でわかりやすく解説！コツと練習問題も」でもっと詳しく解説しているので、ぜひ合わせてご覧ください。
練習問題
最後に、SPIの集合に関する練習問題をご用意しました。
※SPIの練習問題433問をすべて無料で掲載している記事もぜひ参考にしてください。
ぜひベン図を使いながら解いてみてください。
【練習問題1】
社会人の習い事について調査したところ、英会話を習っている人は51%、料理を習っている人は35%いた。またどちらも習っていない人は両方とも習っている人の1.5倍だった。このとき、英会話を習っているが料理は習っていない人は回答者全体の何%か求めよ。
【解答＆解説】
英会話51%から両方習っている人を引くと、英会話だけ習っている人が求まります。
まず、両方習っている人を求めます。両方習っている人をx%として、方程式を作っていきます。
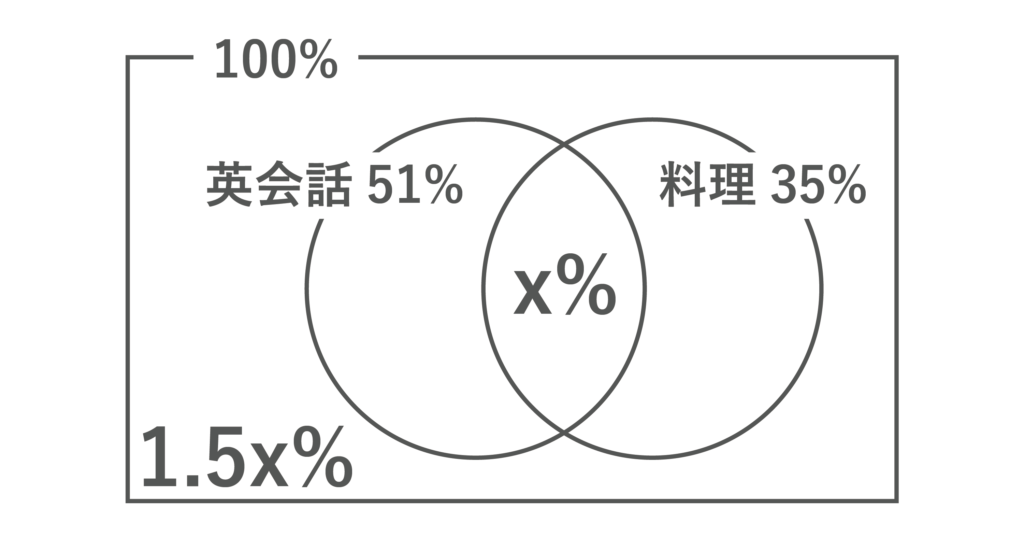
51＋35-x＋1.5x＝100より、0.5x＝14となるので、x＝28[%]となります。
よって、答えは51-28＝23[%]・・・（答）となります。
【練習問題2】
ある公園には城と庭園がある。公園に来た人のうち、城に行った人は89人、庭園に行った人は63人だった。城だけに行った人数が庭園だけに行った人数の2倍だったとき、白と庭園の両方に行った人は何人だったか求めよ。
【解答＆解説】
庭園の63人から、庭園だけに行った人を引くと城と庭園の両方に行った人となります。
まずは庭園だけに行った人を求めます。
庭園だけに行った人をx人として方程式を作りましょう。
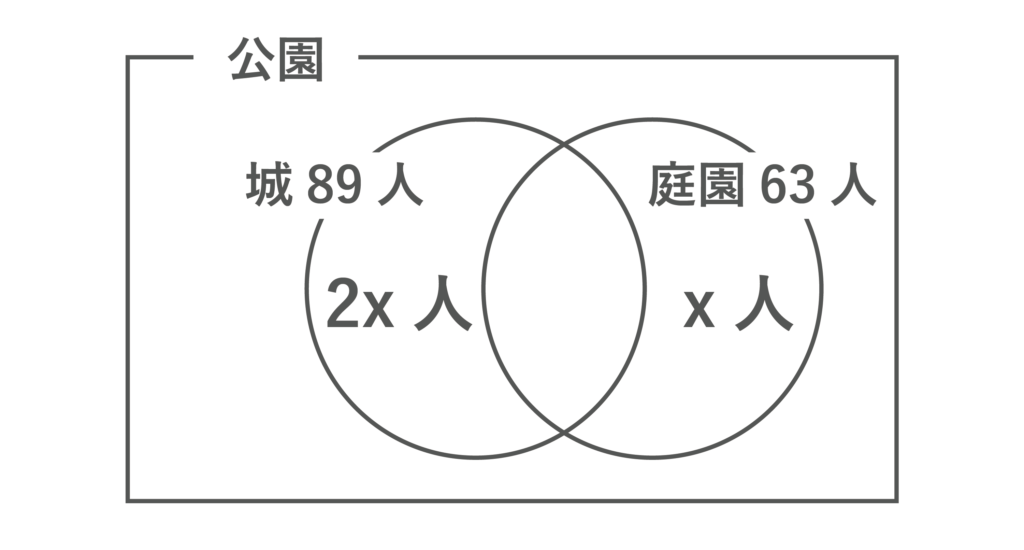
89-2x＝63-xより、-x＝-26となるので、x＝26[人]となります。
よって、答えは63-26＝37[人]・・・（答）です。
🔽 本にも載ってない極秘情報 🔽
今回はSPIの大学生350人問題について解説していきました。
集合問題は苦手な人が多いので、SPIを受検予定の就活生や転職活動中の社会人は必ず勉強・対策しておきましょう。
