
SPIの能力検査では非言語という科目が用意されています。非言語=数学と考えていただいて問題ありません。
※SPIの非言語(数学)を完全解説した記事もぜひ参考にしてください。
そして、公務員試験の教養科目には数的処理という科目が用意されています。数的処理では数学的な思考力・推理力が問われる問題が出題されるため、SPIの非言語と範囲が被るところもあります。
本記事ではSPIの非言語と公務員試験の数的処理の問題を徹底比較してみました。
また、できない人が多いのはどっちかについても解説しています。
SPIや公務員試験を受検予定の就活生や転職活動中の社会人はぜひ参考にしてください。
ちなみにですが、SPIにはたった3時間の勉強でSPIが通過してしまう勉強法があります。
これさえあれば限りなく少ない努力で内定に大きく近づきます。
これは私が100回以上ものSPI受検を通して生み出した、どの本にも載っていない超コスパの良い究極の勉強法です。
興味のある人はぜひ以下のボタンからその方法をチェックしてみてください。
SPIと数的処理の問題を徹底比較
公務員試験の数的処理では判断推理・数的推理・資料解釈・空間把握の4分野から問題が出題されます。
本記事では以上の4分野で出題される問題とSPIの非言語で出題される問題を比較していきます。
判断推理
判断推理は問題文にある複数の条件を整理し、ある事柄を推理・推測する問題です。
【数的処理の判断推理問題1】
※出典:2016年 国家一般職
A〜Eの5人が旅行のため、午前9時00分に駅の改札口前で待ち合わせることになった。次のことがわかっているとき、確実にいえるのはどれか。
ただし、各人の時計は、正確な時刻からずれている可能性があるが、そのずれは一定であるものとする。
ア:Bの時計は、Cの時計よりも2分遅れていたが、Eの時計よりも3分進んでいた。
イ:Eの時計は、Aの時計よりも7分遅れていたが、Dの時計よりも1分進んでいた。
ウ:Aは、自分の時計で午前9時10分に到着し、それはBの到着の5分後であった。
エ:Cは、自分の時計で午前9時05分に到着した。
オ:Eは、自分の時計で午前8時50分に到着し、それはDの到着の15分前であった。
- Aは、2番目に到着した。
- Bは、自分の時計で午前9時03分に到着した。
- Cは、4番目に到着した。
- Dは、自分の時計で午前9時05分に到着した。
- 自分の時計で午前9時00分より前に到着したのは、1人のみであった。
【解答&解説】
各人が到着したときの、ぞれぞれの時計の時刻を表に整理してみます。
まず、ウより、Aが到着したとき、Aの時計は9:10で、Bが到着したのはその5分前なので、Aの時計で9:05とわかります。
同様に、オより、Eが到着したとき、Eの時計は8:50で、Dが到着したのはその15分後なので、Eの時計で9:05とわかります。
| 表1 | Aの時計 | Bの時計 | Cの時計 | Dの時計 | Eの時計 |
|---|---|---|---|---|---|
| Aが到着 | 9:10 | ||||
| Bが到着 | 9:05 | ||||
| Cが到着 | 9:05 | ||||
| Dが到着 | 9:05 | ||||
| Eが到着 | 8:50 |
ここで、イより、Eの時計はAの時計よりも7分遅れているので、D・Eが到着したときのAの時計はEの時計よりも7分先の時刻で、それぞれ9:12と8:57とわかります。
また、アより、Eの時計はBの時計よりも3分遅れており、さらに、Bの時計はCの時計より2分遅れているので、Eの時計はCの時計より5分遅れていることになります。
以上より、Cが到着したときのEの時計は9:00となり、Aの時計では9:07とわかり、以下の表のように、各人が到着したときのAの時計の時刻がわかります。
| 表2 | Aの時計 | Bの時計 | Cの時計 | Dの時計 | Eの時計 |
|---|---|---|---|---|---|
| Aが到着 | 9:10 | ||||
| Bが到着 | 9:05 | ||||
| Cが到着 | 9:07 | 9:05 | 9:00 | ||
| Dが到着 | 9:12 | 9:05 | |||
| Eが到着 | 8:57 | 8:50 |
これより、到着順はE→B→C→A→Dとなり、この時点で1と3は不適であるとわかります。
ここからは2・4・5を順番に確認していきます。
まず2ですが、Bが到着したとき、Aの時計で9:05なので、Eの時計では8:58となり、アよりBの時計はそれより3分進んでいるので、Bの時計では9:01となります。よって、2は不適となります。
続いて4ですが、Dが到着したとき、Eの時計では9:05で、イよりDの時計はそれより1分遅れているので、Dの時計では9:04となります。よって、4は不適となります。
最後の5ですが、表2と2・4から自分の時計で9:00より前に到着したのはEのみなので、5は正しいことがわかります。
以上より、答えは5・・・(答)となります。
上記の判断推理の問題は、SPIの非言語でいうところの推論に近い問題です。
というわけで、以下ではSPIの推論問題をご紹介します。
【SPIの推論問題】
いちごジャム・みかんジャム・ぶどうジャムを合わせて12個買った。それぞれの個数について、以下のことがわかっている。
【1】3種類とも2個以上買った。
【2】いちごジャムの個数は3種類の中で最も多い。
【3】同じ個数のジャムはない。
(1)以下の推論ア・イ・ウのうち、確実に正しいと言えるものはどれか。すべて選びなさい。
ア:いちごジャムの個数は6個以上である。
イ:いちごジャムの個数が5個なら、最も個数の少ないジャムは3個である。
ウ:いちごジャムの個数が6個なら、最も個数の少ないジャムは2個である。
(2)以下の推論カ・キ・クのうち、確実に正しいと言えるものはどれか。すべて選びなさい。
カ:みかんジャムの個数が4個なら、ぶどうジャムの個数は3個である。
キ:みかんジャムの個数が2個なら、ぶどうジャムの個数は4個である。
ク:みかんジャムとぶどうジャムを合わせた個数がいちごジャムより多いなら、いちごジャムの個数は5個である。
【解答&解説】
(1)ア:いちごジャムを5個とすると、他の2種類のジャムの合計は12-5=7[個]となります。
これを3個+4個に分ければ、【1】〜【3】が成り立ちます。よって、いちごジャムは少なくとも5個以上なので、正しいとは言えません。
イ:上記より、いちごジャムの個数が5個のとき、最も個数の少ないジャムは3個となります。よって、正しいことがわかります。
ウ:いちごジャムを6個とすると、他の2種類のジャムの合計は12-6=6[個]となります。
ジャムの個数は最低2個、また、同じ個数にはできないので、2種類のジャムの分け方は2個+4個となります。
以上より、最も個数の少ないジャムは2個であり、正しいことがわかります。
よって、答えはイとウ・・・(答)になります。
(2)カ:みかんジャムが4個のとき、いちごジャムとぶどうジャムの個数の合計は12-4=8[個]となります。
いちごジャムを6個とすれば、ぶどうジャムは2個となるので、ぶどうジャムは3個とは限りません。よって正しいとは言えません。
キ:みかんジャムが2個のとき、いちごジャムとぶどうジャムの個数の合計は12-2=10[個]となります。
いちごジャムを7個とすれば、ぶどうジャムは3個となるので、ぶどうジャムは4個とは限りません。よって正しいとは言えません。
ク:いちごジャムが6個のとき、みかんジャムとぶどうジャムの個数の合計は12-6=6[個]となります。
したがって、みかんジャム+ぶどうジャムがいちごジャムより多くなるには、いちごジャムが6個より少なくなければなりません。
一方で、アより、いちごジャムの個数は少なくとも5個以上なので、みかんジャム+ぶどうジャムがいちごジャムより多くなるのは、いちごジャムが5個の場合のみとなります。よって、正しいことがわかります。
以上より、答えはク・・・(答)となります。
推論問題に関しては公務員試験の方がSPIよりも条件が多く設定されているケースが大半なので、難易度が上がります。
※「SPIの推論とは?すべてがわかる!時間足りない・苦手な人向けの対策方法も解説」もぜひ参考にしてください。
【数的処理の判断推理問題2】
判断推理では集合に関する問題も出題されます。
※出典:2013年 刑務官
A・B・Cの3つの国家資格の保有状況について次のことがわかっているとき、BとCを持っているがAを持っていない人は何人か求めよ。
ア:Aを持っている人は60人、Bを持っている人は50人いた。
イ:AとBを持っているが、Cを持っていない人は12人いた。
ウ:AとCを持っているが、Bを持っていない人は15人いた。
エ:AもBも持っていない人は10人いたが、そのうちCを持っている人は2人いた。
オ:A、B、Cのいずれも持っていない人と、A、B、Cのすべてを持っている人は同じ数だった。
カ:Aのみを持っている人と、Bのみを持っている人の数は同じ数だった。
【解答&解説】
以下のようなベン図を書き、a〜hを設定します(求めるのはfの人数です)
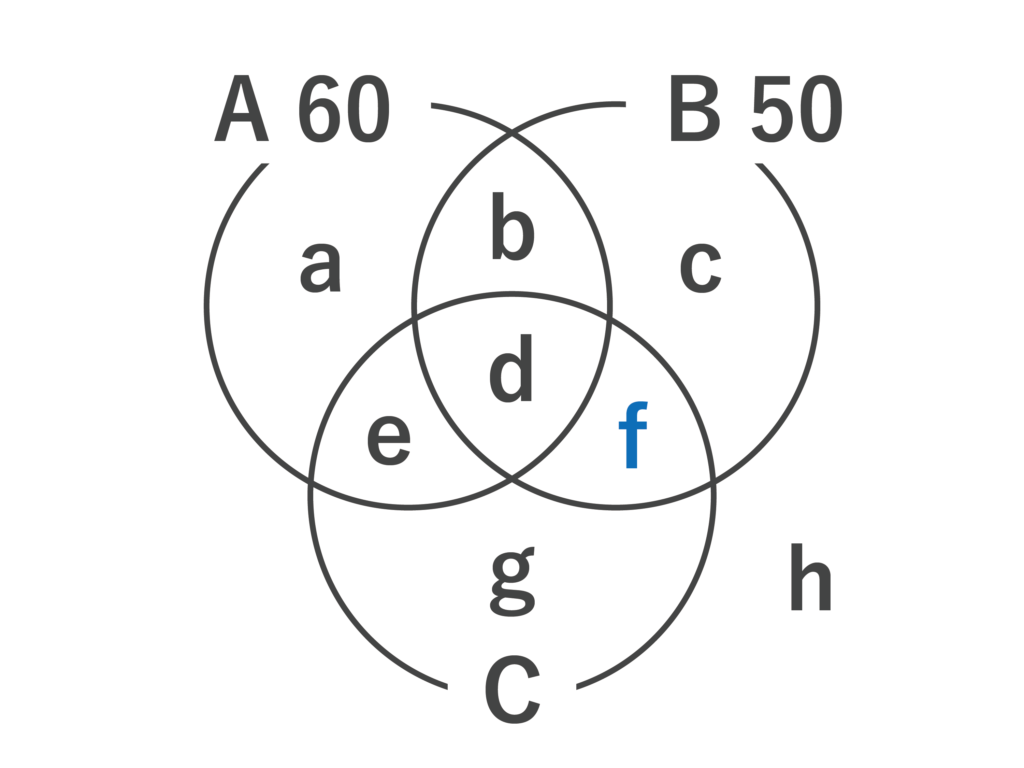
イとウより、b=12、e=15が確定します。
また、エよりg+h=10で、g=2なのでh=8が確定します。
また、オよりd=h=8で、これより、Aについてa=60-(12+8+15)=25となります。
よって、カよりc=a=25がわかります。
以上より、Bについて、f=50-(12+25+8)=5[人]・・・(答)となります。
【SPIの集合問題】
150人の生徒に数学と英語の試験を行った。数学の合格者は85人、英語の合格者は102人、2科目とも不合格であった人は14人であった。2科目とも合格したのは何人いるか求めよ。
【解答&解説】
以下のようなベン図を描いてみます。aは数学合格者、bは両方の合格者、cは英語合格者となります。
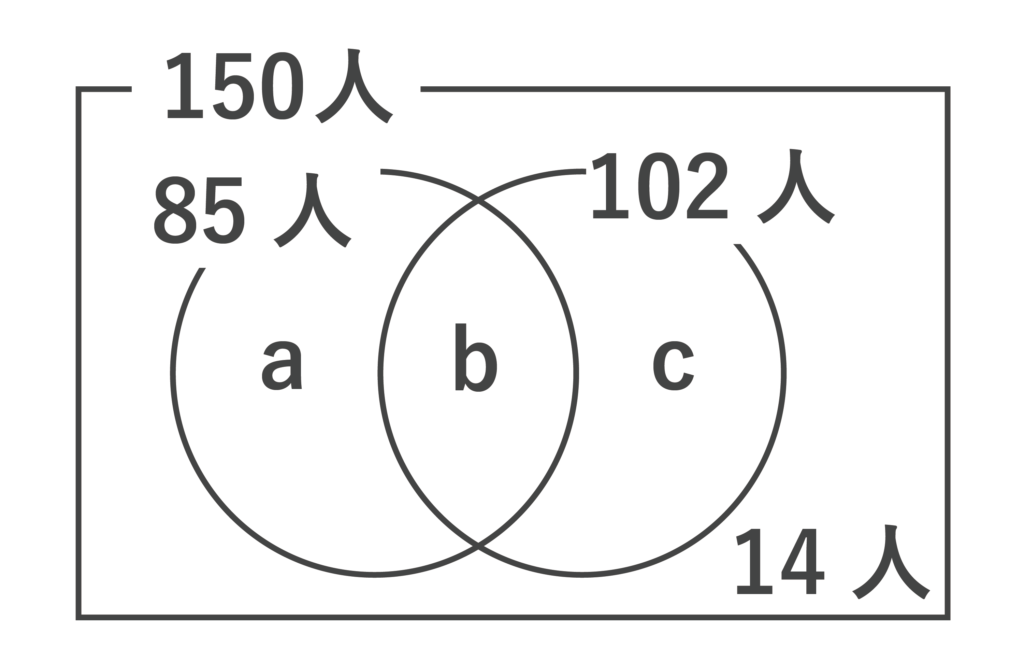
すると、150-(85+102-b)=14という方程式が立てられるので、b=51[人]・・・(答)となります。
集合問題も公務員試験の方がSPIよりも難しいですね。
※「【SPI】集合・ベン図の練習問題13選!解き方や3つ・少なくとものケースまで網羅」もぜひ参考にしてください。
【数的処理の判断推理問題3】
数的処理の判断推理では暗号問題も出題されます。SPIでも暗号問題が出題されるという噂がありますが、それは間違いなのでご注意ください。
※詳しくは「SPIで暗号問題は出ません!CABでは出るので要注意!例題とコツもご紹介」をご覧ください。
※出典:2016年 特別区経験者採用
ある暗号で「TEST」が「31043031」、「FIGHT」が「0512101131」と表されるとき、同じ暗号の法則で「200023」と表されるのは以下のうちどれか。
- BOX
- CAP
- HAT
- MAP
- HIT
【解答&解説】
「TEST」の4文字に対して数字が8桁、「FIGHT」の5文字に対して数字が10桁なので、アルファベット1文字と数字2桁を対応させてみます。
- T=31
- E=04
- S=30
- T=31
また、
- F=05
- I=12
- G=10
- H=11
- T=31
となります。ここで、暗号に使われている数字を見ると、十の位は0〜3、一の位は0〜5なので、一旦これらの数字で以下の表を作成し、対応する文字を記入してみます。
| 0 | 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|---|
| 0 | E | F | ||||
| 1 | G | H | I | |||
| 2 | ||||||
| 3 | S | T |
すると、表に並んだアルファベットの規則性から、空欄は以下のように推測できます。
| 0 | 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|---|
| 0 | A | B | C | D | E | F |
| 1 | G | H | I | J | K | L |
| 2 | M | N | O | P | Q | R |
| 3 | S | T | U | V | W | X |
以上より、20=M、00=A、23=Pとなるので、答えは「MAP」の4・・・(答)となります。
【数的処理の判断推理問題4】
数的処理の判断推理ではサイコロ問題も出題されます。
※出典:2016年 東京都キャリア活用
以下の図のように、同じサイコロ3個を、互いに接する面の目の和がそれぞれ6になるように並べたとき、A、Bの各面の目の数の合計として、正しいのはア〜オのうちどれか。ただし、サイコロの任意の面とその反対側の面の目の数の和は7である。
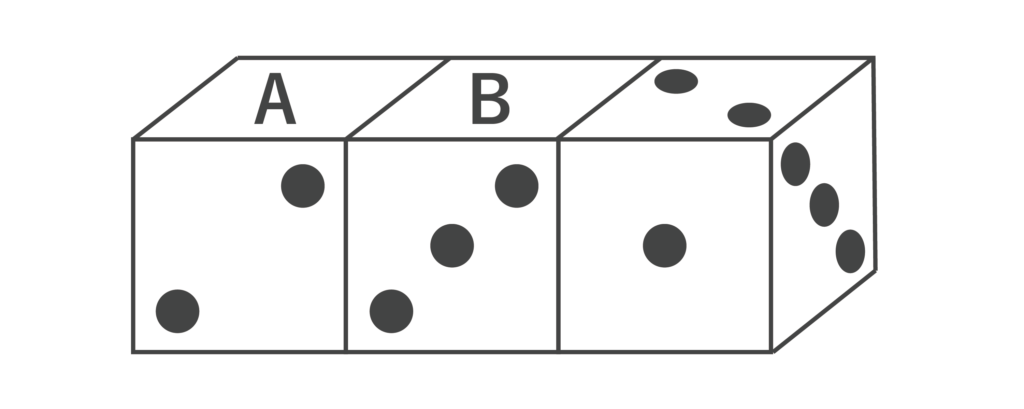
- ア:4
- イ:5
- ウ:6
- エ:7
- オ:8
【解答&解説】
与えられたサイコロをX・Y・Zとし、その目を位相図に表します。反対側の面との目の和が7になるように記入すると、以下の図のようになります。
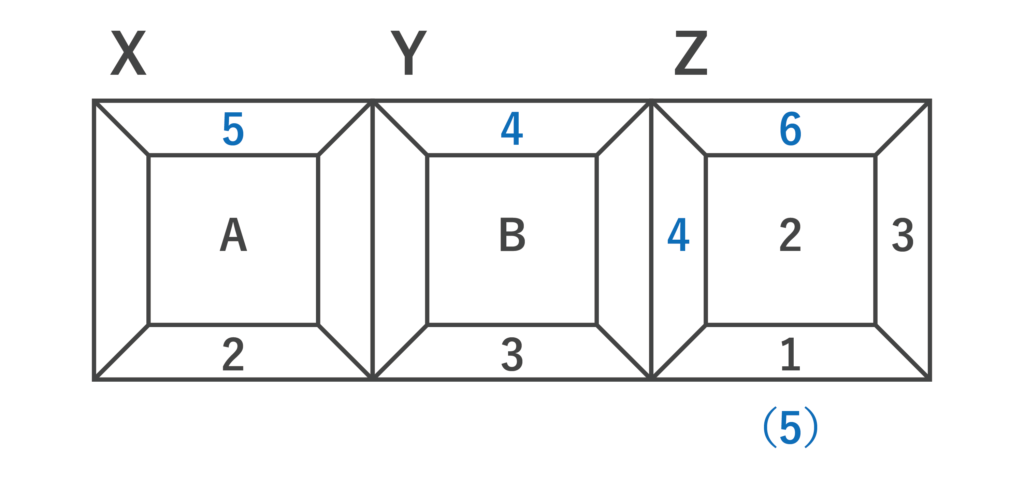
また、互いに接する面の目の和は6なので、Zの4と接するYの面は2、その反対側の面は5で、これと接するXの面は1となり、以下の図のようになります。
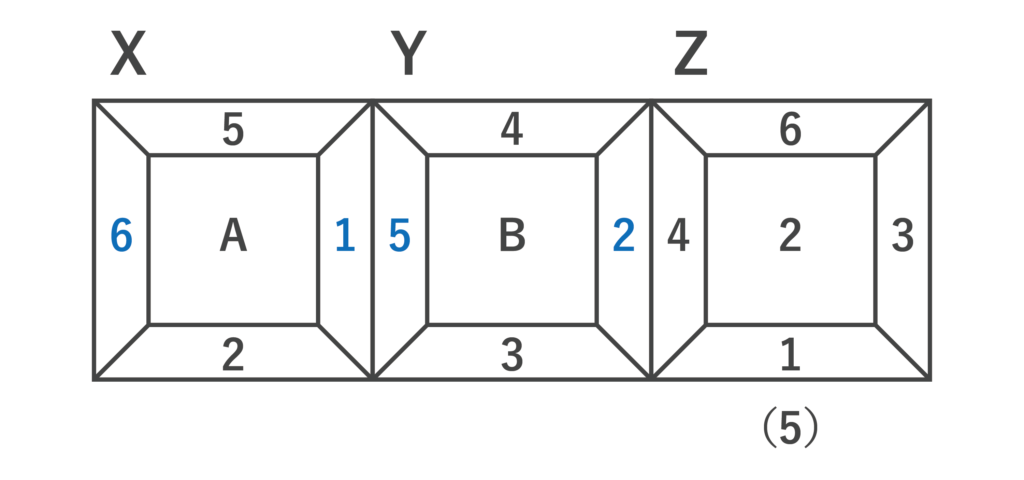
ここで、Xのサイコロについて、1つの頂点を囲む3面の目の配置について調べると、以下の図のように時計回りに1→2→Aと並ぶのがわかります。
以上より、Zのサイコロで、1つの頂点を囲んで1→2→?の並びを調べると、時計回りだと1→2→3、反時計回りだと1→2→4と並ぶのがわかり、Aと一致するのは3とわかります。
同様に、Yのサイコロについても、B→2→3と時計回りに並ぶことから、B=1が確定します。
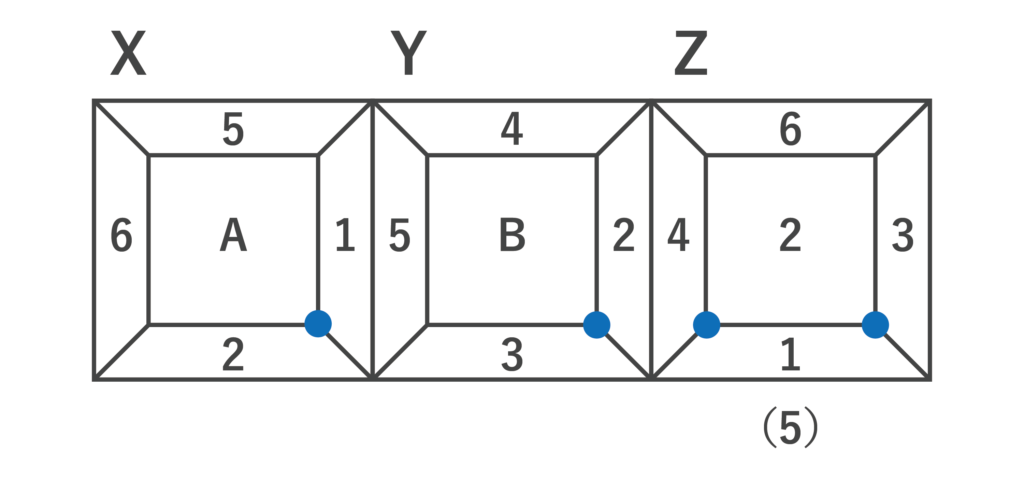
よって、AとBの目の和=3+1=4となるので、答えはア・・・(答)となります。
かなり難易度が高い問題だったのではないでしょうか。
SPIのサイコロ問題は難易度はかなり下がります。
【SPIのサイコロ問題】
2つのサイコロを同時に投げるとき、出た目の積が3の倍数になる確率を求めよ。
【解答&解説】
出た目の積が3の倍数になるのは、2つのサイコロのどちらか一方の出た目が3または6のときです。
逆に言うと、2つのサイコロの出た目が両方とも3と6以外の場合は3の倍数にはなりません。
その確率は4/6 × 4/6=4/9です。よって、出た目の積が3の倍数になる確率は1 – 4/9 =5/9・・・(答)となります。
※「SPIのサイコロ問題の解き方!必見のコツもご紹介します!練習問題も」という記事もぜひ合わせてご覧ください。
🔽 本にも載ってない極秘情報 🔽
数的推理
数的推理では以下でご紹介するような、ごく一般的な数学の問題が出題されます。
【数的処理の数的推理問題1】
※出典:2012年 国家一般職
週末の2日間で行われたイベントで生じた各日のゴミの量について調べたところ、2日目のゴミの量は1日目の1.2倍で、燃えるゴミと燃えないゴミの比は、1日目が13:15、2日目は9:7であった。1日目の燃えないゴミの量を100とした場合、2日目の燃えないゴミの量はいくらか。
【解答&解説】
1日目のゴミの量は、燃えるゴミ:燃えないゴミ:合計=13:15:28なので、1日目の合計の量は燃えないゴミの量の28/15 倍であることがわかります。
また、2日目のゴミの量は1日目の1.2倍=6/5 倍で、燃えるゴミ:燃えないゴミ:合計=9:7:16なので、燃えないゴミの量は全体の量の7/16 倍となります。
以上より、2日目の燃えないゴミの量は、1日目の燃えないゴミの量の28/15 × 6/5 × 7/16 倍となるので、1日目の燃えないゴミの量を100とすると、2日目の燃えないゴミの量は
100 × 28/15 × 6/5 × 7/16 =98・・・(答)となります。
【SPIの割合と比の問題】
A大学のサークルには150人の会員がおり、そのうちの20%が新入生である。新入生以外の会員のうち、40%が男性であるとき、新入生以外の女性は何人か求めよ。
【解答&解説】
新入生の会員数=150×20%=150×0.2=30[人]です。
よって、新入生以外の会員数=150-30=120[人]であることがわかります。
このうちの40%が男性なので、60%が女性ということになります。
よって、答えは120×60%=120×0.6=72[人]・・・(答)となります。
※「【SPI】割合と比の練習問題20問!難しい?公式や解き方・コツもわかりやすく解説!」もぜひ参考にしてください。
【数的処理の数的推理問題2】
※出典:2003年 特別区経験者採用
自転車Aは、線路に平行する道路を午前10時にX駅からY駅に向かって出発した。列車Bは、午前10時30分にY駅を出発し、途中、自転車Aとすれ違ってから1時間後にX駅に到着した。自転車Aは、列車Bとすれ違ってから1時間30分後にY駅に着いたとすると、自転車Aと列車がすれ違った時刻は何時何分か。ただし、自転車Aと列車Bの速度は、どちらも一定とする。
【解答&解説】
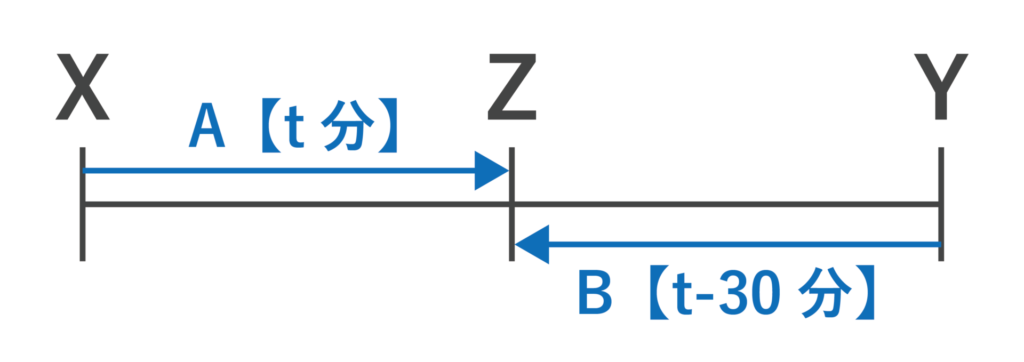
Aが出発してBとすれ違うまでの時間をt分、AとBがすれ違った地点をZとおきます。
すると、AはXZ間を進むのにt分かかったことがわかります。
BはAより30分遅れて出発したので、すれ違うまでにかかった時間はAより30分少ない(t-30)分となります。
以上を図にすると以下のようになります。
また、AとBがすれ違った後、BはZX間に1時間(60分)、AはZY間に1時間30分(90分)かかったことになります。
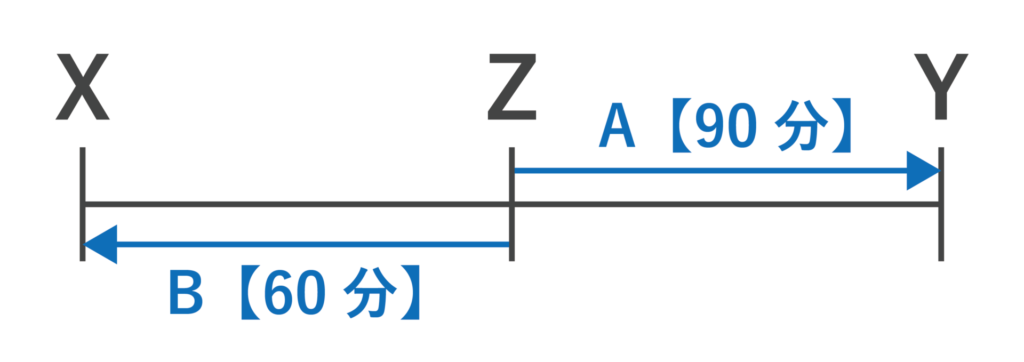
以上より、XZ間とYZ間の距離の比を考えると、Aがそれぞれの距離にかかった時間の比より、XZ:YZ=t:90となります。
また、Bがかかった時間の比よりXZ:YZ=60:(t-30)となります。
よって、t:90=60:(t-30)が成り立ちます。
内項の積=外項の積より、90×60=t(t-30)となるので、
t2-30t-5400=0という二次方程式が立てられます。
これを因数分解すると(t+60)(t-90)=0となるので、t=90となります。
※tは時間を表しているので、t=-60は明らかに不適です。
以上より、答えはAが出発した10時から90分後となるので、11時30分・・・(答)です。
【SPIの速度算の問題】
甲は3km/時で、乙は5km/時で歩くものとする。甲はX地点からY地点まで歩いて40分かかる。甲がX地点からY地点に向かって、乙がY地点からX地点に向かって同時に歩き始めたとき、2人は何分後に出会うか求めよ。
【解答&解説】
甲と乙の速度の和は3+5=8[km/時]です。
X地点とY地点の距離は3 × 40/60=2[km]です。
よって、答えは2 ÷ 8=0.25[時間]=15[分]・・・(答)となります。
※「【SPI】速度算の練習問題18問!コツや解き方・公式・計算方法を完全解説!」もぜひ参考にしてください。
資料解釈
資料解釈は与えられた図や表をもとにして情報を読み取る問題です。
資料解釈は公務員試験の数的処理でもSPIでも出題されますが、もちろん数的処理の方が難易度は高いです。
【数的処理の資料解釈問題】
※出典:2017年 社会人基礎試験
総務部、営業部、製造部からなる会社がある。図は、この会社の2010年と2015年の各部の社員数の推移を示したものである。総務部の社員数が2010年と2015年で同じであったとすると、2010年に対する2015年の社員数について正しいのはどれか。
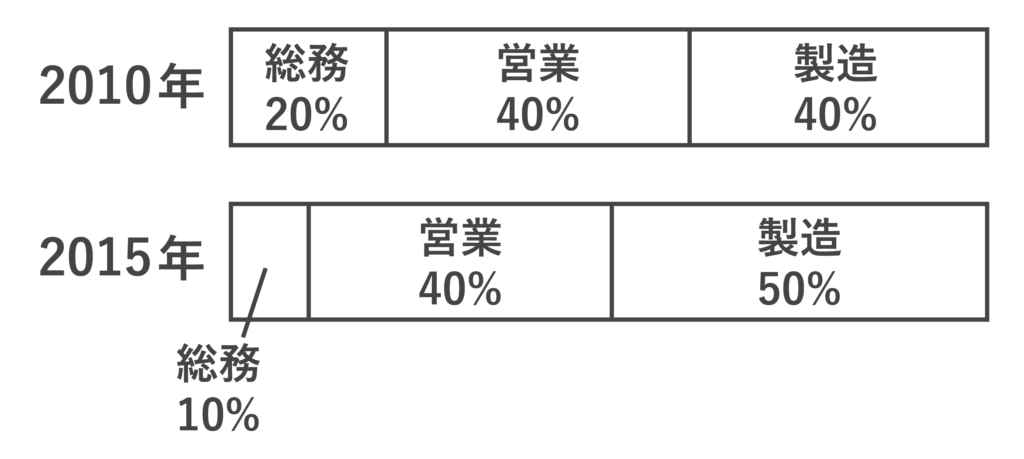
- 会社全体では社員数は減少した。
- 製造部の社員数は1.25倍になった。
- 営業部の社員数は変わらないが、製造部の社員数は増加した。
- 営業部、製造部ともに社員数は増加した。
【解答&解説】
2010年の社員数を100人とおいてみます。
すると、2010年の総務部の社員数は20人ですね。2015年の総務部の社員数は2010年と変わらないので20人です。
10%が20人に相当するので、2015年の会社の社員数は20×10=200[人]であることがわかります。
よって、1は不適であることがわかります。
2に関してですが、製造部の社員数は2010年は100×0.4=40[人]、2015年は200×0.5=100[人]なので、100÷40=2.5[倍]になっています。
よって、2も不適となります。
続いて3ですが、営業部の社員数は2010年は100×0.4=40[人]、2015年は200×0.4=80[人]なので不適です。
最後の4ですが、以上より営業部、製造部ともに社員数は増加していることがわかるので、正しいです。
よって、答えは4・・・(答)となります。
【SPIの資料解釈問題】
A区、B区、C区で選挙を実施し、その選挙結果を集計している。以下の表は政党ごとの得票率である。
| P党 | Q党 | R党 | 無効票 | 投票数 | |
|---|---|---|---|---|---|
| A区 | 45% | 35% | 10% | 10% | 800 |
| B区 | 38% | 50% | 5% | 7% | 600 |
| C区 | 27% | 55% | 8% | 10% | 400 |
(1)B区において、Q党への投票数は何票か求めよ。
(2)C区において、無効票を除いた有効投票数に占めるP党の得票率は何%か求めよ。
【解答&解説】
(1)600×50%=600×0.5=300[票]・・・(答)
(2)C区におけるP党への投票数は400×27%=108[票]ですね。
C区において、無効票を除いた有効投票数=400-400×10%=400-40=360[票]です。
よって、答えは108÷360×100=30[%]・・・(答)となります。
※「SPIの図表の読み取りは対策必須!必ず覚えておくべき知識をご紹介します!練習問題12問付き」もぜひ合わせてご覧ください。
空間把握
空間把握は立体図形や展開図などの空間認識能力を問う問題です。
公務員試験の数的処理で出題され、数的処理の中でも特に難易度が高いのが特徴です。SPIでは出題されません。
本記事では数的処理の空間把握の問題をご紹介します。
【数的処理の空間把握問題】
※出典:2017年 福岡県職務経験者
以下の図のような小正方形16個からなる紙があり、ここから小正方形を1面とする立方体の展開図を切り取る。図の色の付いた3つの小正方形を必ず使うとき、どのような形の展開図を切り取る場合でも、絶対に使うことのない小正方形が2つあるが、それはA〜Gのうちどれか。
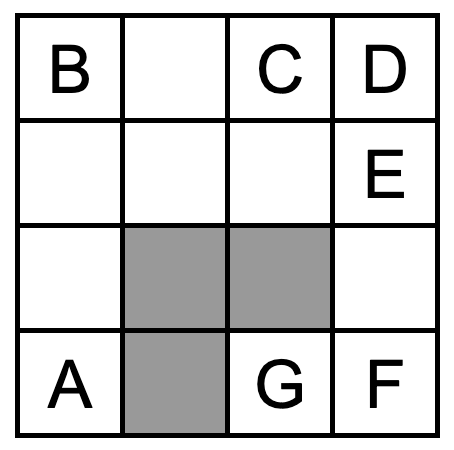
- AとG
- BとF
- CとD
- DとE
- FとG
【解答&解説】
立方体は1つの頂点に3つの面が集まりますが、以下の図1のように、頂点Pの周りに4つの面が集まり、立方体を作ることができません。
また、Fの面を使う場合は、以下の図2のように、Fのすぐ上の面も使うことになりますが、90°をなす辺を重ねると、図のようにアとウの辺がいずれもイの辺と重なってしまうため、立方体を作ることができません。
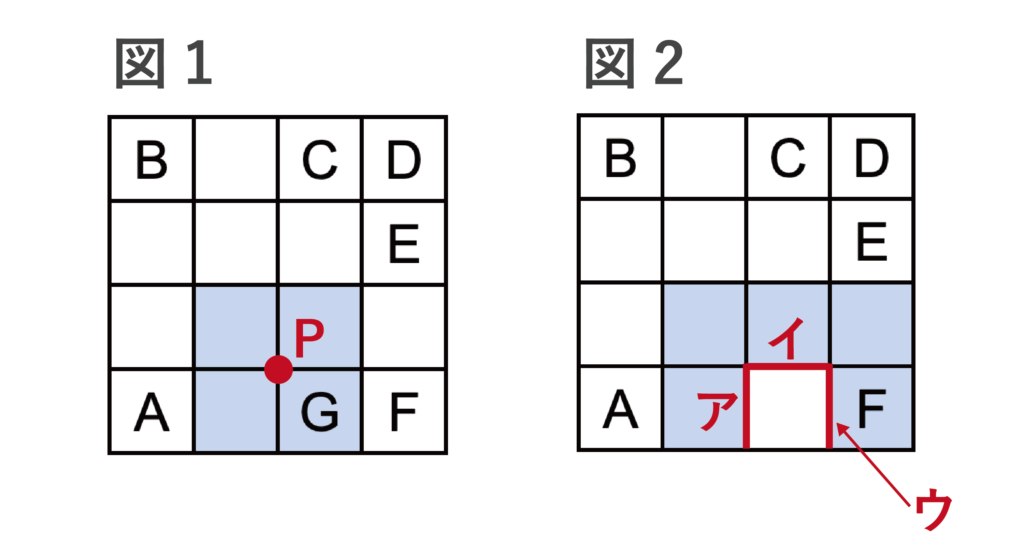
よって、FとGは絶対に使うことがないとわかるので、答えは5・・・(答)となります。
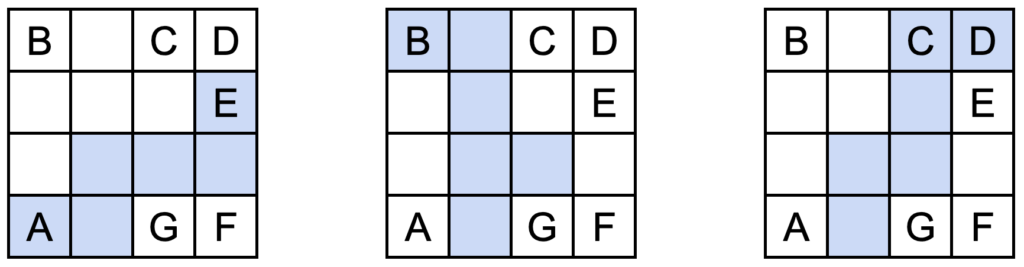
ちなみにですが、A〜Eを含む展開図は、例えば以下の図のように、いずれも可能です。
【SPIと数的処理】できない人が多いのはどっち?
以上でSPIと数的処理の問題をご紹介していきましたが、難易度はご覧いただいた通り数的処理の方が難しいです。
なので、SPIと数的処理を比べた場合、できない人が多いのはもちろん数的処理です。
公務員試験の合格に必要な勉強時間は最低でも800時間といわれており、これは1日4時間の勉強だとおよそ6ヶ月、1日2時間の勉強だとおよそ1年かかる時間です。
それに対して、SPIはSPIを1週間で仕上げる方法について解説した記事でも述べた通り、1週間もあれば十分対策可能なWEBテスト(試験)です。
とは言え、SPIの場合でも0点や壊滅的な点数を取ってしまう人はいるので、ご注意ください。
※「SPIの非言語は0点・ボロボロ・壊滅的でも通過・内定する?受かった事例は?転職は?」もぜひ参考にしてください。
SPI対策の時間が1週間も取れない人は一夜漬けでもなんとかなる可能性もあります。
※詳しくはSPIを一夜漬けでなんとかする方法について解説した記事をご覧ください。
ちなみにですが、SPIにはたった3時間の勉強でSPIが通過してしまう勉強法があります。
これさえあれば限りなく少ない努力で内定に大きく近づきます。
これは私が100回以上ものSPI受検を通して生み出した、どの本にも載っていない超コスパの良い究極の勉強法です。
興味のある人はぜひ以下のボタンからその方法をチェックしてみてください。


