
SPIの非言語(数学・計数)では推論という問題が出題されます。
※「SPIとは?対策方法や問題・例題をすべて紹介!適性検査SPIはこれで完璧だ!」もぜひ合わせてご覧ください。
しかし、推論問題は非言語の中でも最も難しいと言われているため、苦手な人も多いです。
※SPIの推論とは何かについて徹底解説した記事もぜひ参考にしてください。
人によっては、最初から推論問題は捨てて、他の問題で点数を取れるようにSPIの勉強をするのも戦略の1つとしてはありでしょう。
本記事ではSPIに関して日本一詳しいSPIマスターの私カズマが、SPIの推論問題はどんな問題なのか?について例題で解説した後、解き方のコツや難しさ・捨てるべき人とそうでない人などについても解説をしていきます。
※「SPIの非言語(数学)を完全解説!対策方法やできない人でも点数を上げる方法!問題もご紹介」もぜひ合わせてご覧ください。
ちなみにですが、SPIにはたった3時間の勉強でSPIが通過してしまう勉強法があります。
これさえあれば限りなく少ない努力で内定に大きく近づきます。
これは私が100回以上ものSPI受検を通して生み出した、どの本にも載っていない超コスパの良い究極の勉強法です。
興味のある人はぜひ以下のボタンからその方法をチェックしてみてください。
目次
【SPI】推論問題の例題(テストセンター)
SPIにはWEBテスティング、テストセンター、インハウスCBT、ペーパーテストという4つの受検方式がありますが、推論問題はすべての受検方式の出題範囲に含まれています。
SPIを受検予定の就活生や転職活動中の社会人は必ず対策しておきましょう。
※「【SPI】転職・中途採用の対策法や問題・通過率などをSPIマスターが完全解説」もぜひ参考にしてください。
テストセンターとペーパーテスト、WEBテスティングとインハウスCBTはほぼ同じ問題が出題されますが、テストセンターで出題される推論問題とWEBテスティングで出題される推論問題は少し毛色が違うので注意が必要です。
※SPIのペーパーテストを完全解説した記事もぜひ参考にしてください。
まずはテストセンターで出題される推論問題からご紹介していきます。
テストセンターでは以下8つの推論問題が出題範囲となっています。
- 正誤
- 内訳
- 順序
- 整数
- 平均
- 割合
- 対戦
- 位置関係
それぞれ順番に解説していきます。
1:正誤
正誤に関する推論問題では「〜が正しければ、〇〇も必ず正しい」という選択肢が用意されているのが特徴です。
【例題】
花子さんは4人きょうだいのうちの最年少で、女性であることがわかっている。このきょうだいについて、P・Q・Rから以下の発言があった。
- P:花子さんは三女ではない
- Q:花子さんには兄が2人いる
- R:3番目の年長者は次男である
以上の発言は必ずしもすべて正しいとは限らない。そこで、様々な場合を想定して以下の推論がなされた。以下の選択肢1〜3のうち、正しいものを1つ選びなさい。
- Pが正しければQは必ず正しい
- Qが正しければRは必ず正しい
- Rが正しければPは必ず正しい
【解答&解説】
順番に1から見ていきましょう。
Pの「花子さんは三女ではない」が正しいということは花子さんは4人のきょうだいのうちの最年少かつ長女である可能性があります。この場合、花子さんには兄が3人いることになります。
よって1は不適であることがわかります。
続いて2ですが、Qの「花子さんには兄が2人いる」が正しいということは、年長者から順番に「男・男・女・花子さん」である可能性があります。この場合、3番目の年長者は長女なので、2も不適となります。
最後に3ですが、「3番目の年長者は次男である」が正しいということは、年長者もしくは2番目の年長者が男であるということです。つまり、花子さんの上には長女が1人いることになります。
よって「花子さんは三女ではない」も正しくなります。したがって、答えは3・・・(答)となります。
2:内訳
内訳は人やモノの数の内訳の数に関する推論問題です。
【例題】
男性3人、女性2人からなるP・Q・R・S・Tの日本人5人がそれぞれ北海道、沖縄、カナダ、イギリス、フランスの5ヶ所に旅行した。
これについて、以下4つのことがわかっている。
- 男性のうち2人は海外に行った
- PとQは国内に行った
- Rはヨーロッパへ行った
- Sは女性でフランスへ行った
このとき、以下1〜3の推論のうち必ず正しいと言えるものをすべて選びなさい。
- Pは男性である
- Rは男性である
- Tはカナダへ行った
【解答&解説】
与えられた4つの条件を表にすると以下の要素が確定します。
| P | Q | R | S | T | |
|---|---|---|---|---|---|
| 性別 | 男 | 女 | 男 | ||
| 行き先 | 国内 | 国内 | イギリス | フランス | カナダ |
すると、PとQは(P、Q)=(男、女)(女、男)の2通りがあるので1は不適となります。
2の「Rは男性である」は正しいことがわかります。
3の「Tはカナダへ行った」も正しいことがわかります。よって答えは2と3・・・(答)です。
🔽 本にも載ってない極秘情報 🔽
3:順序
順序はその名の通り順番や並び方を問う推論問題です。
【例題】
A・B・C・D・Eの5チームでレースを行い、以下3つのことがわかっているとき、1位からの順位を左から順に表したものはどれか。選択肢1〜5の中から1つ選びなさい。ただし、同着はないものとする。
- BはEよりも早くゴールしたが、1位ではない
- EのタイムはBとCのタイムの平均と等しい
- Aは3位である
- BCADE
- DBAEC
- ECABD
- CBADE
- BDAEC
【解答&解説】
「BはEよりも早くゴールしたが、1位ではない」ことと「EのタイムはBとCのタイムの平均と等しい」ことから「BEC」という並びは確定になります。
そして、残るはAとDですが、Aは3位なので「DBAEC」とすれば辻褄が合います。
よって答えは2・・・(答)となります。
4:整数
整数に関する推論問題は頻出なので、推論の中でも特に重点的に勉強・対策しておきましょう。
※「SPIの対策方法・勉強法を日本一SPIに詳しい筆者が真剣に考えてみた」もぜひ合わせてご覧ください。
【例題】
各階に2戸ずつ、合計で6戸ある3階建てのアパートの各戸にA・B・C・D・E・Fの6世帯が1世帯ずつ住んでいる。以下P〜Sのことがわかっているとき、2階には何人の人が住んでいるか。選択肢1〜8より当てはまるものをすべて選びなさい。
- P:単身世帯はない
- Q:6世帯の合計人数は17人である
- R:B、C、Eはいずれも3人世帯である
- S:BとCは1階に住んでいる
- 3人
- 4人
- 5人
- 6人
- 7人
- 8人
- 9人
- 10人
【解答&解説】
SPIでは世帯に関する問題が時々出題されるので慣れておきましょう。
「【SPI】平均世帯人数とは?求め方・計算方法を例題でわかりやすく解説」もぜひ合わせてご覧ください。
各階の人数は、
- 1階=RとSより3人世帯×2=6人
- 2階=Pより、単身世帯はないので最小で2×2=4人
- 3階=2世帯なので最小で4人
よって、2階と3階は最多で17-6-4=7[人]となります。
したがって、2階には4〜7[人]が住んでいることがわかるので答えは2、3、4、5・・・(答)となります。
5:平均
その名の通り平均に関する推論問題です。
【例題】
50個のお菓子をP・Q・R・S・Tの5人に配った。配られたお菓子の個数について以下のことがわかっている。
- 同じ個数の人はいない
- P・Q・Rの平均は12個である
- PとRでは11個の差がある
- QとS、QとTはそれぞれ3個の差がある
このとき、10個配られた人は誰か。当てはまるものを以下の選択肢1〜5の中からすべて選びなさい。
- P
- Q
- R
- S
- T
【解答&解説】
P・Q・Rの平均は12個であることから、P+Q+R=12×3=36[個]であることがわかります。
ここで、P+Q+R+S+T=50[個]なので、S+T=50-36=14[個]であることがわかります。
そして、QとS、QとTはそれぞれ3個の差があることから、SとTは6個差または同じ個数であることがわかりますが、「同じ個数の人はいない」とのことなので、SとTは6個差であることがわかります。
S+T=14より、(S、T)=(4、10)または(10、4)です。
よって答えは4と5・・・(答)になります。
6:割合
割合(増加率や%など)に関する推論問題となります。推論の中でも難易度は低いので、出題されたらぜひ得点に繋げたい問題です。
【例題】
あるコンビニの売上は前年比で毎年10%ずつ増加している。このとき、以下の推論について正しいものを1〜3の中から1つ選びなさい。
推論:このコンビニの売上は、この3年間で当初よりも30%増加した
- 正しい
- 誤り
- どちらとも言えない
【解答&解説】
SPIの非言語では増加率の計算が頻出なので、必ずできるようにしておきましょう。
※詳しくはSPIの増加率について解説した記事をご覧ください。
当初の売上を100とすると、
- 1年後=100×1.1=110
- 2年後=110×1.1=121
- 3年後=121×1.1=133.1
となるので、およそ33%増加していることがわかります。よって答えは2の誤り・・・(答)となります。
7:対戦
対戦成績や総当たり戦に関する推論問題が出題されます。
※SPIの総当たり戦を解くコツについて解説した記事もぜひ合わせてご覧ください。
【例題】
P・Q・R・S・T・U・V・Wの8人がトーナメント形式で戦った。以下2つのことがわかっているとき、Wが1回戦で対戦したのは誰か。当てはまるものを選択肢1〜7の中からすべて選びなさい。
- Pは順不同でS、T、Vと対戦した
- Wは2回戦でR、Tと戦う可能性があった
- P
- Q
- R
- S
- T
- U
- V
【解答&解説】
「Wは2回戦でR、Tと戦う可能性があった」という情報より、RとTは1回戦で戦っていたことがわかります。
また、「Pは順不同でS、T、Vと対戦した」よりPとWは戦っていないことがわかります。
以上のことをトーナメント表にすると、以下のようになります。
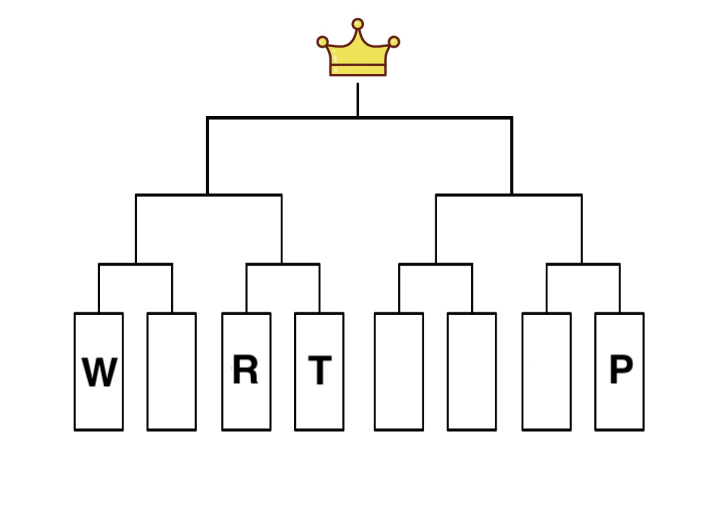
よって、Wと1回戦で戦ったのはQまたはUと考えられるので、答えは2と6・・・(答)になります。
8:位置関係
最後は位置関係に関する推論問題です。座席の配置や方角などが問われます。
※「SPIで方角に関する問題は出る?出ますが推論で出るので要注意!」もぜひ参考にしてください。
【例題】
A〜Eの5人が以下の図のようにカウンターに向かって一列に並んで座っている。各自の座り方について、以下のことがわかっている。
- Aの隣は空席だった
- BとCは隣り合っていた
- 両端(1と6)の席は埋まっていた

DとEが隣り合っていたとき、Aの座った可能性がある場所は上記の図における1〜6のどこか。すべて選びなさい。
【解答&解説】
DとEが隣り合っていたということから、DE(ED)をワンセットで考えます。
同様に、A◯、BCもワンセットで考えます(◯は空席を表すものとする)
すると、1と6は空席ではないので、A◯が端に来るときは必ずAが端となることがわかります(例:A◯BCDE)
A◯が端に来ないときは、A◯、◯Aのどちらもあり得ます(例:BCA◯DE、DE◯ABC)
よってAの席は2と5以外であることがわかるので、答えは1、3、4、6・・・(答)となります。
以上がテストセンターで出題される推論の例題となります。繰り返しにはなりますが、整数の推論問題は頻出なので、特に重点的に勉強しておきましょう。
※SPIのテストセンターとは何かについて詳しく解説した記事もぜひ参考にしてください。
【SPI】推論問題の例題(WEBテスティング)
続いてはWEBテスティングで出題される推論問題をご紹介していきます。
WEBテスティングの推論問題では以下の例題のように「アだけでわかるが〜、イだけでわかるが〜」のような問題が出題されます。
※SPIのWEBテスティングを完全解説した記事もぜひ合わせてご覧ください。
【例題】
以下についてア・イの情報のうち、どれがあれば[問]の答えがわかるかを考え、選択肢1〜5の中から正しいものを1つ選びなさい。
22個のチョコをX、Y、Zの3人で分ける。ただし、全員が少なとも1個はもらうものとする。
[問]Yはチョコを何個もらったか。
【ア】XはYより6個多くもらった
【イ】YはZの半分の個数だった
- アだけでわかるが、イだけではわからない
- イだけでわかるが、アだけではわからない
- アとイの両方でわかるが、片方だけではわからない
- アだけでも、イだけでもわかる
- アとイの両方があってもわからない
【解答&解説】
アよりX=Y+6・・・①、イよりY=Z/2・・・②という式を立てることができますね。
また、X+Y+Z=22・・・③です。
①を③に代入すると、2Y+Z=16となるので、Y=8-Z/2となることがわかります。
Yは自然数なので、(Y、Z)=(2、7)(4、6)・・・と複数個のパターンが存在してしまいます。
よって、アだけでは全員の個数は決まらないことがわかります。
続いて、②を③に代入すると、X+3Y=22より、Y=(22-X)/3となることがわかります。
Yは自然数なので、(X、Y)=(1、7)(4、6)・・・とこちらも複数個のパターンが存在してしまいます。
よって、イだけでも全員の個数は決まらないことがわかります。
では、アとイを組み合わせるとどうなるでしょうか?
①と②を③に代入すると、4Y+6=22より、Y=4が確定します。
このとき、X=4+6=10、Z=2×4=8となるので条件を満たしていることがわかります。
よって答えは3の「アとイの両方でわかるが、片方だけではわからない」となります。
🔽 本にも載ってない極秘情報 🔽
SPIの推論問題のコツ4つ
SPIの推論問題を解くコツとしては以下の4つがあげられます。
- 問題文を丁寧に読み込む
- 徹底してメモを取る
- 表が書けそうなものは表にしてみる
- 方程式を解く練習をしておく
それぞれ順番に解説していきます。
1:問題文を丁寧に読み込む
SPIでは問題1問1問に対して制限時間が設定されており、制限時間を過ぎると自動的に次の問題に移ってしまいます。
制限時間の目安としては1問1分ですが、推論は少し難易度が高いこともあり、1問2分くらいに設定されているケースが多いです。
推論問題は問題文にヒントが隠されていることがほとんどなので、慌てずにしっかりと問題文を丁寧に読み込む癖をつけましょう。
2:徹底してメモを取る
問題文に記載されている情報をしっかりと読み込んだら、その情報を整理することが重要です。
例えば、位置関係に関する推論問題では空欄の場所は「◯」で表現する、AとBをワンセットで考えるときは(AB)と記載するなど、自分なりのルールを決めておきましょう。
3:表が書けそうなものは表にしてみる
情報整理の方法ですが、表が書けそうなものは表にしてみると良いでしょう。
表にすることで視覚的にも情報がわかりやすくなり、問題が解きやすくなります。
表が使える場面が多い推論問題は内訳・対戦・位置関係です。
これら3つの推論問題が出題されたら、表で情報を表現できないか?をぜひ考えてみてください。
4:方程式を解く練習をしておく
これは特にWEBテスティングにおける推論問題を解くコツになりますが、上記で取り上げた例題のように、X+3Y=22からX、Yがともに自然数になる組み合わせを考えたりする場面が頻繁に登場します。
この場合、X+3Y=22をY=(22-X)/3に変形することで、Yが自然数であることから22-Xは3の倍数でなければならないことがわかります。
よって、22-Xは3、6、9、12、15、18、21のいずれかになることがわかります。
このような一次方程式の活用はWEBテスティングの推論問題では頻出なので、必ず対策しておきましょう。
※「【SPI】方程式はこの2つだけ絶対覚えよう!例題でわかりやすく解説!練習問題付き」もぜひ合わせてご覧ください。
SPIの推論問題は難しい?
SPIの推論問題は多くの人が難しいと感じています。
実際に、Twitterでは以下のようなツイートがたくさん見受けられます。
SPIの推論って揚げ足取りみたいでむずい
出典:@ZZjuxIIZgaZXkxa
初めてSPI手付けてみたけど非言語めっちゃむずい!推論がマジ無理(;_;)
出典:@naichel410
また、Yahoo!知恵袋にも以下のような投稿をたくさん見つけることができます。
SPIの推論の問題が難しすぎるんですけど、解くコツとか考え方とかありますか?
出典:Yahoo!知恵袋
SPIの推論系の問題がまじで苦手です。
出典:Yahoo!知恵袋
就職試験で一番でるところなので克服したいのですがどうやったら解けるようになりますか?
SPIの非言語(数学)は非常に幅広い分野から問題が出題されますが、その中でも推論問題は間違いなく難しいと言えるでしょう。
数学の公式がそのまま使えない問題がほとんどであるため、解き方のコツを理解していたり、問題そのものに慣れていないと、初見で解くのはなかなか難しいかもしれません。
※SPIの公式一覧(非言語・数学)をまとめた記事もぜひ参考にしてください。
SPIで高得点を狙っている人は必ず事前に勉強・対策をしておきましょう。
ちなみにですが、テストセンターの非言語では序盤の問題で不正解が多いと推論問題が出ないケースが多いです。推論問題がどれくらい出たか?で自分が高得点かどうかわかります。
詳しくは「SPIで推論出ないのはヤバい?チェックボックスが出たら高得点?」をご覧ください。
SPIの推論問題を捨てるべき人とそうでない人
最後にSPIの推論問題を捨てるべき人とそうでない人の違いについて解説します。
まず、推論問題を捨てるべき人ですが、それは非言語(数学)がかなり苦手な人です。
SPIの非言語は難しいと感じている人も多く、ボロボロ・壊滅的な点数を取ってしまう人もたくさんいます。
※「SPIの非言語は0点・ボロボロ・壊滅的でも通過・内定する?受かった事例は?転職は?」もぜひ参考にしてください。
そのような人は難しい推論問題の対策を行うよりも、速度算や損益算など出題頻度が高い分野の対策を行うようにしてください。
SPIの非言語で対策の優先度が高いのは難易度がそこまで高くないかつ出題頻度が高い分野です。
ちなみにですが、SPIにはたった3時間の勉強でSPIが通過してしまう勉強法があります。
これさえあれば限りなく少ない努力で内定に大きく近づきます。
これは私が100回以上ものSPI受検を通して生み出した、どの本にも載っていない超コスパの良い究極の勉強法です。
興味のある人はぜひ以下のボタンからその方法をチェックしてみてください。
一方で、SPIの推論問題を捨てるべきではない人はSPIで高得点を狙っている人です。
特にテストセンターの非言語では推論問題がたくさん出題されたり、推論問題のチェックボックス問題が出題されたら高得点である可能性が高いです。
※SPIのチェックボックスとは何かについて詳しく解説した記事もぜひ合わせてご覧ください。
テストセンターで高得点を取るためには推論問題は欠かせません。
WEBテスティングの推論問題ではチェックボックス問題は出題されませんが、テストセンターと同じく高得点を目指すのであれば推論問題の対策は必須です。
※SPIの高得点目安・指標について詳しく解説した記事もぜひ参考にしてください。
今回はSPIの推論問題の例題やコツ、難易度・捨てるべき人とそうでない人の違いについて解説していきました。
推論問題は初見で解くのはなかなか難しいので、SPIを受検予定の人は必ず事前に問題の内容を理解しておくことをおすすめします。


