
テストセンター型のSPIの非言語(数学)では最低限問題という問題が出題される可能性があります。
最低限問題は推論の分野で出題される問題で、難易度が高いので対策は必須です。
今回はSPIの受検回数100回超、日本一SPIを熟知しているSPIマスターの私カズマがSPIの最低限問題とは何かについて例題で解説した後、最低限問題が出題されたら高得点なのか?などについて解説していきます。
SPIを受検予定の就活生や転職活動中の社会人はぜひ参考にしてください。
ちなみにですが、SPIにはたった3時間の勉強でSPIが通過してしまう勉強法があります。
これさえあれば限りなく少ない努力で内定に大きく近づきます。
これは私が100回以上ものSPI受検を通して生み出した、どの本にも載っていない超コスパの良い究極の勉強法です。
興味のある人はぜひ以下のボタンからその方法をチェックしてみてください。
SPIの最低限問題とは?例題で解説
SPIの最低限問題とは非言語(数学)の推論で出題される問題の1つです。
※SPIの非言語(数学)を完全解説した記事もぜひ参考にしてください。
推論は与えられた情報・条件からどんなことが推論(推測)できるかを考える問題です。
そして、最低限問題とは「これらの条件のうち、少なくともどの条件があれば〇〇が分かるか?」という問題のことです。
推論の中では最も難易度が高いと言われています。
説明だけではイメージがつかないと思うので、最低限問題の例題を1問ご紹介します。
【例題】
P・Q・R・Sの4人が待ち合わせをした。4人が待ち合わせ場所に到着した順番について以下3つのことがわかっている。
【1】同時に到着した人はいない
【2】RはQより前に到着した
【3】最後に到着したのはPではない
このとき、各問に答えよ。
(1)以下の推論ア・イ・ウのうち、確実に正しいと言えるものはどれか。該当するものをすべて選びなさい。
ア:PはSよりも先に到着した
イ:最後に到着したのはRではない
ウ:1番最初に到着したのはSではない
(2)最も少ない情報で4人の到着した順番がすべてわかるために、上記【1】〜【3】に加えて必要な情報は以下のカ・キ・クのうちどれか。該当するものをすべて選びなさい。
カ:Pの次にRが到着した
キ:Sの次にQが到着した
ク:Qの次にPが到着した
【解答&解説】
(1)【2】より、考えられる順番の組み合わせは以下の6通りとなります。
- R Q 〇 〇
- R 〇 Q 〇
- R 〇 〇 Q
- 〇 R Q 〇
- 〇 R 〇 Q
- 〇 〇 R Q
※〇にはPまたはSのどちらかが入ります。
また、【3】よりPが4位になることはありません。よって、考えられる順番をすべて書き出すと以下のようになります。
- R Q P S
- R P Q S
- R P S Q
- R S P Q
- P R Q S
- P R S Q
- S R P Q
- P S R Q
- S P R Q
以上と選択肢ア・イ・ウを見比べていきます。
ア:RSPQ、SRPQのようにSがPよりも前にくるケースがあるので不適です。
イ:Rが4位になるケースはないので、正しいことがわかります。
ウ:SRPQ、SPRQのようにSが先頭になるケースがあるので不適です。
よって、答えはイ・・・(答)となります。
(2)こちらが最低限問題となります。(1)の組み合わせの中で1つに特定できる情報を選べばよいです。
カ:PRQS、PRSQなど、PRを含む順番は複数考えられるので不適です。
キ:RPSQ、PRSQなど、SQを含む順番は複数考えられるので不適です。
ク:QPを含む順番はRQPSだけです。
よって、答えはク・・・(答)となります。
以上のように推論の最低限問題では情報・条件から考えられるパターンをしらみつぶしに調べることが多く、時間がかかるのでご注意ください。
SPIで高得点を狙っている人は必ず対策しておきましょう。
※「SPIの推論とは?すべてがわかる!時間足りない・苦手な人向けの対策方法も解説」もぜひ合わせてご覧ください。
🔽 本にも載ってない極秘情報 🔽
SPIで最低限問題が出題されたら高得点?
テストセンター型のSPIには高得点指標(=自分が高得点を取れたかどうかの目安)が存在します。
※詳しくは「SPIの高得点目安・指標は?点数や正答率を知る方法」をご覧ください。
SPIの非言語の高得点指標ですが、出題された問題のうち推論問題が5〜6割以上を占めていれば高得点である可能性が非常に高いです。
そして、推論問題のうちチェックボックス形式の問題が出題されたら、さらに高得点である可能性が高いです。
チェックボックス形式の問題とは、上記でご紹介した最低限問題の例題のように「該当するものをすべて選びなさい」という指示がある問題のことです。
1つでも間違うと不正解になってしまうので難易度が高いです。
※「SPIのチェックボックスとは?例題で解説!出たら点数高い?」もぜひ参考にしてください。
そして、チェックボックス形式の問題だけでなく最低限問題も出題されたら、最高点に近い点数である可能性が高いです。
テストセンター型のSPIの結果は使い回しができるので、非言語で最低限問題が出題された場合はその結果を使い回すようにするとよいでしょう。
※テストセンターにおける使い回しの詳細は「SPIのテストセンターとは?対策・予約方法から時間・服装まで完全解説!練習問題付き」をご覧ください。
【SPI】最低限問題の練習問題
最後に最低限問題の練習問題をご用意しました。
SPIで高得点を狙っている人はぜひチャレンジしてみてください。
【練習問題1】
以下のような2階建てアパートにP、Q、R、S、T、Uの6人が1人1部屋ずつ住んでいる。空き部屋は各階に1つずつあり、6人の部屋割りについて以下4つのことがわかっている。
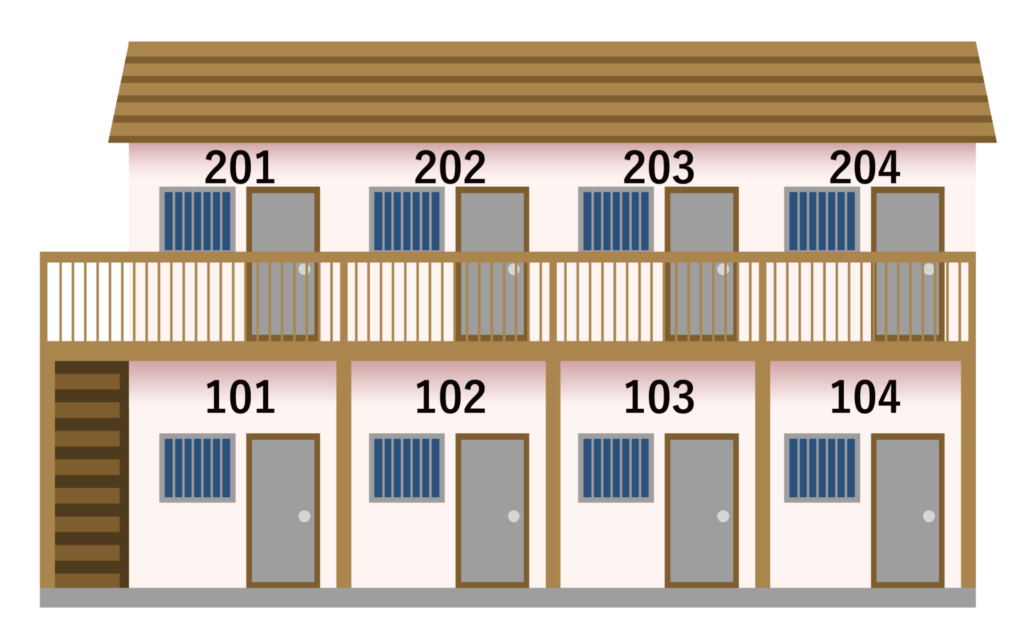
【1】202は空き部屋である。
【2】Pの隣にはSが住んでいる。
【3】Pの真下にはQが住んでいる。
【4】Tは端の部屋には住んでおらず、一方の隣は空き部屋である。
このとき、各問に答えよ。
(1)次の推論ア・イ・ウについて、必ずしも誤りとは言えないものはどれか。該当するものをすべて選びなさい。
ア:RはUの隣に住んでいる。
イ:空き部屋の真下も空き部屋である。
ウ:Tは2階に住んでいる。
(2)最も少ない情報で6人の部屋割りがすべてわかるようにするには【1】〜【4】のほかに、次のカ・キ・クのどの情報を加えればよいか。該当するものをすべて選びなさい。
カ:Rの真下は空き部屋である。
キ:Rは端に住んでいる。
ク:Uは103に住んでいる。
【解答&解説】
(1)【1】〜【4】より、P・Q・S・Tの部屋割りは以下の4通りになります。
※「ー」にはRまたはUが入ります。
| ー | 空き部屋 | P | S |
| 空き部屋 | T | Q | ー |
| 空き部屋 | ー | S | P |
| ー | T | 空き部屋 | Q |
| 空き部屋 | ー | S | P |
| 空き部屋 | ー | T | Q |
| 空き部屋 | ー | S | P |
| 空き部屋 | T | ー | Q |
以上の4パターンとア・イ・ウを見比べていきます。
ア:以上4つのパターンいずれも「ー」が隣り合っていないので、RとUが隣り合うことはありません。よって、アは不適となります。
イ:102と202が空き部屋になる可能性はあります。よって、イは必ずしも誤りとは言えません。
ウ:Tは必ず1階になっています。なのでウは不適です。
以上より、答えはイ・・・(答)となります。
(2)最低限問題となります。
カ:Rの真下が空き部屋になる部屋割りは上記より2通りあることがわかります。よって、カは不適となります。
キ:Rはどの部屋割りでも端になる可能性があります。よって、キは不適となります。
ク:Uが103に住むパターンは上記より1通りしかないことがわかります。なので、この情報を加えれば6人の部屋割りは確定します。
以上より、答えはク・・・(答)となります。
【練習問題2】
T、U、V、W、X、Y、Zの7人の性別について、以下2つのことがわかっている。
【1】T、V、W、Xの4人とZの性別は異なる。
【2】Uは女性である。
このとき、各問に答えよ。ただし、性別は男性と女性の2つしかないものとする。
(1)以下ア・イ・ウのうち、必ず正しいと言えるものはどれか。該当するものをすべて選びなさい。
ア:Zが男性の場合、男性の人数は2人以下である。
イ:Zが女性の場合、女性の人数は2人以下である。
ウ:YとZが同性の場合、男性と女性の人数の差は2人以下である。
(2)最も少ない情報で7人の性別を確定するためには、【1】と【2】の情報のほかに、以下のカ・キ・クのうち、どれが加わればよいか。該当するものをすべて選びなさい。
カ:男性の方が多い。
キ:UとYは同性、UとZは異性である。
ク:UとZは同性、UとVは異性である。
【解答&解説】
(1)ア:T、V、W、Xの4人とZ(男性)の性別が異なるので、T、V、W、Xは女性となります。
Uも女性なので、女性が7人中5人となります。つまり、男性は2人以下となるので必ず正しいことがわかります。
イ:T、V、W、Xの4人とZ(女性)の性別は異なるので、T、V、W、Xの4人は男性となります。
Uは女性で、Yは不明です。よって、女性は2人または3人となるので必ず正しいとは言えません。
ウ:仮にYが男性だとするとZも男性になります。
T、V、W、XとUが女性なので、女性5人、男性2人となります。人数の差は3人となるので、必ず正しいとは言えません。
よって、答えはア・・・(答)となります。
(2)カ:同性であるT、V、W、Xの4人は男性に確定します。UとZは女性に確定します。Yは不明です。
キ:Uは女性なので、Yも女性となります。ZはUと異性なので、Zは男性となります。Zと異性であるT、V、W、Xの4人は女性となります。よって、すべての性別が確定できます。
ク:UとZの2人は女性となります。Vは女性のUと異性なので、T、V、W、Xは男性となります。Yは不明です。
以上より、答えはキ・・・(答)となります。
今回はSPIの最低限問題とは何かについて解説していきました。
例題や練習問題の通り、最低限問題は難易度が高いことがお分かりいただけたかと思います。必ず事前に勉強・対策をしておきましょう。


