
SPIでは受検方式問わず場合の数が頻出です。
場合の数の問題は正解の確信がなかなか持てない問題なので、難しいと感じる人も多いです。
本記事では本番のSPIで出題される問題の難易度に近い場合の数の練習問題を15問ご用意しました。
SPIを受検予定の就活生や転職活動中の社会人はぜひ解いてみてください。
※「SPIで場合の数は頻出!解き方のコツと出題パターンを完全網羅!練習問題付き」もぜひ合わせてご覧ください。
ちなみにですが、SPIにはたった3時間の勉強でSPIが通過してしまう勉強法があります。
これさえあれば限りなく少ない努力で内定に大きく近づきます。
これは私が100回以上ものSPI受検を通して生み出した、どの本にも載っていない超コスパの良い究極の勉強法です。
興味のある人はぜひ以下のボタンからその方法をチェックしてみてください。
【SPI】場合の数の練習問題
では早速、場合の数の練習問題をご紹介します。
すべての問題に解答・解説を付けています。
※SPIの練習問題433問をすべて無料で掲載している記事もぜひ参考にしてください。
【練習問題1】
1から4までの数字を使って3桁の整数を作とき、320より大きい数は何通り作れるか。ただし、同じ数字を何回使ってもよいものとする。
【解答&解説】
百の位の数が3の場合と4の場合で分けて考えます。
百の位の数が3の場合、
- 十の位:2、3、4の3通り
- 一の位:1、2、3、4の4通り
なので、合計で3×4=12[通り]です。
百の位が4の場合、
- 十の位:1、2、3、4の4通り
- 一の位:1、2、3、4の4通り
なので、合計で4×4=16[通り]です。
よって答えは12+16=28[通り]・・・(答)となります。
【練習問題2】
1、2、3、4、5のカードが1枚ずつ、合計5枚ある。これらのカードを使って5桁の整数を作るとき、1と2が隣り合っている整数は何通り作れるか。
【解答&解説】
1と2をまとめて1枚のカードとみなし、4枚のカードの並べ方が何通りあるかを求めると、4×3×2×1=24[通り]です。
1と2の順番は「12」の場合と「21」の場合の2通りがあるので、答えは24×2=48[通り]・・・(答)となります。
【練習問題3】
数学が4問、英語が3問出題される試験があり、受験者は全7問の中から4問を選択して回答する。少なくとも数学から1問、英語から1問を選択する場合、問題の選び方は全部で何通りあるか。
【解答&解説】
問題の内訳には
(数学、英語)=(4、0)(3、1)(2、2)(1、3)
の4通りがあります。
このうち、(数学、英語)=(4、0)以外はすべて「少なくとも数学から1問、英語から1問を選択」があてはまります。
よって、すべての場合の数から1を引けば良いことがわかります。
すべての場合の数=7C4=7C3=(7×6×5)/(3×2×1)=35[通り]なので、答えは35-1=34[通り]・・・(答)となります。
※C(組み合わせ)の計算方法がわからない人は「SPIの組み合わせの公式と順列との違いをわかりやすく解説!練習問題付き」をご覧ください。
【練習問題4】
P、Q、R、S、Tの5つの神社があり、3日間ですべての神社を訪れる計画を立てる。1日目に2ヶ所、2日目に1ヶ所、3日目に2ヶ所訪れる場合、何日目にどこを訪れるか、その組み合わせは全部で何通りあるか求めよ。
【解答&解説】
1日目には5つの神社から2ヶ所を選ぶので、5C2=10[通り]の組み合わせがあります。
2日目は残りの3ヶ所から1ヶ所を選ぶので、3C1=3[通り]です。
3日目は自動的に残りの神社が選ばれます。
よって答えは10×3=30[通り]・・・(答)です。
【練習問題5】
A、B、C、D、Eの5人を縦一列に並ぶ5席に座らせる。Dより前にBがいて、Dより後ろにCがいる並べ方は何通りあるか。
【解答&解説】
5人の並び方は5×4×3×2×1=120[通り]ですね。
B・C・Dの並び方は3×2×1=6[通り]です。
しかし、B・C・Dの並び方はB→C→Dの1通りに確定しているので、答えは120÷6=20[通り]・・・(答)となります。
【練習問題6】
サイコロAとサイコロBを同時に振った。出た目の積が5の倍数になる組み合わせは何通りあるか求めよ。ただし「Aが1でBが6」と「Aが6でBが1」は別の組み合わせとして考えるものとする。
【解答&解説】
出た目の積が5の倍数になるのはサイコロAかBに5の目が出たときです。
Aが5のときはBが1〜6の6通りです。
Bが5のときはAが1〜6の6通りですが、ダブっている(A、B)=(5、5)の1通りを除くので、5通りです。
よって答えは6+5=11[通り]・・・(答)となります。
※SPIのサイコロ問題の解き方について詳しく解説した記事もぜひ参考にしてください。
【練習問題7】
箱の中に赤・緑・青のボールがたくさん入っている。この中から5個のボールを選ぶとき、選び方は全部で何通りあるか。
【解答&解説】
選んだ5個のボールを赤・緑・青の順に並べ、色と色の間を仕切り線で以下のように区切ってみます。
【例】
- 赤赤 | 緑 | 青青(赤2個、緑1個、青2個)
- | 緑緑緑 | 青青(赤0個、緑3個、青2個)
- | | 青青青青青(赤0個、緑0個、青5個)
つまり、この問題は2本の仕切り線と5個のボールという「合計7ヶ所の中から2ヶ所を選ぶ組み合わせ」の問題と同じになります。
よって答えは7C2=21[通り]・・・(答)となります。
【練習問題8】
男性3人、女性3人からなるグループがある。6人全員が輪になって並ぶ場合、並び方は何通りあるか。
【解答&解説】
全員が1つずつ席がずれても順番は変わらないことに注目します。
1つの席順につきこのような重複が6つあるので、6P6を6で割れば良いことがわかります。
よって答えは6P6 ÷ 6=5×4×3×2×1=120[通り]・・・(答)となります。
【練習問題9】
表裏のあるコインを7回投げた。裏が5回以上出るような表裏の出方は何通りあるか求めよ。
【解答&解説】
7回のうち、5回裏が出る出方は7C5=21[通り]です。
7回のうち、6回裏が出る出方は7C6=7[通り]です。
7回のうち、7回裏が出る出方は1通りです。
よって答えは21+7+1=29[通り]・・・(答)となります
【練習問題10】
P・Q・R・Sの4つのサイコロがある。P・Q・R・Sの順に1回ずつサイコロを振ったとき、Pが他の3つのサイコロよりも大きい目かつQ・R・Sが同じ目となるような組み合わせは何通りあるか。
【解答&解説】
問題文は1〜6の6つの整数にP>QRSという大小関係を満たす2つの整数の組み合わせは何通りあるかという意味なので、答えは6C2=15[通り]・・・(答)となります。
【練習問題11】
以下の図形を3色で塗り分けるとき、色の塗り方は何通りあるか。ただし、線で隣合う領域には同じ色が使えないものとする。また、3色のうち使わない色があってもよいものとする。
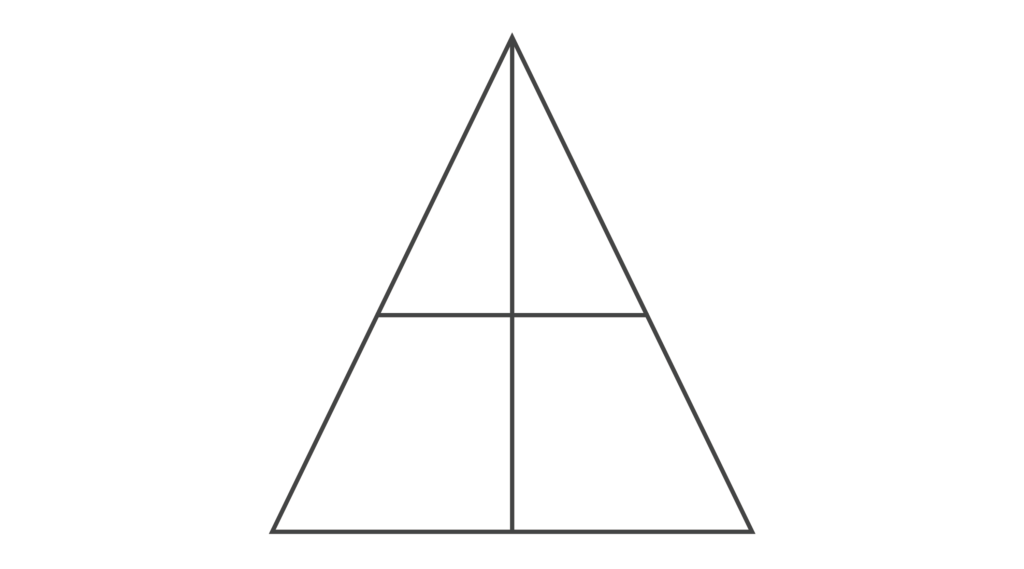
【解答&解説】
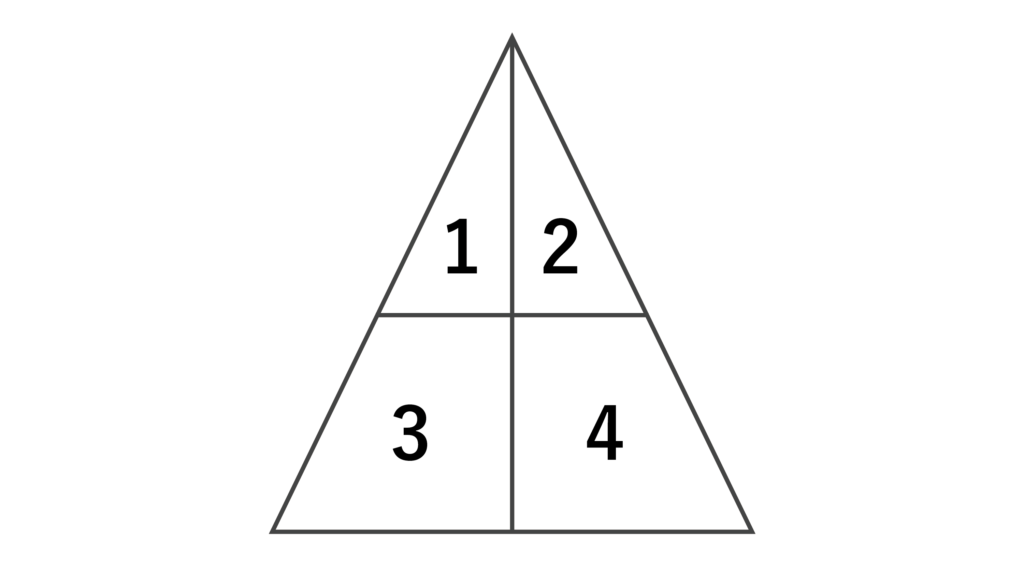
2色で塗り分ける場合、2色では以下図の1&4と2&3を塗り分けるパターンだけです。
3色から2色を選んで並べる順列と考えることができるので、3P2=6[通り]です。
3色で塗り分ける場合、以下図の1&4、2、3の3箇所に3色、または2&3、1、4の3箇所に3色を塗る2つの場合なので、3色を3箇所に並べる順列を2倍して、3P3 × 2=12[通り]です。
よって答えは6+12=18[通り]・・・(答)となります。
【練習問題12】
1から5までの数字を使って整数を作る。このとき、4桁の偶数は何通り作れるか。ただし、同じ数字を重複して使うことはできないものとする。
【解答&解説】
偶数の場合、一の位は2か4の2通りになります。
十の位は残り4つの数から1つを選ぶので4通りです。
百の位は残り3つの数から1つを選ぶので3通りです。
千の位は残り2つの数から1つを選ぶので2通りです。
よって答えは2×4×3×2=48[通り]・・・(答)となります。
【練習問題13】
男性5人、女性の3人のグループがある。この中から男女合わせて5人を選ぶとき、女性が少なくとも1人は含まれるように選ぶ場合、選び方は何通りあるか。
【解答&解説】
すべての場合の数から「女性が1人も含まれない(=全員が男性)」の場合の数を引けば良いです。
すべての場合の数=8C5=56[通り]です。
「女性が1人も含まれない(=全員が男性)」の場合の数は1通りです。
よって答えは56-1=55[通り]・・・(答)となります。
【練習問題14】
白いボールが4個と黒いボールが3個ある。これらのボールの中から4個を取り出して一列に並べる場合、並べ方は何通りあるか。
【解答&解説】
- 白1、黒3の場合=4C1=4[通り]
- 白2、黒2の場合=4C2=6[通り]
- 白3、黒1の場合=4C3=4[通り]
- 白4、黒0の場合=1[通り]
よって答えは4+6+4+1=15[通り]・・・(答)です。
【練習問題15】
リンゴ2個、ミカン2個、ブドウ1個をA・B・C・D・Eの5人に1個ずつ配る。AとBに同じ果物を配る場合、何通りの配り方があるか求めよ。
【解答&解説】
AとBにリンゴを配る場合、残りの3人のうち1人にブドウを配れば、他の2人は自動的にミカンになります。
その組み合わせは3C1=3[通り]です。
AとBにミカンを配る場合も同様に3通りなので、答えは3+3=6[通り]・・・(答)となります。
🔽 本にも載ってない極秘情報 🔽
今回はSPIで頻出分野の1つである場合の数の練習問題を取り上げました。
SPIで高得点を狙っている人は順列や組み合わせの違いなどに注意しながら、重点的に対策を行いましょう。


