
SPIの非言語(計数・数学)では流水算が出題範囲に含まれていますが、出題頻度としてはかなり低いので優先度を高めて勉強・対策する必要は特にないでしょう。
※「SPIとは?対策方法や問題・例題をすべて紹介!適性検査SPIはこれで完璧だ!」もぜひ合わせてご覧ください。
しかし、今後SPIで流水算の問題が新たに追加される可能性がないとは言い切れません。
そこで今回はSPIのことを知り尽くしているSPIマスターである私カズマがSPIで出題される流水算の解き方について例題や図解を使ってわかりやすく解説していきます。
流水算の公式や比を使った解き方についても解説していくので、数学が苦手な就活生や転職活動中の社会人はぜひ参考にしてください。
※「SPIの非言語(数学)を完全解説!対策方法やできない人でも点数を上げる方法!問題もご紹介」もぜひ合わせてご覧ください。
ちなみにですが、SPIにはたった3時間の勉強でSPIが通過してしまう勉強法があります。
これさえあれば限りなく少ない努力で内定に大きく近づきます。
これは私が100回以上ものSPI受検を通して生み出した、どの本にも載っていない超コスパの良い究極の勉強法です。
興味のある人はぜひ以下のボタンからその方法をチェックしてみてください。
目次
SPIの流水算を解くために必要な公式
流水算とは船が川を上ったり下ったりすることを想定し、そのときの川の流れの速さや船の速度などを計算する問題です。
流水算では以下3つの公式を必ず覚えておく必要があります。
1:速度に関する公式
1つ目は速度に関する公式です。流水算では速度の計算を行うので、速度に関する知識がないとそもそも問題を解くことができません。
具体的には距離(mやkm)を換算したり、速度(m/分やkm/時)を換算したり、距離や速度から所要時間を求めたりする能力が必要となります。
SPIで暗記必須の速度に関する公式(き・は・じの法則など)の詳細は「【SPI】速度算の練習問題18問!コツや解き方・公式・計算方法を完全解説!」をご覧ください。
2:船が川を下りるときの船の速度
静水時(=水の流れが全くない状況)の速度=a[km/時]である船が、速さb[km/時]で流れている川を下りることを想定します。
このとき、船の速度は川の流れの速さの分だけ加速されるので(a+b)km/時となります。
図にすると以下のようになります。
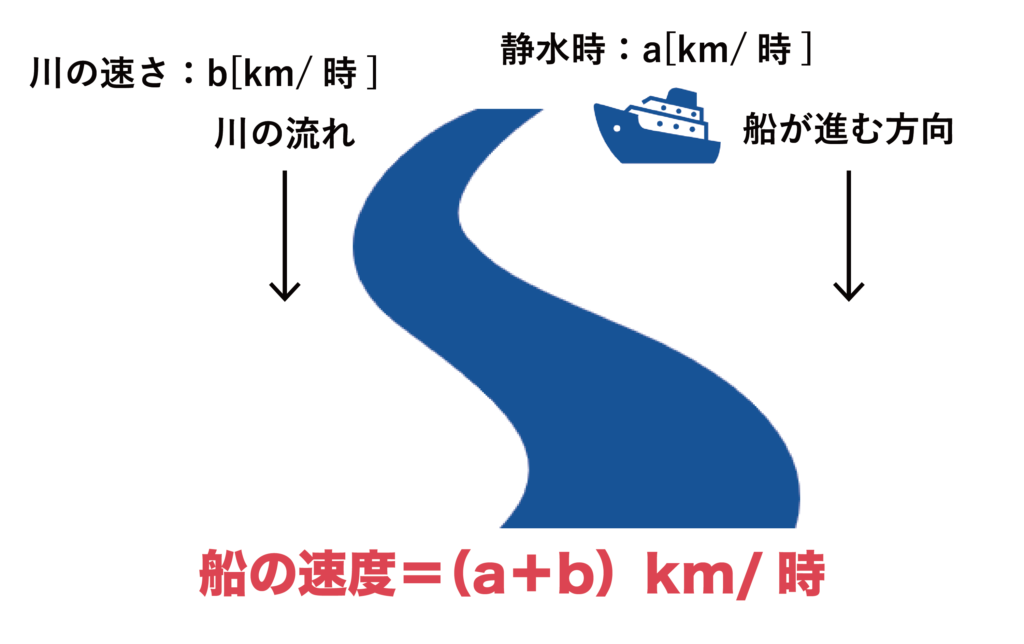
川の流れに沿って進むときは、川の流れの速さの分だけ加速されることをしっかり頭に入れておきましょう。
3:船が川を上るときの船の速度
逆に、船が川を上るときは川の流れの速さの分だけ船の速度は遅くなります。
静水時の速度=a[km/時]である船が、速さb[km/時]で流れている川を上ることを想定した場合、船の速度は(a-b)km/時となります。
図にすると以下のようになります。
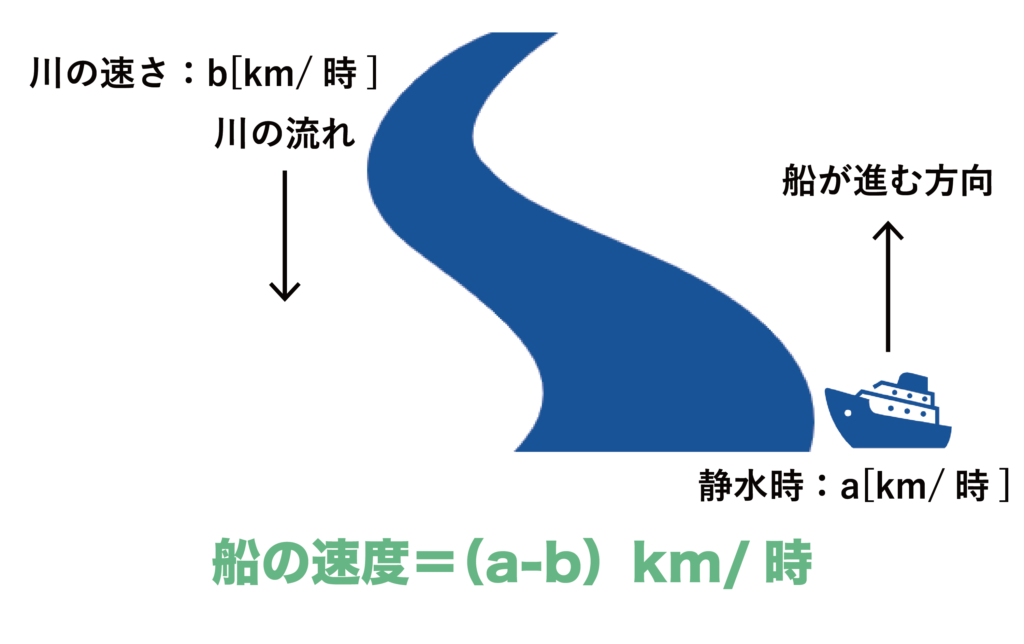
船の速度の方が川の流れの速さよりも早くないと川を上ることができません。
つまり、船の速度>川の流れの速さなのでa-bとなります。b-aとしてしまうと、b-aはマイナスの値になり、速度として不適になるのでご注意ください。
【SPI】流水算の例題と解き方
以上でご紹介した流水算を解くために必要な公式を頭に入れた上で、以下の例題を解いてみましょう。
【例題】
静水時の速度=15km/時である船がある川を36km上るのに3時間かかった。このとき、川の流れの速さは何km/時か求めよ。
【解答&解説】
川の流れの速さ=a[km/時]とおいてみましょう。
今回は船が川を上るので、船の速度=15-a[km/時]となります。
距離=速さ(速度)×時間で求めることができるので、36=(15-a)×3という方程式を立てることができます。
すると、15-a=12となるのでa=3[km/時]・・・(答)が求まります。
以上の例題は流水算の非常に基本的な問題なので、必ず解けるようにしておきましょう。
🔽 本にも載ってない極秘情報 🔽
【SPI】流水算を比を使って解く方法
川の流れの速さ、船が上りと下りに要する時間から船の静水時の速度を知りたい場合は比を使って計算することも可能です。
では、例題で解説していきます。
【例題】
流れの速さが4km/時の川がある。この川を船で上ると5時間、下ると4時間かかることがわかっている。この船の静水時の速度は何km/時か求めよ。
【解答&解説】
例えばですが、川の距離(長さ)が20kmであるとしましょう。
すると、船は上りに5時間かかっているので、上り時の船の速度=4km/時であることがわかります。
同様に考えて下り時の船の速度=5km/時となります。
- 上りにかかった時間:下りにかかった時間=5:4
- 上り時の船の速度:下り時の船の速度=4:5
より、時間の逆比が速度の比になっていることがわかります。
流水算においては必ず時間の逆比=速度の比になります。
ここで、上り時の船の速度、下り時の船の速度、静水時の船の速度を線で表すと以下のようになりますね。
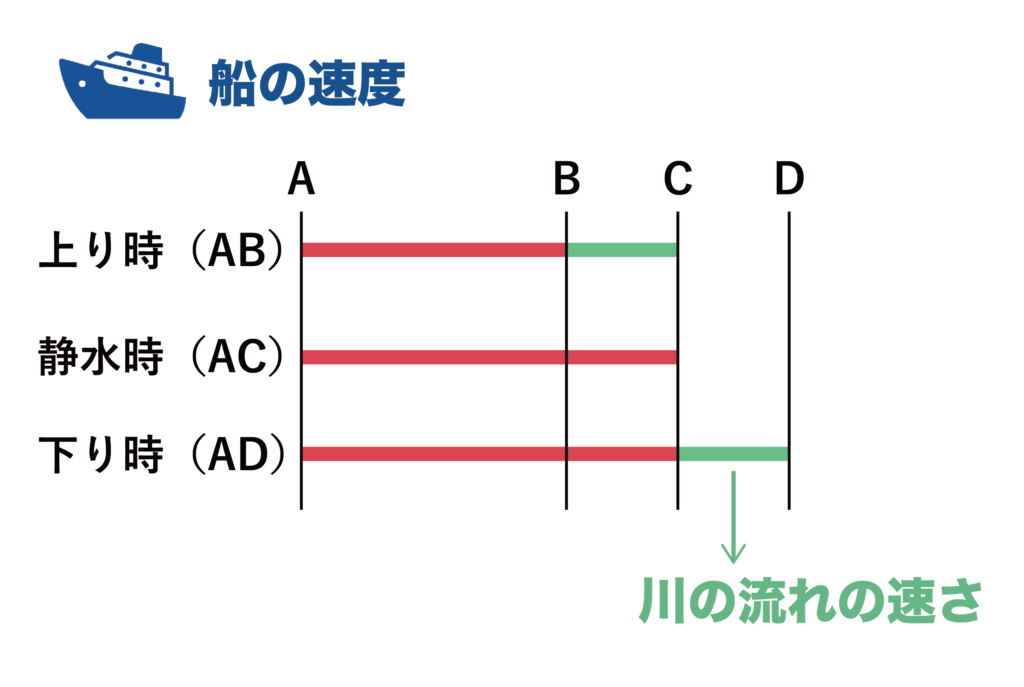
以上の図より、上り時の速度と下り時の速度の差は川の流れの速さ(4km/時)の2倍に相当する8km/時であることがわかります。
ここで、上りの速さをa[km/時]とすると(4×2):a=1:4という比の式を作ることができるので、内項の積=外項の積よりa=4×(4×2)=32[km/時]となります。
※内項の積=外項の積がわからない人は「【SPI】割合と比の練習問題20問!難しい?公式や解き方・コツもわかりやすく解説!」をご覧ください。
静水時の船の速度は上り時の速度に川の速さを加えればよいので、32+4=36[km/時]・・・(答)となります。
以上が比を使った流水算の解き方となります。難しいと感じる人は無理に比を使う必要はなく、連立方程式を使って解くことをおすすめします。
【別解:比を使わない解法】
比を使わない場合は以下の方法で解くことが可能です。
静水時の船の速度=a[km/時]、川の長さをb[km]とおいてみます。
すると、距離=速度×時間なので、
- b=(a-4)×5=5a-20・・・①
- b=(a+4)×4=4a+16・・・②
という連立方程式を立てることができます。
①-②より、0=a-36となるのでa=36[km/時]・・・(答)であることがわかります。
※ちなみにですが、川の長さはa=36を①に代入してb=(36-4)×5=160[km]となります。
※連立方程式の解き方がわからない人はSPIで絶対必要な方程式について解説した記事をご覧ください。
SPIにおける流水算の出題頻度と難易度
冒頭でも解説した通り、SPIの非言語(計数・数学)において流水算は出題範囲に含まれていますが、出題頻度としてはかなり低いので優先度を高めて勉強・対策する必要は特にありません。
ただし、SPIで高得点を狙う必要がある人は必ず流水算も勉強・対策をしてください。
※SPIの高得点目安・指標について詳しく解説した記事もぜひ参考にしてください。
※SPIでは4つの受検方式(WEBテスティング、テストセンター、ペーパーテスト、インハウスCBT)がありますが、全ての受検方式で流水算は出題範囲に含まれています。
※SPIのテストセンターとは何かについて詳しく解説した記事もぜひ参考にしてください。
流水算を解くためには上記でも解説した通り、速度に関する知識が必要です。
SPIでは速度算も出題範囲に含まれており、速度算は出題頻度が高いので勉強・対策は必須なのでご注意ください。
SPIの勉強をする時間がなかなか取れない就活生や転職活動中の社会人は流水算よりも速度算の勉強・対策に時間を使うことをおすすめします。
※「【SPI】転職・中途採用の対策法や問題・通過率などをSPIマスターが完全解説」もぜひ参考にしてください。
【SPI】流水算の練習問題
最後に流水算の練習問題をご用意しました。すべて基本的な問題なので全問解けるようになるまでしっかりと復習しましょう。
※もっとたくさんの問題を解きたい人は「【SPI】流水算の練習問題15選!本番で使える超便利なテクニックもご紹介!」も合わせてご覧ください。
【練習問題1】
ある船が8840mの川を上るのに34分、下るのに26分かかった。 この船の静水時の速度と川の流れの速さはそれぞれ何m/分か求めよ。
【解答&解説】
船の静水時の速度をa[m/分]、川の流れの速さをb[m/分]とします。
すると、
- 8840=(a-b)×34=34a-34b・・・①
- 8840=(a+b)×26=26a+26b・・・②
という連立方程式が立てられますね。
①を13倍すると114920=442a-442b・・・③となります。
②を17倍すると、150280=442a+442b・・・④となります。
すると、④-③より35360=884bとなるのでb=40[m/分]・・・(答)となります。
b=40を①に代入して、8840=34a-34×40となるので、34a=10200よりa=300[m/分]・・・(答)となります。
【練習問題2】
静水時における速度が20km/時の船が川の上流まで往復するのに6時間かかった川の流れの速さが5km/時だったたとき、川の下流から上流までの距離は何kmか求めよ。
【解答&解説】
時間=距離÷速さで求めることができるのでした。
船が下流から上流に移動するとき、船の速度=20-5=15km/時ですね。
一方で船が上流から下流に移動するとき、船の速度=20+5=25km/時です。
川の下流から上流までの距離をP[km]とおくと、
P/15+P/25=6という方程式を立てることができるので、両辺を75倍(15と25の最小公倍数)して、
5P+3P=6×75より8P=450となるので、P=56.25[km]・・・(答)となります。
🔽 本にも載ってない極秘情報 🔽
いかがでしたか?
今回はSPIの流水算の公式や解き方について解説をしていきました。
繰り返しにはなりますが、SPIでは流水算の出題頻度が低いので時間がない人は重点的に勉強・対策をする必要はありません。
しかし、流水算でも使用する速度算は時間がない人でも必ず勉強・対策するようにしましょう。最後までお読みいただき、ありがとうございました。


