
SPIの非言語(数学・計数)では場合の数が出題範囲に含まれています。
場合の数は苦手な人も多いですが、SPIで高得点を狙うのであれば勉強・対策は必須です。
※「SPIとは?対策方法や問題・例題をすべて紹介!適性検査SPIはこれで完璧だ!」もぜひ合わせてご覧ください。
本記事ではSPIを100回以上も受検し、SPIについて日本で一番熟知しているSPIマスターの私カズマがSPIで出題される場合の数のコツについて解説した後、場合の数の問題パターンをすべてご紹介していきます。
SPIを受検予定の就活生や転職活動中の社会人はぜひ参考にしてください。
※「SPIの非言語(数学)を完全解説!対策方法やできない人でも点数を上げる方法!問題もご紹介」もぜひ合わせてご覧ください。
ちなみにですが、SPIにはたった3時間の勉強でSPIが通過してしまう勉強法があります。
これさえあれば限りなく少ない努力で内定に大きく近づきます。
これは私が100回以上ものSPI受検を通して生み出した、どの本にも載っていない超コスパの良い究極の勉強法です。
興味のある人はぜひ以下のボタンからその方法をチェックしてみてください。
目次
【SPI】場合の数の例題とコツ
まずはSPIで出題される場合の数の例題を2つご紹介します。
【例題1】
男子3人、女子4人から3人を選びたい。選んだ3人のうち、女子が1人だけ含まれる選び方は全部で何通りあるか求めよ。
【解答&解説】
女子が1人だけ含まれるということは、残り2人は男子になりますね。
男子3人から2人を選ぶ方法=3C2=3C1=3[通り]です。
そのおのおのに対して、女子4人から1人を選ぶ方法は4C1=4[通り]あるので、求める答えは3×4=12[通り]・・・(答)となります。
【例題2】
囲碁部には9人の部員がいる。この9人の中から部長と副部長を1人ずつ選ぶとき、選び方は全部で何通りあるか求めよ。
【解答&解説】
9人の中から部長を選ぶ選び方は9通りです。
残った8人の中から副部長を選ぶ選び方は8通りです。
よって答えは9×8=72[通り]・・・(答)となります。
※9P2=9×8=72です。

以上がSPIで出題される場合の数の例題となります(難易度としてはかなり易しい問題です)
場合の数の問題を解くコツですが、それは組み合わせ(C)を使うのか順列(P)を使うのかを見極めることです。
SPIで出題される場合の数の問題では組み合わせ・順列の計算が登場するケースが多いです。
しかし、組み合わせを使うのか順列を使うのかを見極めるのが苦手な人も多いでしょう。
ポイントは並べる順番を考慮するかどうかです。考慮しない場合は組み合わせ、考慮する場合は順列となります。
先ほどの例題1では男子3人、女子4人から3人を選ぶという動作において選ぶ順番や並べる順番は考慮していません(問題文にそのような指示は書かれていません)
なので、順列ではなく組み合わせCの公式を使いました。
例題2では部長と副部長は区別されるものなので順列Pの公式を使いました。
組み合わせと順列の見極めは難しいですが、問題をたくさん解いて慣れていくしかありません。
時間に余裕のある人はぜひ場合の数の勉強・対策に時間をかけてみてください。
※SPIの組み合わせの公式と順列との違いをわかりやすく解説した記事もご用意しているので、ぜひ合わせてご覧ください。
【SPI】場合の数の出題頻度と難易度
SPIにはテストセンター、WEBテスティング、インハウスCBT、ペーパーテストという4つの受検方式がありますが、場合の数は4つすべての受検方式の出題範囲に含まれています。
※SPIのWEBテスティングを完全解説した記事もぜひ合わせてご覧ください。
また、出題頻度も高く、テストの中盤あたりでよく登場します。
SPIで出題される場合の数の難易度は少し高めです。組み合わせや順列の公式を知っていれば簡単に解けるような問題はほぼ出題されず、何かしらの工夫が必要な問題が多いです。
※「SPIは難しい?難しすぎる?難易度(レベル)を言語と非言語別に解説!苦手・苦手すぎる人がやるべきことは?」もぜひ参考にしてください。
場合の数は苦手とする人が多い分野ですし、難易度も少し高めなので勉強・対策の優先順位としてはそこまで高くありません。
SPIの対策に時間的余裕のある人は取り組むと良いでしょうが、余裕のない人は場合の数に対策の時間を割くよりも、速度算や損益算などに時間を割きましょう。
これらの分野は頻出かつ難易度もそこまで高くないので、勉強のコスパが非常に良いです。
※「【SPI】損益算の練習問題20選!コツと公式もわかりやすく解説!捨てるのはあり?」もぜひ参考にしてください。
🔽 本にも載ってない極秘情報 🔽
【SPI】場合の数の練習問題
最後にSPIで出題される場合の数の練習問題をご用意しました。
SPIでは組み合わせや順列だけでなく、その他の知識も活用した場合の数の問題が出題されるのでチェックしておきましょう。
※もっとたくさんの問題を解きたい人は「【SPI】場合の数の練習問題15選・わかりやすい解説も」を合わせてご覧ください。
不等式の活用
【問題】
りんごとみかんを合わせて15個購入することにした。ただし、りんごとみかんの個数について以下のような条件があるとする。
- りんごは6個以上購入する
- りんごの個数はみかんの個数の1.5倍以下となるようにする
このとき、りんごとみかんの個数の組み合わせは全部で何通りあるか求めよ。
【解答&解説】
りんごをa[個]、みかんの個数をb[個]購入するとします。
すると、問題文の条件より
- a+b=15・・・①
- a≧6・・・②
- a≦1.5b・・・③
となりますね。
①よりb=15-aなので、これを③に代入すると、a≦1.5(15-a)より、2.5a≦22.5よりa≦9・・・④となることがわかります。
すると、②と④より、6≦a≦9であることがわかります。
したがって、a=6、7、8、9となるので答えは4[通り]・・・(答)となります。

数字の組み合わせ
【問題】
0、1、2、3、4の5個の数字から異なる4個の数字を取って並べるとき、4桁の整数は何個作ることができるか答えよ。
【解答&解説】
千の位は0以外の1〜4から1個選べば良いので4通りあることがわかります。
そして、そのおのおのについて百、十、一の位は0を含めた残りの4個から3個を取る順列となるので、4P3=4・3・2=24[通り]となります。
よって答えは、4×24=96[通り]・・・(答)となります。
順列
【問題】
A、B、C、D、E、Fの6人を一列に並べる。先頭をA、最後尾をFにする場合、並べ方は何通りあるか求めよ。
【解答&解説】
AとFの位置は固定されているため、AとFを除く4人の並び方のみを考えれば良いです。
よって答えは、4P4=4×3×2×1=23[通り]・・・(答)となります。
席決め
【問題】
A、B、C、Dの4人で以下の図のように1〜6の番号が振られたテーブル席に座ることを考える。1にAが座り、BとCが向かい合う座り方は全部で何通りあるか求めよ。
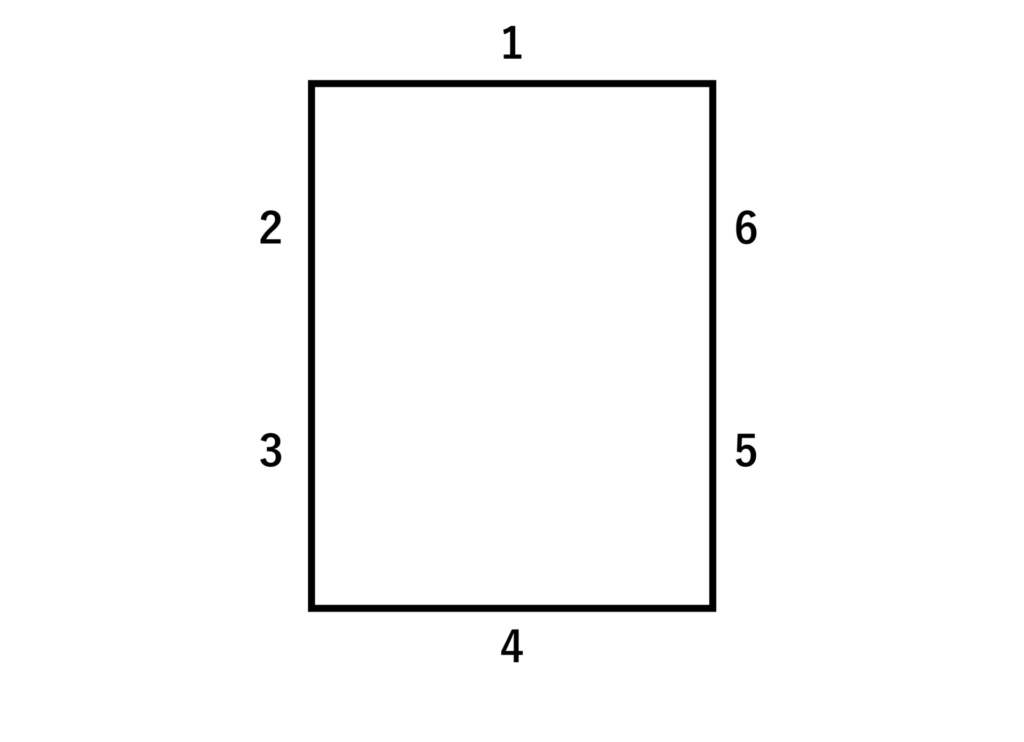
【解答&解説】
1にAが座ったとき、BとCが向かい合うのは(B、C)とすると(2、6)(6、2)(3、5)(5、3)の4通りですね。
この4通りについて残った3席からDが座る席を選ぶ方法が各3通りあるので、答えは4×3=12[通り]・・・(答)となります。
塗り分け
【問題】
以下の図のような長方形に色を塗ることを考える。このとき、赤・青・紫・緑から3色を選び、その3色で塗り分ける方法は全部で何通りあるか求めよ。ただし、線で隣り合う領域には同じ色は使えないものとし、3色すべてを使うものとする。

【解答&解説】
問題文の条件を満たすには、以下の図のようにまず1色で2つの領域を塗り、残り2色で1領域ずつ塗れば良いことがわかります。
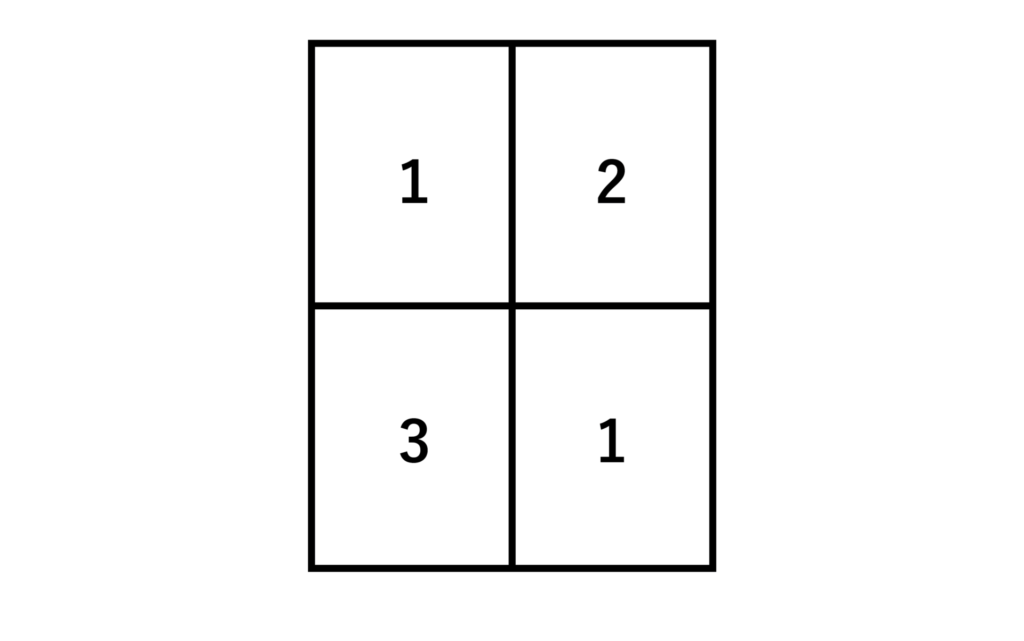
塗り分け方は、2つの領域を塗る色の選び方と同じなので3C1=3[通り]となります。
そして、4色から3色を選ぶ方法=4C3=4[通り]です。
よって、求める答えは3×4=12[通り]・・・(答)となります。
※SPIの塗り分け問題について詳しく解説した記事もぜひ合わせてご覧ください。
サイコロ
SPIではサイコロを活用した場合の数の問題も出題されます。
【問題】
サイコロを2個同時に投げるとき、出た目の数の積が5の倍数になる組み合わせは何通りあるか求めよ。
【解答&解説】
サイコロを2個投げる問題では、以下のような表を書くのがポイントです。
| 積 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 4 | 5 | 6 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 |
出た目の積が5になっているのは上記の表より、11[通り]・・・(答)あることがわかります。
※SPIのサイコロ問題の解き方について詳しく解説した記事もぜひ参考にしてください。

カード
【問題】
0、1、2、3、4のカードが1枚ずつ、計5枚ある。これらのカードから3枚を選び、1列に並べて3桁の整数を作る。このとき、320よりも大きい整数は何個作れるか求めよ。
【解答&解説】
320よりも大きい数になるのは百の位が4か3の場合です。
まずは百の位が4の場合を考えましょう。
百の位が4の場合、十の位は0〜3の4通りですね。一の位は十の位で使用した数字を除く3通りです。
よって、4×3=12[通り]であることがわかります。
続いて百の位が3の場合ですが、これは321、324、340、341、342の5通りですね。
よって答えは12+5=17[通り]・・・(答)となります。
コイン
【問題】
コインを7回投げるとき、裏が5回以上出るような裏表の出方は全部で何通りあるか求めよ。
【解答&解説】
7回のうち5回裏が出る出方=7C5=7C2=21[通り]ですね。
同様に考えて、7回のうち6回裏が出る出方=7C6=7C1=7[通り]です。
7回のうち7回裏が出る出方は明らかに1通りです。
よって答えは21+7+1=29[通り]・・・(答)となります。
円順列その1
円順列とは、いくつかのものや人を円形に並べる配列のことです。
【問題】
4人が手を繋いで円になるとき、並び方は全部で何通りあるか。
【解答&解説】
順列では4P4=24[通り]です。しかし、円形なので、4人をA・B・C・Dとすると、以下の4つの並びはすべて同じものとみなすことができます。
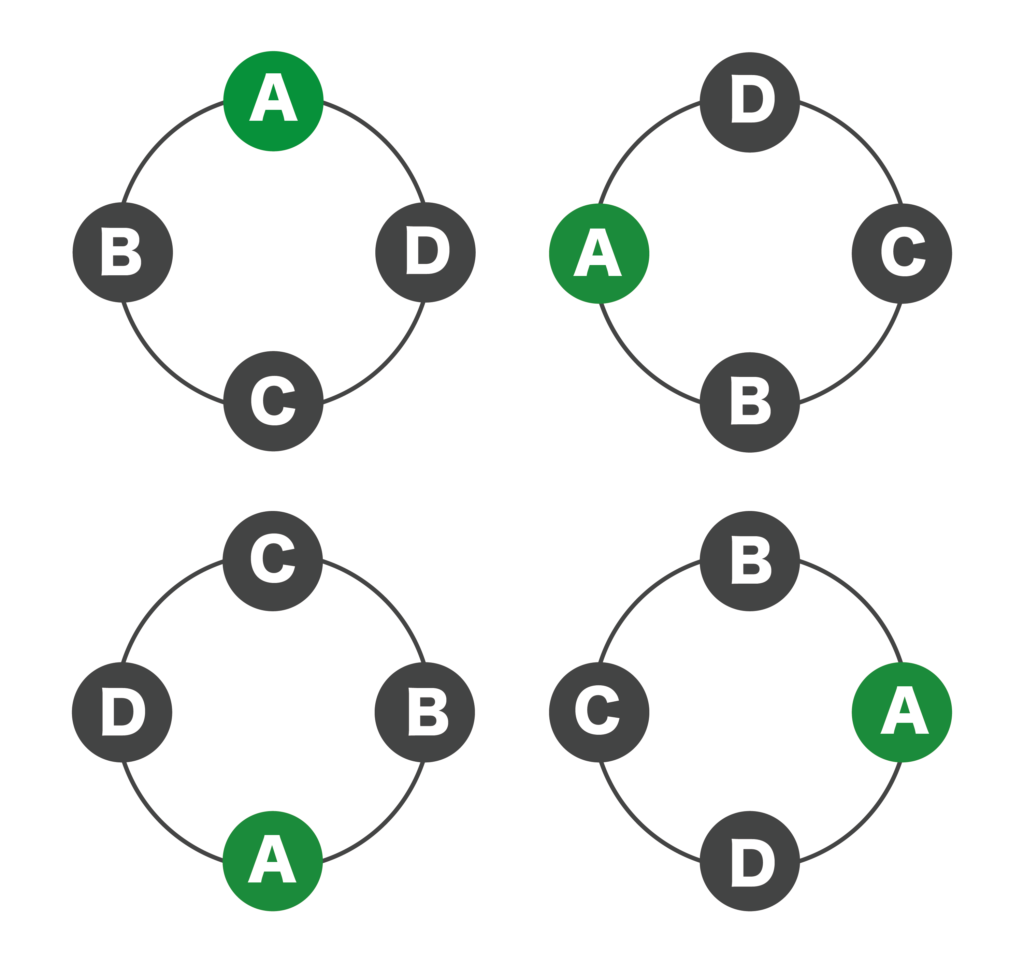
同じものを4回重複してカウントしているので、順列4P4を4で割る必要があります。
よって答えは、24÷4=6[通り]・・・(答)となります。
円順列その2
【問題】
異なる6個のコップがある。これらのコップを円形に並べる方法は全部で何通りあるか求めよ。
【解答&解説】
円順列では、円を回転させて並びが一致するものは同じであるとみなします。
詳しい説明は割愛しますが、異なるn個のものの円順列の総数=(n-1)!で求めることができます。
今回は6個のコップがあるので、求める答えは(6-1)!=5!=5×4×3×2×1=120[通り]・・・(答)となります。
※円順列について詳しく学びたい人は円順列とは何かについて解説した記事をご覧ください。
重複順列
【問題】
2、3、4を使ってできる5桁の奇数は全部で何個あるか求めよ。ただし、同じ数字を何回も使っても良いものとする。
【解答&解説】
奇数なので一の位は必ず3となります。
万、千、百、十の位それぞれに2、3、4の3通りの数字を当てはめることができるので、答えは34=81[個]・・・(答)となります。
重複組み合せ
【問題】
ある八百屋でトマト、レタス、タマネギが販売されている。この3種類の野菜の中から5つの野菜を購入するとき、全部で何通りの買い方があるか求めよ。ただし、1つも購入しない野菜があっても良いものとする。
【解答&解説】
「◯」と「|」を使ってトマト、レタス、タマネギをそれぞれ何個購入したかを表してみます。
例えば、
◯|◯◯|◯◯の場合、トマト=1個、レタス=2個、タマネギ=2個とします。
||◯◯◯◯◯の場合、トマト=0個、レタス=0個、タマネギ=5個とします。
すると、5つの「◯」と2つの「|」の順列の総数=3種類の野菜の中から5つの野菜を購入する買い方の総数となることがわかります。
よって求める答えは5+2C5=7C5=7C2=21[通り]・・・(答)となります。
🔽 本にも載ってない極秘情報 🔽
いかがでしたか?
今回はSPIで出題される場合の数を取り上げました。難易度が高い問題が多いので、時間があまりない就活生や転職活動中の社会人は場合の数の対策優先度は上げなくて良いですが、SPIの非言語(数学・計数)で高得点を狙っている人は必ず勉強・対策しておきましょう。
※「【SPI】転職・中途採用の対策法や問題・通過率などをSPIマスターが完全解説」もぜひ参考にしてください。


