
SPIでは塗り分けに関する問題が出題範囲に含まれていますが、WEBテスティングとインハウスCBTの受検方式で受検予定の人は勉強・対策する必要はありません。
しかし、テストセンターとペーパーテストの受検方式で受検予定の人は余裕があれば勉強しておいた方が良いでしょう(後ほど詳しく解説します)
※SPIのテストセンターとは何かについて詳しく解説した記事もぜひ参考にしてください。
本記事ではSPIについて日本トップレベルに詳しいSPIマスターの私カズマがSPIの塗り分け問題とはどんな問題なのかについて解説した後、塗り分け問題を解くコツや出題頻度・難易度などについても解説していきます。
ちなみにですが、SPIにはたった3時間の勉強でSPIが通過してしまう勉強法があります。
これさえあれば限りなく少ない努力で内定に大きく近づきます。
これは私が100回以上ものSPI受検を通して生み出した、どの本にも載っていない超コスパの良い究極の勉強法です。
興味のある人はぜひ以下のボタンからその方法をチェックしてみてください。
SPIの塗り分け問題とは?例題で解説
塗り分け問題と言ってもイメージがつかない人も多いかと思いますので、1問例題を解いてみましょう。
SPIでは以下のような塗り分け問題が出題されます。
【例題】
以下の図のような円において、隣り合う箇所を異なる色で塗り分けることを考える。このとき、赤・青・黒・黄から2色を選んで塗り分ける方法は全部で何通りあるか求めよ。ただし、円を回転させて一致する塗り方は同じものとみなす。
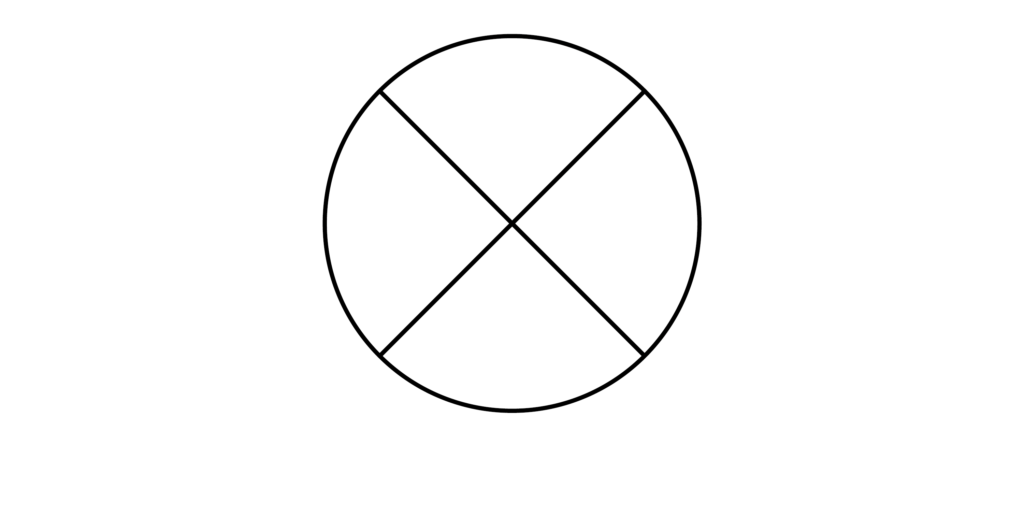
【解答&解説】
問題文に隣り合う箇所=異なる色という条件があるので、以下の図において1と2の色を決めると残りの2色(3と4)も自動的に決まりますね。
※例えば1=赤、2=青にした場合、3=赤、4=青が自動的に決まります。

よって、求める場合の数=4色から2色を選ぶ方法なので、4C2=6[通り]・・・(答)となります。
※Cの計算方法がわからない人はSPIの組み合わせの公式について解説した記事をご覧ください。
SPIの塗り分け問題を解くコツ・対策方法
塗り分け問題は解き方のイメージがつきにくい場合が多いため、苦手な人も多いですが、問題を解くコツとしては様々な解法パターンを頭に入れておくことです。
SPIでは応用問題や難易度が極端に高い問題は出題されません。ほとんどが基本的な問題となります。
なので、塗り分け問題に関しても数学の問題の難易度としては易〜中くらいです。
塗り分け問題は解き方のパターンがそこまで多くはないので、SPIの問題集や参考書に掲載されている塗り分け問題の解法をすべて頭に入れる(=暗記する)のが一番手っ取り早いです。
※おすすめのWEBテスティングの問題集をランキング形式でご紹介した記事もぜひ参考にしてください。
本記事では最後にSPIで出題される塗り分け問題に近い難易度の練習問題をご用意しているので、SPIの非言語(数学・計数)で高得点を狙っている人はこの練習問題の解法もすべて頭に入れておくと良いでしょう。
🔽 本にも載ってない極秘情報 🔽
SPIの塗り分け問題の出題頻度は?
SPIではテストセンターとペーパーテストでのみ塗り分け問題が出題範囲に含まれています。
WEBテスティング、インハウスCBTでは塗り分け問題は出題されませんのでご注意ください。
そして、テストセンターとペーパーテストにおける塗り分け問題の出題頻度は低いです。
※SPIのペーパーテストについて完全解説した記事もぜひ合わせてご覧ください。
本記事の筆者は今までに100回以上もSPIを受検しており、今でも月に1回はSPIを受検していますが、塗り分け問題に遭遇した経験はあまりありません。
また、先ほども解説した通り、塗り分け問題の勉強・対策をしっかりやろうと思うと、様々な解法パターンを頭に入れなければならないので時間がかかります。
つまり、塗り分け問題は出題頻度=低い、対策難易度=高い分野なので勉強のコストパフォーマンスとしてはかなり悪い印象です。
あまりSPIの勉強に時間が割けない就活生や転職活動中の社会人は塗り分け問題の勉強・対策にあまり時間を使わないように十分ご注意ください。
【SPI】塗り分け問題の練習問題
最後に塗り分け問題の練習問題をご用意しました。解答&解説も掲載しているので、非言語(数学・計数)で高得点を狙っている人はぜひチャレンジしてみてください。
※SPIの高得点目安・指標について詳しく解説した記事もぜひ参考にしてください。
【練習問題1】
以下の図のような円において、隣り合う箇所を異なる色で塗り分けたい。このとき、赤・青・オレンジ・黒から3色を選び、その3色すべてを使って塗り分ける方法は全部で何通りあるか求めよ。ただし、円を回転させて一致する塗り方は同じものとみなす。

【解答&解説】
隣り合う箇所が同じ色にならないように3色で塗り分けを行うには、まず1色で2箇所を塗り、残り2色は1箇所ずつ塗れば良いことがわかります(以下の図参照)
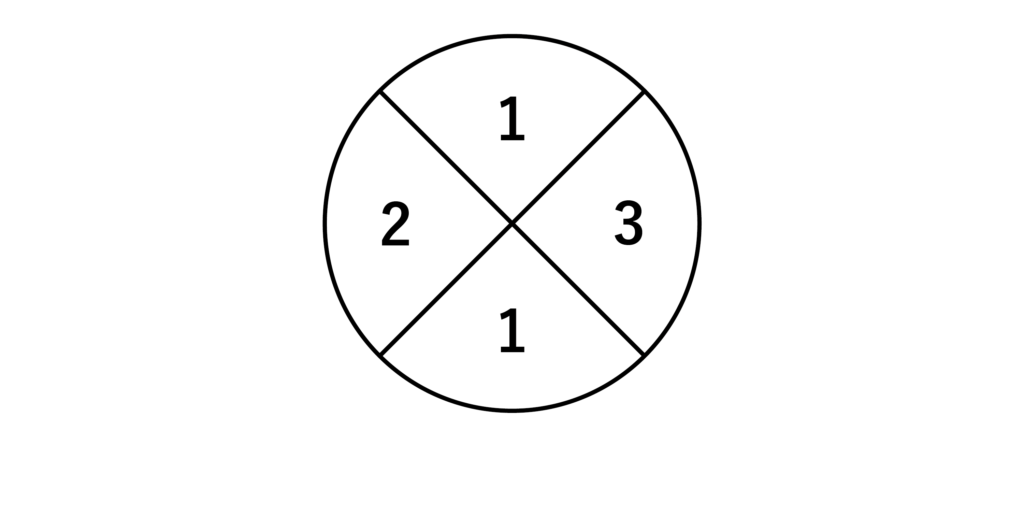
塗り分け方は、2箇所を塗る色の選び方と同じなので、3C1=3[通り]です。
また、4色から3色を選ぶ方法=4C3=4[通り]です。
よって、求める答えは3×4=12[通り]・・・(答)となります。
【練習問題2】
以下の図のように、正方形を各辺の中点で結んで5つの領域に分ける。隣り合った領域は異なる色で塗り分けるとき、異なる4色から2色を選んで塗り分ける方法は何通りあるか求めよ。ただし、回転して一致する塗り方は同じ塗り方と考える。
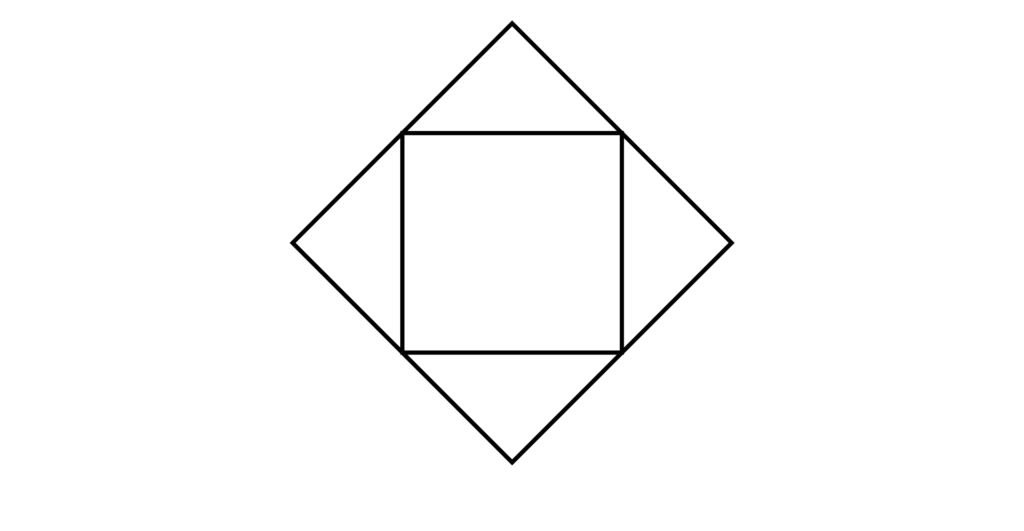
【解答&解説】
4色から2色を選び、以下の図の1、2の順に塗れば良いことがわかります。

よって、求める塗り分け方は4P2=4×3=12[通り]・・・(答)となります。
【練習問題3】
以下の図において、線で囲まれた領域すべてに色を塗ることを考える。赤・青・緑・紫の4色が使えるとき、色の塗り分け方は何通りあるか求めよ。ただし、線で隣り合う領域には同じ色は使えないものとする。
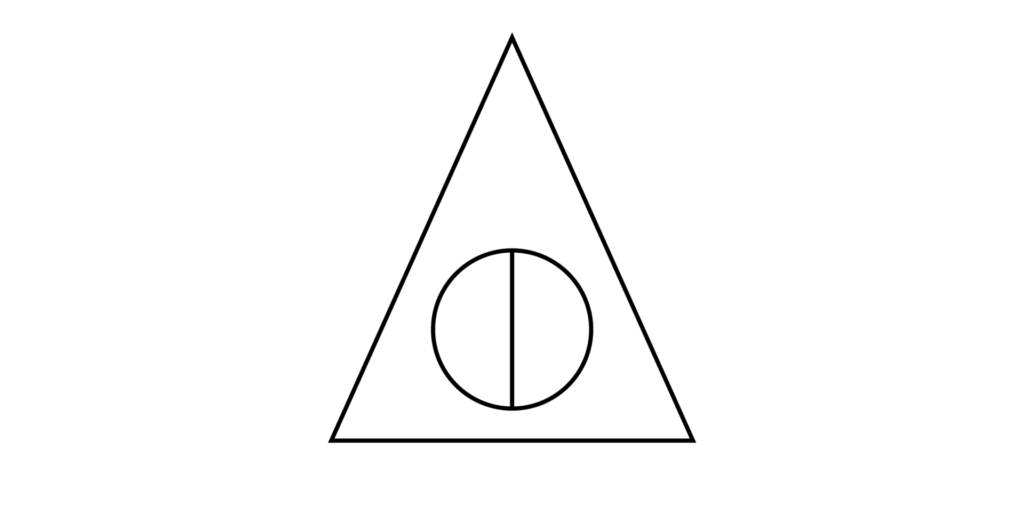
【解答&解説】
以下の図のように1〜3の3つの領域に分けてみます。

例えば1に赤を塗った場合、2と3には残りの3色から2色を選べば良いので3P2=6[通り]となりますね。
それが4色についても同様なので、求める塗り分け方は6×4=24[通り]・・・(答)となります。
🔽 本にも載ってない極秘情報 🔽
いかがでしたか?
今回はSPIの塗り分け問題について解説をしていきました。
例題や練習問題を見ていただくとおわかりいただけたかもしれませんが、塗り分け問題は解法のイメージが非常につきにくい問題です。
苦手だと感じた人は塗り分け問題には勉強・対策の時間を使いすぎないようご注意ください。


