
適性検査(WEBテスト)の一種であるSPIでは1本のロープ問題が出題されることがあります。
※「SPIとは?対策方法や問題・例題をすべて紹介!適性検査SPIはこれで完璧だ!」もぜひ合わせてご覧ください。
1本のロープ問題は推論問題の1つで、難易度は高くないので必ず正解しておきたいところです。
本記事ではSPIの受検回数100回超・日本で一番SPIに詳しい私カズマが、SPIで出題される1本のロープ問題の例題とその解き方についてわかりやすく解説していきます。
ちなみにですが、SPIにはたった3時間の勉強でSPIが通過してしまう勉強法があります。
これさえあれば限りなく少ない努力で内定に大きく近づきます。
これは私が100回以上ものSPI受検を通して生み出した、どの本にも載っていない超コスパの良い究極の勉強法です。
興味のある人はぜひ以下のボタンからその方法をチェックしてみてください。
【SPI】1本のロープとは?例題と解き方
では早速、SPIの非言語で出題される1本のロープの例題をご紹介します。
※SPIの非言語(数学)を完全解説した記事もぜひ参考にしてください。
制限時間は1分です。
【例題】
1本のロープにオレンジ、青、赤、紫の印が付けられているが、順番は不明である。それぞれの印の間の長さについて以下のことがわかっている。
ア:青と紫の間が一番長い
イ:オレンジと青の間は25cm、青と赤の間は40cm、赤と紫の間は20cmである
このとき、オレンジと紫の間は何cmか求めよ。
【解答&解説】
条件アより、青と紫がロープの端であることがわかります。

そして、条件イより、左から青→オレンジ→赤→紫の配置であることがわかります。図にすると以下のようになります。
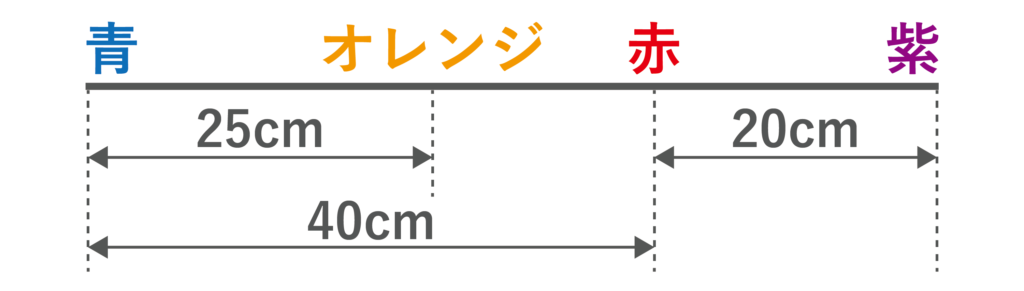
オレンジと赤の間は40-25=15[cm]なので、オレンジと紫の間は15+20=35[cm]・・・(答)となります。
【SPI】1本のロープのポイント
1本のロープ問題は推論問題の1種です。
SPIの推論は最も難しい分野と言われており、苦戦する人が多いです。
※詳しくは「SPIの難問(難しい問題)はどんな問題?分野と例題をご紹介」をご覧ください。
しかし、1本のロープ問題は推論の中で一番簡単な問題と言っても過言ではないので、必ず解けるようにしておきましょう。
解き方のコツは頭の中で考えるのではなく、与えられた情報をどんどん図にしていくことです。
例えば、上記の例題では条件アから以下のような図を作りました。

上記の例題に関して言えば、条件アから青と紫がロープの端であることに気づけるかどうかが最大のポイントです。
これにさえ気づければ、あとは条件イから簡単に問題が解けるはずです。
SPIの非言語で出題される推論は頭の中だけで考えると混乱しやすいので、必ず与えられた条件を図や式などに示す癖を付けておきましょう。
推論の具体的な対策方法やコツについては「SPIの推論問題の例題とコツ!難しい?捨てるべき人とそうでない人は?」に詳しくまとめているので、ぜひ参考にしてください。
練習問題
最後に1本のロープ問題に似たSPIの推論の練習問題をご用意しました。
※SPIの練習問題433問をすべて無料で掲載している記事もぜひ参考にしてください。
SPIを受検予定の就活生や転職活動中の社会人は1問1分を目安に解いてみましょう。
【練習問題1】
あるイベントで芸能人P、Q、R、Sの4人が1人ずつトークショーをすることになった。順番について以下のことがわかっている。
ア:QとRが続くことはない
イ:PはRの次である
ウ:SはQよりも後である
このとき、Qは何番目か。あてはまるものをすべて選びなさい。
- 1番目
- 2番目
- 3番目
- 4番目
【解答&解説】
ワンセットになる組み合わせから考えていきます。
条件イより、RPでワンセットとします(RとPの間には誰も入らない)
条件ウより、Q→Sとします(QとSの間には誰か入る可能性がある)
条件アより、QRPSではありません。
よって、QSRPまたはRPQSのどちらかになります。
以上より、答えは1・3・・・(答)です。
【練習問題2】
V、W、X、Y、Zの5人がスピーチをする順番をくじで決めた。それについて、次のことがわかっている。
ア:VはYの次である
イ:XはWの次だが、最後ではない
このとき、Zは何番目にスピーチするか。
【解答&解説】
条件アより、YVでワンセットです。
条件イより、W〇X〇でワンセットです。
アとイを組み合わせると「W〇XYV」しかあり得ません。
よって、Zは2番目・・・(答)となります。
【練習問題3】
P、Q、R、S、T、Uの6人はX小学校の1年〜6年それぞれの担任である。それぞれの担任が持つ学年について、以下のことがわかっている。
ア:PはQより4学年上である
イ:RはSより4学年上である
ウ:TはUより1学年上である
このとき、Uは何年生の担任か。
【解答&解説】
左から6年生→1年生の順番で記載するものとします。
条件アより、P〇〇〇〇Qです。
条件イより、R〇〇〇〇Sです。
条件ウより、TUでワンセットです。
上記を組み合わせると、PR〇〇QSまたはRP〇〇SQです。
TUは〇〇にあてはまるので、Uは3年生・・・(答)の担任であることがわかります。
🔽 本にも載ってない極秘情報 🔽
今回はSPIの非言語で出題される1本のロープ問題を取り上げました。
図をしっかり書いて情報を整理していけば簡単に解けるので、ぜひ意識してみてください。


