
SPIの非言語(数学)の勉強・対策を限られた時間の中で効率よく行うためには、非言語の問題を解くために必要な公式をしっかりと頭に入れることが重要です。
※「SPIとは?対策方法や問題・例題をすべて紹介!適性検査SPIはこれで完璧だ!」もぜひ合わせてご覧ください。
しかし、SPIを受検予定の就活生や転職活動中の社会人の中にはSPIの非言語(数学)の問題を解くにあたってどの公式を覚えればよいかわからないという人も多いのではないでしょうか?
※「【SPI】転職・中途採用の対策法や問題・通過率などをSPIマスターが完全解説」もぜひ参考にしてください。
数学には覚えきれないほどの多くの公式が存在しますが、SPIで必要な公式はそこまで多くありません。
今回は今までにSPIを100回以上受検し、日本一SPIに詳しいSPIマスターの私カズマがSPIの非言語(数学)で本当に必要な公式43個を出題頻度別にご紹介します。
SPIの点数を短期間でアップさせたい人はぜひ最後までご覧ください。
※「SPIの対策方法・勉強法を日本一SPIに詳しい筆者が真剣に考えてみた」もぜひ合わせてご覧ください。
ちなみにですが、SPIにはたった3時間の勉強でSPIが通過してしまう勉強法があります。
これさえあれば限りなく少ない努力で内定に大きく近づきます。
これは私が100回以上ものSPI受検を通して生み出した、どの本にも載っていない超コスパの良い究極の勉強法です。
興味のある人はぜひ以下のボタンからその方法をチェックしてみてください。
目次
SPIの公式一覧(暗記必須)
まずはSPIの非言語の問題を解くためには絶対に必要となる公式(というより知識)をご紹介します。
以下の6つは必ず暗記・できるようにしておいてください。答えを求めるための計算の過程などでも使うので、理解していないと間違いなく壊滅的な点数になります。
※「SPIの非言語は0点・ボロボロ・壊滅的でも通過・内定する?受かった事例は?転職は?」もぜひ参考にしてください。
- 分数の表記と分数→小数への変換
- 四捨五入
- 一次方程式と連立方程式の解き方
- 増加率の計算
それぞれ順番に解説していきます。
分数の表記と分数→小数への変換
SPIでは例えば、10分の1は1/10、マイナス8分の3は-3/8のように記号「/」を使って表記されます。
この表記には必ず受検前に慣れておきましょう。
そして、SPIでは分数を小数に変換する場面も登場します。分数から小数への変換は「分子÷分母」の計算を行います。
例えば、1/10=1÷10=0.1、-6/25=(-6)÷25=-0.24となります。
※分数の計算方法についてはSPIの分数について詳しく解説した記事をご覧ください。
四捨五入
SPIでは「答えは小数点以下第3位を四捨五入せよ」のような指示が出る場合があります。
「小数点以下第3位を四捨五入せよ」は「小数点第3位を四捨五入せよ」という意味です。
「以下」という言葉が登場することで混乱してしまう人がいるのでご注意ください。
例えば、1.234という小数に対して「小数点以下第3位を四捨五入せよ」という指示が出た場合は小数点第3位である4を四捨五入して1.23となります。
一次方程式と連立方程式
SPIでは答えを求める過程の計算で一次方程式、連立方程式が登場する場合があります。
一次方程式とは、5x+3=6や0.6a-10=3などの方程式のことです。
連立方程式とは、
- a+b=40
- 5a+9b=26
などの方程式のことです。
本記事では詳しい計算方法は割愛します。計算方法を忘れてしまった人は【SPI】方程式はこの2つだけ絶対覚えよう!例題でわかりやすく解説!練習問題付きをご覧ください。
ちなみにですが、二次方程式や不定方程式など一次方程式と連立方程式以外の方程式は不要です。
増加率の計算
例えば、あるお菓子の料金が100円から150円に値上げされたとき、この料金の増加率(値上げ率)を自力で計算することはできますでしょうか?
増加率=(変化後の数値-変化前の数値)÷変化前の数値×100で計算できます。
なので、上記の増加率=(150-100)÷100×100=50[%]となります。
この計算方法も必ず覚えておいてください。
※増加率の計算についてもっと詳しく学習したい人は【SPI】増加率の計算式は暗記必須!忘れてしまったときの対処法もご紹介をご覧ください。
🔽 本にも載ってない極秘情報 🔽
SPIの公式一覧(出題頻度=高)
ここからはSPIの非言語(数学)で出題頻度が高い公式を練習問題と合わせてご紹介していきます。
公式の一覧は以下の通りです(一部用語やテクニックもあり)
- 割合と比の公式
- 速度算の公式
- 料金の割引に関する公式
- 損益算に関する用語
- 組み合わせCと順列Pの公式
- サイコロを2個使う問題で使えるテクニック
それぞれ順番に解説していきます。
※「SPIの非言語(数学)を完全解説!対策方法やできない人でも点数を上げる方法!問題もご紹介」もぜひ合わせてご覧ください。
割合と比の公式
割合と比では以下3つの公式を必ず覚えてください。
- %の変換方法(例:200の10%=200×10%=200×0.1=20)
- 「は」÷「の」の法則
- 内項の積=外項の積
※公式の詳細に関しては「【SPI】割合と比の練習問題20問!難しい?公式や解き方・コツもわかりやすく解説!」をご覧ください。
【練習問題】
グループAの男女比は2:3、グループBの男女比は5:7で、いずれも女性の方が多い。2つのグループの合計は96人でグループAの男性が24人のとき、グループBの男性の人数を求めよ。
【解答&解説】
グループAの女性の人数をa人とすると、2:3=24:aが成り立ちます。
上記でご紹介した公式「内項の積=外項の積」より、3×24=2aとなるので、a=36が求まります。
よってグループBの人数は96-(24+36)=36[人]となるので、グループBの男性の人数は36 × 5/(5+7)=15[人]・・・(答)となります。
速度算の公式
速度算では以下4つの公式を覚えてください。
- 距離と時間の換算(1km=1000m、1m=100cm、1時間=60分、1分=60秒、1時間=3600秒)
- 速度の換算(30m/分=1.8km/時、30m/分=0.5m/秒など)
- き・は・じの法則
- 平均速度=距離÷時間の合計
き・は・じの法則は以下のことです(小学校で学習する内容です)

平均速度は距離を時間で割ったものです。
例えば、120kmの道のりを行きは40km/時、帰りは60km/時で往復した場合、行きは120÷40=3[時間]、帰りは120÷60=2[時間]かかるので、平均速度は(120×2)÷(3+2)=48km/時となります。
※「【SPI】速度算の練習問題18問!コツや解き方・公式・計算方法を完全解説!」もぜひ参考にしてください。
【練習問題】
P地点からQ地点まで、行きは4km/時、帰りは6km/時で往復したところ、所要時間は2時間30分だった。P地点からQ地点までの距離は何kmか求めよ。
【解答&解説】
2時間30分は時間に変換すると2.5時間です。PからQまでの距離をa[km]とすると、上記の公式「時間=距離÷速さ」より、
a/4 + a/6 =2.5が成り立ちます。これを整理すると、
5/12 a =2.5となるので、a=2.5 × 12/5 =6[km]・・・(答)となります。
料金の割引に関する公式
例えば、200円の30%引きはいくらか?と聞かれたとき、皆様は瞬時に回答できますでしょうか?
答えは200×(1-0.3)=200×0.7=140[円]となります。
割引後の料金=料金×(1-割引率)となります。
ちなみにですが、割引額(200円-140円=60円)は200×0.3=60[円]で求めることができます。
つまり、割引額=料金×割引率となります。
料金の割引に関する問題はSPIで頻出なので、必ずできるようにしておきましょう。
※「【SPI】料金の割引に関する練習問題16選!必ず覚えるべき公式や解き方をわかりやすく解説」もぜひ合わせてご覧ください。
🔽 本にも載ってない極秘情報 🔽
損益算に関する用語
損益算とは何か商品やモノ・サービスを販売したときに、
- 〇〇円の利益を得るにはいくらで売ればいいか?
- 〇〇円で販売したときの利益または損失はいくらか?
などを考える計算のことです。
以下5つの用語が登場するので、必ず覚えてください。
- 原価
- 仕入れ値(原価と同じ意味)
- 定価
- 売値
- 利益
それぞれの用語の詳細に関しては「【SPI】損益算の練習問題20選!コツと公式もわかりやすく解説!捨てるのはあり?」をご覧ください。
【練習問題】
ある商品を定価の40%引きにして売ったら定価の800円引きになった。この商品の定価はいくらか求めよ。
【解答&解説】
定価をa[円]とおきます。その0.4倍が800円なので、0.4a=800より、a=2000[円]・・・(答)となります。
組み合わせCと順列Pの公式
組み合わせはとは、あるモノや人の中から何個・何人かを選び出す方法は何通りあるか?を計算することです。並べる順番は考慮しないのがポイントです。
組み合わせの公式ですが、異なるn個のものの中から異なるr個を取り出す組み合わせの総数はnCrで表すことができます。
nCrの計算方法は、例えば
- 4C2=(4×3)/(2×1)=6
- 8C3=(8×7×6)/(3×2×1)=56
- 10C4=(10×9×8×7)/(4×3×2×1)=210
となります。
それに対して順列は組み合わせと違い、並べる順番も考慮します。
順列の公式ですが、異なるn個のものの中から異なるr個を取り出し、順番も考慮して並べるときの場合の数はnPrで表すことができます。
nPrの計算方法ですが、例えば
- 5P2=5×4=20
- 6P3=6×5×4=120
- 7P4=7×6×5×4=840
となります。
組み合わせと順列について詳しく学習したい人はSPIの組み合わせの公式と順列との違いについて解説した記事をご覧ください。
【練習問題】
男子4人、女子5人のグループから男女各2人ずつの代表を選ぶとき、その選び方は何通りあるか求めよ。
【解答&解説】
男子4人から2人を選ぶ選び方は4C2=6[通り]で、女子5人から2人を選ぶ選び方は5C2=10[通り]です。
よって答えは6×10=60[通り]・・・(答)となります。
サイコロを2個使う問題
SPIではサイコロを2個投げるまたはサイコロを2回投げる場合の確率や場合の数に関する問題が出題される場合があります。
例えば、サイコロを2個投げた(2回投げた)ときのサイコロの目の和に関する問題を解くときは以下のような表があると非常に便利です。
| 和 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
サイコロを2個投げた(2回投げた)ときのサイコロの目の積や差に関する問題を解くときも、以上のような表の積バージョンや差バージョンを作れば簡単に問題が解けます。
※詳しくはSPIのサイコロ問題の解き方について解説した記事をご覧ください。
【練習問題】
大小2個のサイコロを振ったとき、出た目の和が3の倍数になる確率を求めよ。
【解答&解説】
上記のサイコロの表より、出た目の和が3の倍数になるパターンは12通りあることがわかります。
よって答えは12/36=1/3・・・(答)となります。
🔽 本にも載ってない極秘情報 🔽
SPIの公式一覧(出題頻度=中)
ここからはSPIの非言語(数学)で出題頻度が中くらいの公式をご紹介していきます。余力がある人は覚えておきましょう。
公式の一覧は以下の通りです。
- 平均世帯人数の公式(求め方)
- 通過算の公式
- 流水算の公式
- 確率の公式
では、順番に解説していきます。
平均世帯人数の公式(求め方)
SPIでは平均世帯人数を求める問題がたまに出題されます。求め方は難しくないので知っておきましょう。
平均世帯人数=世帯人数の合計÷世帯数となります。
例えば、以下のような3つの部屋があるアパートにそれぞれ1人・2人・3人が住んでいるとします。
| 部屋番号 | 101 | 102 | 103 |
|---|---|---|---|
| 住んでいる人の数 | 1人 | 2人 | 3人 |
このとき、世帯数=部屋の数なので3世帯となります。世帯人数の合計は1+2+3=6[人]となります。
よって、以上のアパートの平均世帯人数は6÷3=2[人]となります。
平均世帯人数に関してもっと詳しく学習したい人はSPIの平均世帯人数について解説した記事をご覧ください。

通過算の公式
通過算は電車や車が橋やトンネルを通ったりするときの速度や時間などを求める問題です。
通過算で必要な公式は以下の3つです。
- 電車がトンネルを通過するのにかかる時間=(電車の長さ+トンネルの長さ)÷(電車の速度)
- 電車が他の電車を追い越すときにかかる時間=(電車の長さの合計)÷(速度の差)
- 電車同士がすれ違うときにかかる時間=(電車の長さの合計)÷(速度の和)
【練習問題】
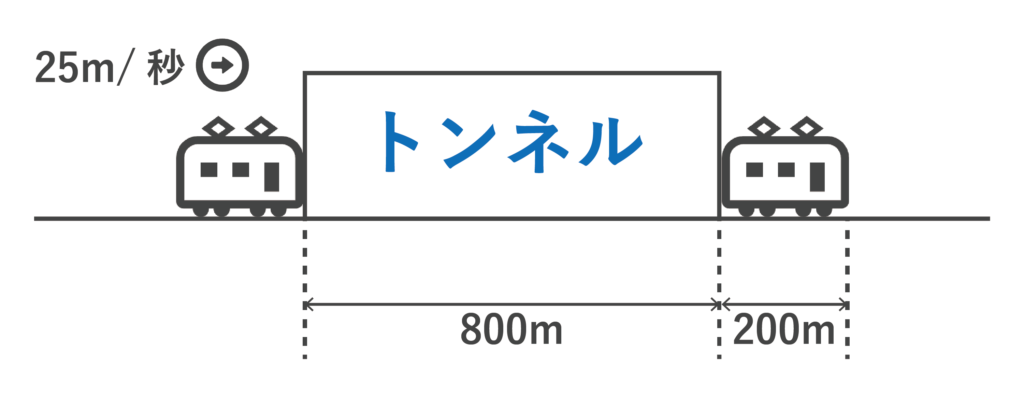
25m/秒で走行している長さ200mの電車が長さ800mのトンネルを通過するのにかかる時間は何秒か求めよ。
【解答&解説】
上記でご紹介した通過算の1つ目の公式より、(200+800)÷25=40[秒]・・・(答)となります。
※「通過算はSPIで出題されます!覚えておくべき3つのパターンとは?」もぜひ参考にしてください。
流水算の公式
流水算を解くにあたって知っておきたい公式は以下の5つです。
- 船が川を上るときの速さ=(静水時の船の速さ)+(川の流れの速さ)
- 船が川を下るときの速さ=(静水時の船の速さ)-(川の流れの速さ)
- 時間の逆比=速度の比
- 川の流れの速さ=(下りの船の速さ-上りの船の速さ)÷2
- 静水時の船の速さ=(上りの船の速さ+下りの船の速さ)÷2
例えば、静水時(=水の流れが全くない状況)の速度=a[km/時]である船が、速さb[km/時]で流れている川を下りることを想定してみましょう。
このとき、船の速度は川の流れの速さの分だけ加速されるので(a+b)km/時となります。
逆に、船が川を上るときは川の流れの速さの分だけ船の速度は遅くなります。
静水時の速度=a[km/時]である船が、速さb[km/時]で流れている川を上ることを想定した場合、船の速度は(a-b)km/時となります。
流水算について詳しく学びたい人はSPIの流水算の解き方について解説した記事をご覧ください。
【練習問題】
船が川を20km上るのに4時間、下るのに2時間かかった。このとき、船の速さは時速何kmか求めよ。
【解答&解説】
静水時の船の速度をa[km/時]、川の流れの速さをb[km/時]とおきます。
すると、速度算の公式より距離÷時間=速さなので
- 20÷4=a-b・・・①
- 20÷2=a+b・・・②
という連立方程式を立てることができます。
①+②より、15=2aとなるのでa=7.5[km/時]・・・(答)となります。
確率の公式
SPIの確率の問題を解くにあたっては、
- Pが発生する確率=(Pが発生する場合の数)/(すべての場合の数)
- 和事象
- 積事象
- 余事象
の4つを理解しておきましょう。
「AまたはBが起こる」という事象をAとBの和事象といいます。和事象は(Aが起こる確率)+(Bが起こる確率)で計算することができます。
「AとBが同時に起こる」という事象をAとBの積事象といいます。積事象は(Aが起こる確率)×(Bが起こる確率)で計算することができます。
そして、事象Pに対して、Pが起こらないという事象をPの余事象といい、少なくともPが起こる確率=1-(Pが起こらない確率)で求めることができます。
問題文に「少なくとも」という記載があれば余事象を疑いましょう。
※それぞれの詳細は「【SPI】確率の練習問題18問!難しい?出ないという噂は?公式は?」をご覧ください。
【練習問題】
4枚のコインを同時に投げるとき、少なくとも1枚が表になる確率を求めよ。
【解答&解説】
少なくとも1枚が表になる確率=1 – (4枚すべてが裏になる確率)で求めることができます。
よって、答えは1 – (1/2)4=15/16・・・(答)となります。
SPIの公式一覧(出題頻度=低)
SPIで使用する可能性が低いですが、念のため覚えておくと便利な公式は以下の2つです。
- 濃度算の公式
- ジャンケンであいこになる確率
順番に解説していきます。
濃度算の公式
a[%]の食塩水b[グラム]に含まれる食塩の量はb × a%=(b × a/100)グラムとなります。
例えば、10%の食塩水200グラムに含まれる食塩の量は200×10%=200 × 10/100=20[グラム]となります。
また、食塩水の濃度[%]は、食塩水に含まれる食塩の量 / 食塩水の重さ ×100で求めることができます。
SPIで濃度算が出題される可能性は極めて低いですが、そこまで難しい公式ではないので知っておきましょう。
※詳しくは「SPIで濃度算は出る?公式は?SPIを100回以上受検した筆者が体験談をもとに解説」をご覧ください。
【練習問題】
濃度3%の食塩水150gに水を100g加えると、食塩水の濃度は何%になるか。
【解答&解説】
濃度3%の食塩水150gに含まれる食塩の量は150×0.03=4.5[g]です。
よって、答えは4.5 ÷ (150+100)×100=1.8[%]・・・(答)となります。
ジャンケンであいこになる確率
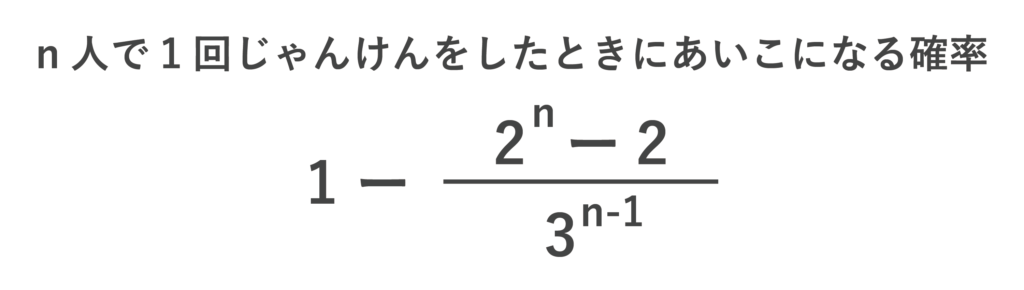
n人で1回じゃんけんをしたときにあいこになる確率は1 – (2n-2)/3n-1 となります。
※証明は複雑なので割愛します。
例えば、3人で1回じゃんけんをしたときにあいこになる確率は
1 – (23-2)/3(3-1)=1 – (8-2)/9 =1 – 6/9=1/3 となります。
知っているとかなり便利な公式なので余力がある人は覚えておきましょう。
🔽 本にも載ってない極秘情報 🔽
いかがでしたでしょうか?
今回はSPIの非言語(数学)で必要な公式をご紹介していきました。
数学にはたくさんの公式が存在しますが、SPIで必要な公式は上記の通りそこまで多くはありません。
SPIで高得点を狙っている人は本記事でご紹介した公式はすべて覚えておきたいところです。


