SPIのWEBテスティングの能力検査では言語と非言語の2科目が用意されています。
WEBテスティングの非言語は難しいと感じる人が多いので、必ず勉強・対策をしておきましょう。
※詳しくは「WEBテスティングの非言語は難しい？100人に調査してみた」をご覧ください。
今では本屋に行けばSPIの対策本がたくさん販売されていますが、ほとんどはテストセンター対策のための対策本であり、WEBテスティングで出題される問題はあまり掲載されていません。
※おすすめのWEBテスティングの問題集をランキング形式でご紹介した記事もぜひ参考にしてください。
そこで今回はSPIを過去100回以上も受検し、日本一SPIに詳しい自信のある私カズマがWEBテスティングの非言語（数学）で出題される問題（例題）をご紹介していきます。
WEBテスティングを受検予定の就活生や転職活動中の社会人はぜひ参考にしてください。
ちなみにですが、たった3時間の勉強でWEBテスティングが通過してしまう勉強法があります。
これさえあれば限りなく少ない努力で内定に大きく近づきます。
これは私が100回以上ものSPI受検を通して生み出した、どの本にも載っていない超コスパの良い究極の勉強法です。
興味のある人はぜひ以下のボタンからその方法をチェックしてみてください。
WEBテスティングの非言語の例題まとめ
では早速、WEBテスティングの非言語の例題を一挙ご紹介していきます。
※WEBテスティングの非言語の出題範囲については「WEBテスティングの練習問題・出題範囲まとめ！本番のSPIに近い難易度です！」に記載しているので、ぜひ参考にしてください。
また、SPIでは非言語の問題を解くにあたって必ず覚えておかなくてはならない数学の公式があります。
数学に自信がない人は以下の問題を解く前にSPIの公式一覧（非言語・数学）をまとめた記事を読むことをおすすめします。
損益算
【例題】
ある商品に4割の利益を見込んで定価をつけたが、売れなかったので定価の2割引にしたところ36円の利益が出た。この商品の原価はいくらか求めよ。
【解答＆解説】
原価をa円とおきます。
すると、1.4a×0.8-a＝36という方程式が立てられるので、これを整理して
1.12a-a＝36より0.12a＝36となるので、a＝36÷0.12＝300[円]・・・（答）となります。
※原価や定価などの用語の意味がわからない人は「SPIの損益算とは？コツと暗記必須の用語4つをわかりやすく解説！」をご覧ください。
流水算
【例題】
川に沿って60km離れた2地点を船で往復したところ、上りは6時間、下りは4時間かかった。この船の静水時の速度は時速何kmか求めよ。
【解答＆解説】
上りの速さは60÷6＝10[km/時]、下りの速さは60÷4＝15[km/時]となりますね。
静水時の船の速度は上りの速さと下りの速さの平均になるので、求める答えは（10＋15）÷2＝12.5[km/時]・・・（答）となります。
※「SPIの流水算の解き方！公式や比を使った手法も例題でわかりやすく解説！」もぜひ参考にしてください。
速度算
【例題】
Aさんが家を出発して300m進んだとき、Bさんが90m/分の速さでAさんを追いかけたところ、Bさんが家を出発してから6分後にAさんに追いついた。Aさんの速さは分速何mか求めよ。
【解答＆解説】
速さ＝距離÷時間です。AさんとBさんの速さの差は300÷6＝50[m/分]であることがわかります。
AさんはBさんより遅いので、Aさんの速さは90-50＝40[m/分]・・・（答）となります。
※「SPIの速度算・速さの計算の解き方とコツ！重要公式もご紹介」もぜひ参考にしてください。
仕事算
【例題】
Pさんがすると3時間、Qさんがすると6時間かかる仕事がある。この仕事を2人ですると何時間で終わるか求めよ。
【解答＆解説】
仕事の量を3と6の最小公倍数である6とおいてみます。
するとPさんは1時間で6÷3＝2の仕事をこなすことが可能であるとわかります。
同様に考えてQさんは1時間で6÷6＝1の仕事をこなすことが可能です。
2人で一緒に仕事をすると、1時間で2＋1＝3の仕事をこなすことができます。
仕事の量は6なので、答えは6÷3＝2[時間]・・・（答）となります。
※「仕事算はSPIの出題範囲！解き方や2人・3人のケース・最小公倍数を使った手法もわかりやすく解説！」もぜひ参考にしてください。
🔽 本にも載ってない極秘情報 🔽
割合と比
【例題】
ある会社の社員のうち、女性社員の割合は全体の25%を占めていたが、女性社員が2人増員されたので30%となった。増員前の社員数は何人か求めよ。
【解答＆解説】
増員前の会社の社員数をa人とすると、0.25a＝0.3（a＋2）-2という方程式が立てられるので、
0.05a＝1.4より、a＝1.4÷0.05＝28[人]・・・（答）となります。
※「SPIの割合と比の解き方とコツ！暗記必須の公式とは？練習問題付き」もぜひ参考にしてください。
代金精算
【例題】
P、Q、Rの3人で旅行に行き、Pは3人分の宿泊費21000円、Qは食事代18000円、Rは交通費30000円を支払った。3人の支払額が均等になるようにするにはPはRにいくら支払えば良いか求めよ。
【解答＆解説】
1人あたりの負担額は（21000＋18000＋30000）÷3＝23000[円]であることがわかります。
よってPはRに23000-21000＝2000[円]・・・（答）支払えば良いことがわかります。
※「SPIの代金精算の解き方・コツを例題でわかりやすく解説！難しい・苦手と感じる人必見！」もぜひ合わせてご覧ください。
年齢算
【例題】
現在、父は34歳、娘は6歳である。父の年齢が娘の年齢の8倍だったのは今から何年前か。
【解答＆解説】
a年前に父の年齢が娘の年齢の8倍だったとします。
すると、34-a＝8（6-a）という方程式ができるので、34-a＝48-8aより、7a＝14となるので、a＝2[年前]・・・（答）となります。
料金割引
【例題】
水族館の入館料は1人あたり1000円である。30人を超える団体の場合、31人目から入館料が3割引になる。ある団体がこの水族館に入館したとき、入館料の1人あたりの平均は900円だった。この団体の人数を求めよ。
【解答＆解説】
入館料の1人あたりの平均が900円であり、1000円を下回っているので、この団体は30人を超える団体であることがわかります。
団体の人数をa人とおくと、1000×30＋（a-30）×1000×0.7＝900aという方程式が立てられるので、
30000＋700a-21000＝900aより、200a＝9000となるので、a＝45[人]・・・（答）となります。
※「料金の割引はSPIの出題範囲！必ず覚えるべき公式もわかりやすく解説！練習問題付き」もぜひ参考にしてください。
鶴亀算
【例題】
1個200円のクッキーと1個150円のチョコを合わせて20個買ったところ、代金は3600円だった。このとき、チョコは何個買ったか求めよ。
【解答＆解説】
購入したクッキーの数をa個、チョコの数をb個とおくと、
- a＋b＝20・・・（1）
- 200a＋150b＝3600・・・（2）
という連立方程式を立てることができます。
（1）×200-（2）より、50b＝20×200-3600＝400となるので、b＝400÷50＝8[個]・・・（答）となります。
※「SPIの鶴亀算の解き方・コツを例題でわかりやすく解説！練習問題付き」もぜひ参考にしてください。
整数問題
【例題】
A、B、Cの3人がサイコロを1回ずつ振った。出た目について以下のことがわかっている。
ア：AとBの目の和はCの3倍だった
イ：数が大きい順にA、B、Cだった
このとき、Aが出した目の数を求めよ。
【解答＆解説】
イより、A＞B＞Cであり、Cは3人の中で最小の数であり、同じ数の人はいないことからCは4以下であることがわかります。
Cの目の数で場合分けをしてAとBを検討していきます。
＜C＝1のとき＞
A＋B＝3となりますが、A＞B＞Cを満たすA、Bは存在しません。
＜C＝2のとき＞
A＋B＝6となりますが、A＞B＞Cを満たすA、Bは存在しません。
＜C＝3のとき＞
A＋B＝9となり、A＝5、B＝4であれば条件を満たします。
＜C＝4のとき＞
A＋B＝12となりますが、A＞B＞Cを満たすA、Bは存在しません。
よって答えはA＝5・・・（答）となります。
※「SPIの整数問題10選！難易度が高いので要注意」もぜひ参考にしてください。
推論
【例題】
以下について、ア・イの情報のうち、どれがあれば[問]の答えがわかるかを考え、選択肢1〜5の中から正しいものを1つ選び、答えなさい。
ミカン、リンゴ、モモがそれぞれ1個ずつ以上あり、合計は20個である。
[問]ミカンは何個あるか
ア：リンゴはミカンより多い
イ：リンゴとモモは合わせて13個ある
- アだけでわかるが、イだけではわからない
- イだけでわかるが、アだけではわからない
- アとイの両方でわかるが、片方だけではわからない
- アだけでも、イだけでもわかる
- アとイの両方があってもわからない
【解答＆解説】
まずはアから見ていきます。リンゴ＞ミカンという条件だけではミカンが何個あるかを特定することはできません。
続いてイですが、リンゴ＋モモ＝13より、ミカン＝20-13＝7[個]となり、ミカンの数を特定することができます。
よって答えは2・・・（答）となります。
※「SPIの推論とは？すべてがわかる！時間足りない・苦手な人向けの対策方法も解説」もぜひ参考にしてください。
集合・ベン図
【例題】
50人にアンケートを取ったところ、映画が好きな人は28人、音楽が好きな人は25人、どちらも好きではない人は12人いた。このとき、映画も音楽も好きな人は何人いるか求めよ。
【解答＆解説】
映画も音楽も好きな人をa人とおきます。
問題文の条件をベン図にすると以下のようになります。
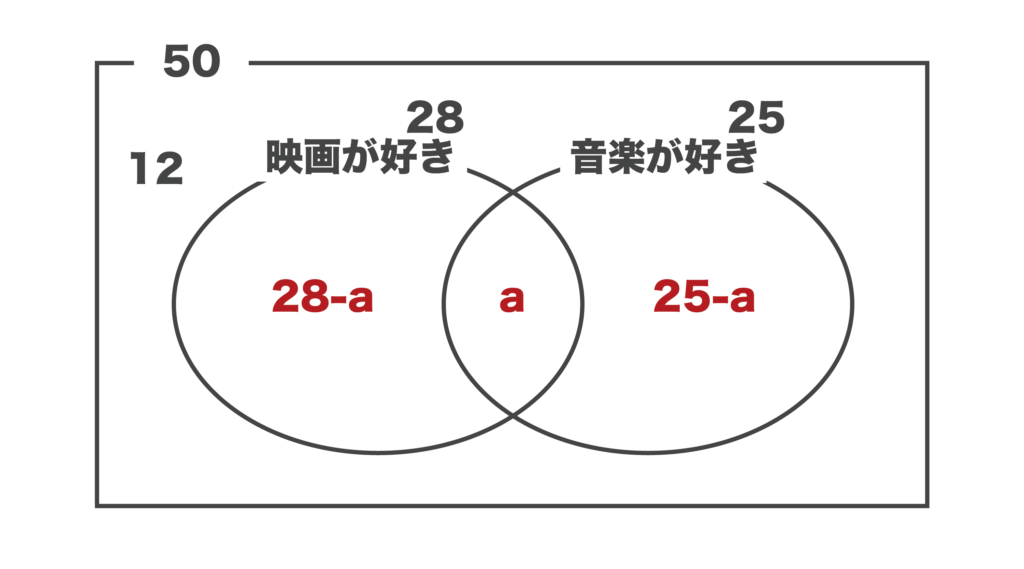
上記のベン図より、12＋（28-a）＋a＋（25-a）＝50という方程式を立てることができます。
これを整理すると、65-a＝50となるので、a＝15[人]・・・（答）となります。
※「SPIの集合・ベン図の解き方を例題でわかりやすく解説！コツと練習問題も」もぜひ参考にしてください。
図表の読み取り
【例題】
以下の表はある飲食店の4つの店舗P、Q、R、Sにおける肉・魚・野菜のある週の合計仕入れ量とその割合を示したものである。
| P | Q | R | S | |
|---|---|---|---|---|
| 合計仕入れ量 | 92kg | 110kg | 103kg | 76kg |
| 肉 | 68% | 64% | 40% | 25% |
| 魚 | 14% | 10% | 28% | 35% |
| 野菜 | 18% | 26% | 32% | 40% |
| 合計 | 100.0% | 100.0% | 100.0% | 100.0% |
（1）肉より魚の仕入れ量が多かった店舗では、魚は肉の何倍仕入れられているか求めよ。必要なときは最後に小数点以下第2位を四捨五入すること。
（2）各店舗の肉の仕入れ量を大きい順に並べたとき、その順番として正しいものは以下1〜6のうちどれか。1つ選びなさい。
- P、Q、R、S
- Q、P、R、S
- P、Q、S、R
- R、P、Q、S
- R、Q、P、S
- S、P、Q、R
【解答＆解説】
（1）表より、肉より魚の仕入れ量が多かった店舗はSであることがわかります。
よって答えは35÷25＝1.4[倍]・・・（答）となります。
※四捨五入を行う必要はありませんでした。
（2）各店舗の肉の仕入れ量を求めていきます。
- P：92×0.68＝62.56[kg]
- Q：110×0.64＝70.4[kg]
- R：103×0.4＝41.2[kg]
- S：76×0.25＝19[kg]
よって大きい順に並べるとQ・P・R・Sとなるので、答えは2・・・（答）です。
※「SPIの図表の読み取りは対策必須！必ず覚えておくべき知識をご紹介します」もぜひ合わせてご覧ください。
場合の数
【例題】
1、2、3、4、5の5枚のカードを順に取り出すときに出る数の並べ方のうち、2枚目と4枚目に偶数が出る並べ方は何通りあるか求めよ。
【解答＆解説】
2枚目と4枚目には2か4が入るので、ここでの並べ方は2×1＝2[通り]です。
1枚目、3枚目、5枚目には1、3、5が入るので、3×2×1＝6[通り]です。
よって答えは2×6＝12[通り]・・・（答）となります。
※「SPIで場合の数は頻出！解き方のコツと出題パターンを完全網羅！練習問題付き」もぜひ参考にしてください。
確率
【例題】
当たりが1つだけある6個のくじがある。このくじを6人で引くとき、3人目が当たりを引く確率を求めよ。ただし、引いたくじは戻さないものとする。
【解答＆解説】
引いたくじは戻さないので、全体のくじの数は1個ずつ減ります。
1人目がハズレの確率は5/6、2人目がハズレの確率は4/5、3人目が当たる確率は1/4です。
よって答えは5/6 × 4/5 × 1/4 ＝1/6・・・（答）となります。
※「SPIの確率の解き方を例題で解説！難しい？出ないという噂は？練習問題付き」もぜひ参考にしてください。
WEBテスティングの出題範囲となっている非言語の例題は以上となります。
ちなみにですが、たった3時間の勉強でWEBテスティングが通過してしまう勉強法があります。
これさえあれば限りなく少ない努力で内定に大きく近づきます。
これは私が100回以上ものSPI受検を通して生み出した、どの本にも載っていない超コスパの良い究極の勉強法です。
興味のある人はぜひ以下のボタンからその方法をチェックしてみてください。
