
SPIにはWEBテスティングといわれる受験方式があります。
WEBテスティングは自分のPCから受検期限内であれば好きな場所・時間にSPIが受検できるのが特徴です。
※詳しくは「SPIのWEBテスティングとは?完全解説!本にも掲載されていない極秘裏ワザもご紹介」をご覧ください。
今回はWEBテスティングを受検予定の就活生・転職活動中の社会人のために、本番のSPI(WEBテスティング)で出題される問題の難易度に近い問題を分野ごとにまとめました。
解答&解説も付けているので、ぜひ解いてみてください。
ちなみにですが、たった3時間の勉強でWEBテスティングが通過してしまう勉強法があります。
これさえあれば限りなく少ない努力で内定に大きく近づきます。
これは私が100回以上ものSPI受検を通して生み出した、どの本にも載っていない超コスパの良い究極の勉強法です。
興味のある人はぜひ以下のボタンからその方法をチェックしてみてください。
WEBテスティングの問題(非言語)
WEbテスティングの能力検査では言語と非言語の2科目が用意されています。
言語=国語、非言語=数学のことです。
英語と構造把握は出題されないのでご注意ください。
※「SPIの英語はこれで完璧!出題される形式や問題・対策方法などを一挙ご紹介」もぜひ参考にしてください。
まずはWEBテスティングの非言語で出題される問題からご紹介していきます。
※本サイトではWEBテスティングの模擬試験をご用意しています。興味のある人は「【SPI-G】WEBテスティングの模擬試験(テスト)!本番に近い難易度です」をご覧ください。
割合と比
【問題】
グループAの男女比は2:3、グループBの男女比は5:7で、いずれも男性の方が少ない。2つのグループの合計は96人である。Aグループの男性が24人であるとき、グループBの女性の人数を求めよ。
【解答&解説】
Aグループの男性が24人という情報から、24:(グループAの女性)=2:3より、グループAの女性=24 × 3/2 =36[人]であることがわかります。
したがって、グループBの人数=96-(24+36)=36[人]となります。
グループBの男女比は5:7とのことなので、グループBの女性の人数=36 × 7/12 =21[人]・・・(答)となります。
※「SPIの割合と比の解き方とコツ!暗記必須の公式とは?練習問題付き」もぜひ参考にしてください。
方程式
【問題】
2つの自然数AとBがあり、Aの1/3はBの1/5である。また、AとBの差は18だった。このとき、Aの値を求めよ。
【解答&解説】
問題文より、1/3 × A=1/5 × Bとなります。
これを整理すると、5A=3Bとなるので、B=5/3 A であることがわかります。
よって、B>Aであることがわかるので、B-A=18となります。
B=5/3 A を B-A=18に代入すると、2/3 A=18となるので、A=18 × 3/2=27・・・(答)となります。
※「【SPI】方程式はこの2つだけ絶対覚えよう!例題でわかりやすく解説!練習問題付き」もぜひ参考にしてください。
整数問題
【問題】
10で割ると4余り、7で割ると6余る自然数のうち、最も小さい数を求めよ。
【解答&解説】
10で割ると4余る自然数は「10の倍数+4」となるので一の位が4の自然数(14、24、34、44・・・)となります。
7で割ると6余る自然数は1を足すと7で割り切れる自然数となります。
以上2つの条件を合わせると「7の倍数-1」のうち、一の位が4である自然数を求めれば良いことがわかります。
よって、まずは一の位が5である7の倍数を考えてみます。
一の位が5である最小の7の倍数は35なので、答えは35-1=34・・・(答)となります。
年齢算
【問題】
現在AはBよりも15歳若い。10年後には2人の年齢の合計は65歳になる。このとき、現在のAの年齢を求めよ。
【解答&解説】
現在のAの年齢をa歳とおいてみます。
すると、Bの年齢は(a+15)歳となりますね。
10年後には2人の年齢の合計が65歳なるとのことなので、
(a+10)+(a+15+10)=65という方程式が立てられます。
2a+35=65より、2a=30となるので、a=15[歳]・・・(答)となります。
※「SPIの年齢算は頻出なので対策必須!必ず知っておきたい解き方のコツとは?」もぜひ参考にしてください。
🔽 本にも載ってない極秘情報 🔽
速度算
【問題】
ある電車がP駅からQ駅を通過してR駅まで走行した。PQ駅間は平均時速78kmで12分、QR駅間は平均時速66kmで6分かかった。このとき、PR駅間の平均時速を求めよ。ただし、必要があれば最後に小数点以下第1位を四捨五入すること。
【解答&解説】
まずは単位を揃えて考えましょう。
速さの単位(km/時)に合わせて単位を揃えると、P駅からQ駅までに要した時間は12/60=0.2[時間]であることがわかります。
よってPQ駅間の距離=78×0.2=15.6[km]となります。
同様に考えて、Q駅からR駅までに要した時間=6/60=0.1[時間]なので、QR駅間の距離=66×0.1=6.6[km]です。
よって求める答えは(15.6+6.6)/(0.2+0.1)=22.2/0.3=74[km/時]・・・(答)となります。
※「SPIの速度算・速さの計算の解き方とコツ!重要公式もご紹介」もぜひ合わせてご覧ください。
損益算
【問題】
あるお店では仕入れ値に対して40%の利益を見込んで定価をつける。商品の値引きをして3000円で販売したところ、利益は仕入れ値の20%になった。このときの定価はいくらか求めよ。
【解答&解説】
仕入れ値をa円とおいてみます。すると、3000円で販売したときの利益は0.2a[円]と表すことができますね。
販売価格と仕入れ値の差が利益となるので、
3000 – a=0.2aより、1.2a=3000となるのでa=2500が求まります。
定価は仕入れに対して40%の利益を見込むので、定価は2500×1.4=3500[円]・・・(答)となります。
※「SPIの損益算とは?コツと暗記必須の用語4つをわかりやすく解説!」もぜひ参考にしてください。
料金割引
【問題】
ある植物園の入場料は1人あたり400円である。20人を超える団体は、20人を超える分について1人350円になる。30人で入場する場合、入場料の総額はいくらになるか求めよ。
【解答&解説】
20人までの総額は400×20=8000[円]です。
20人を超える分、つまり30-20=10[人]に関しては1人350円なので、その総額は350×10=3500[円]です。
よって求める答えは8000+3500=11500[円]・・・(答)となります。
※「料金の割引はSPIの出題範囲!必ず覚えるべき公式もわかりやすく解説!練習問題付き」もぜひ合わせてご覧ください。
代金精算
【問題】
P、Q、Rの3人がレストランで食事をしてQが11000円を支払った。3人は続けて2件目のバーに行き、その代金7900円はRが支払った。3人が同額ずつ負担する場合、PはQにいくら払えば良いか求めよ。
【解答&解説】
レストランとバーで支払った金額の合計は11000+7900=18900[円]ですね。
これを3人で割り勘にすると、1人あたりの負担額は18900÷3=6300[円]となります。
PはQに対して、1人あたりの負担額との差を支払えば良いので、Qに支払う金額=11000-6300=4700[円]・・・(答)となります。
ちなみにですが、PがRに支払う金額=7900-6300=1600[円]です。
※「SPIの代金精算の解き方・コツを例題でわかりやすく解説!難しい・苦手と感じる人必見!」もぜひ参考にしてください。
🔽 本にも載ってない極秘情報 🔽
図表の読み取り
【問題】
以下の表は航空輸送に関して年度ごとの旅客数と貨物重量を国内定期・国際の種別に表したものである。このとき、以下の問に答えよ。
| 国内定期の旅客数(千人) | 国内定期の貨物重量(万トン) | 国際の旅客数(千人) | 国際の貨物重量(万トン) | |
|---|---|---|---|---|
| 2021年 | 102,119 | 90.4 | 22,387 | 176.3 |
| 2022年 | 103,903 | 82.3 | 23,396 | 144.7 |
| 2023年 | 101,873 | 78.1 | 21,434 | 145.9 |
(1)国内定期と国際の合計旅客数に対して国際旅客数の割合が最も小さい年度について、その割合は何%か求めよ。ただし、必要なときは最後に小数点以下第2位を四捨五入すること。
(2)以下のア・イ・ウのうち正しいものはどれか。選択肢1〜6の中から1つ選びなさい。
ア:旅客数の減少率が最も大きいのは2023年度の国際である。
イ:2021年度と比較して2023年度の国内定期の貨物重量は10%以上減少した。
ウ:3年間の国際貨物重量の平均は153.3万トンである。
- アだけ
- イだけ
- ウだけ
- アとイの両方
- アとウの両方
- イとウの両方
【解答&解説】
(1)国内定期と国際の合計旅客数ですが、
- 2021年:102,119+22,387=124,506
- 2022年:103,903+23,396=127,299
- 2023年:101,873+21,434=123,307
です。よって、国際旅客数の割合は
- 2021年:22,387÷124,506×100≒17.98[%]
- 2022年:23,396÷127,299×100≒18.37[%]
- 2023年:21,434÷123,307×100≒17.38[%]
となります。最も割合が小さいのは2023年で17.38%なので、小数点以下第2位を四捨五入して答えは17.3[%]・・・(答)となります。
(2)まずはアから見ていきます。
旅客数が減少しているのは2022年から2023年にかけてのみです。
国内定期の旅客数の減少率は(101,873-103,903)÷103,903 ×100≒-15.5[%]です。
※増加率・減少率の計算方法がわからない人は「【SPI】増加率の計算式は暗記必須!忘れてしまったときの対処法もご紹介」をご覧ください。
国際の旅客数の減少率は(21,434-23,396)÷23,396 ×100≒-8.4[%]です。
よって、国内定期の旅客数の減少率の方が国際の旅客数の減少率よりも大きいので、アは間違いであることがわかります。
続いてイですが、
- 2021年度の国内定期の貨物重量=90.4
- 2023年度の国内定期の貨物重量=78.1
なので、その減少率は(78.1-90.4)÷90.4×100≒13.6[%]なので、イは正しいことがわかります。
最後のウですが、3年間の国際貨物重量の平均=(176.3+144.7+145.9)÷3≒155.6なので、ウは間違いであることがわかります。
以上より、イのみが正しいので答えは2・・・(答)となります。
※「SPIの図表の読み取りは対策必須!必ず覚えておくべき知識をご紹介します」もぜひ参考にしてください。
推論
【問題】
以下について、ア・イの情報のうち、どれがあれば[問]の答えがわかるかを考え、選択肢1〜5の中から正しいものを1つ選び、答えなさい。
A・B・Cの3人で回転寿司に行った。3人の食べた皿の合計は40皿だった。ただし、1人1皿は必ず食べるものとする。
[問]Aは何皿食べたか。
ア:AはBより4皿多かった。
イ:Cが食べた量は一番少なかった。
- アだけでわかるが、イだけではわからない
- イだけでわかるが、アだけではわからない
- アとイの両方でわかるが、片方だけではわからない
- アだけでも、イだけでもわかる
- アとイの両方があってもわからない
【解答&解説】
まずアから見ていきます。
「AはBより4皿多かった」という情報だけだと、
A=5皿、B=1皿、C=34皿やA=10皿、B=6皿、C=24皿などいくつかのパターンが考えられます。
なので、この情報だけではそれぞれが何皿食べたかを特定することはできません。
続いてイですが、こちらも「Cが食べた量は一番少なかった」という情報だけだと、
A=10皿、B=29皿、C=1皿やA=15皿、B=20皿、C=5皿などいくつかのパターンが考えられるので、この情報だけではそれぞれが何皿食べたかを特定することはできません。
では、アとイの2つの情報が揃っている場合はどうでしょうか?
こちらもA=19皿、B=15皿、C=6皿やA=21皿、B=17皿、C=2皿などいくつかのパターンが考えられてしまいます。
よって答えは5・・・(答)となります。
※「WEBテスティングで推論は出ない?出るので必ず対策しましょう!」もぜひ参考にしてください。
場合の数
【問題】
美術部には7人の部員がいる。この7人の中から部長と副部長を1人ずつ選ぶとき、選び方は全部で何通りあるか求めよ。
【解答&解説】
7人から部長を選ぶ選び方は7通りです。
残った6人の中から副部長を選ぶ選び方は6通りです。
よって求める答えは7×6=42[通り]・・・(答)となります。
※「SPIで場合の数は頻出!解き方のコツと出題パターンを完全網羅!練習問題付き」もぜひ合わせてご覧ください。
確率
【問題】
1から5までの数字が1つずつ書かれたカードが5枚ある。これらのカードをよく切って1枚ずつ順に並べ、5桁の数字を作った。このとき、百の位が1、一の位が2になる確率を求めよ。
【解答&解説】
5桁の数の並べ方は5×4×3×2×1=120[通り]です。
このうち、百の位が1、一の位が2に決まっているので、残り3つの数の並べ方は3×2×1=6[通り]になります。
よって求める確率は6/120=1/20・・・(答)となります。
※「SPIの確率の解き方を例題で解説!難しい?出ないという噂は?練習問題付き」もぜひ参考にしてください。
集合・ベン図
【問題】
高校生200人を対象にアンケートを取ったところ、サッカーが好きな人は140人、野球が好きな人は115人、どちらも好きではない人は50人いた。このとき、サッカーと野球の両方が好きな人は何人いるか求めよ。
【解答&解説】
まずは与えられた条件を以下のようにベン図にしてみます。
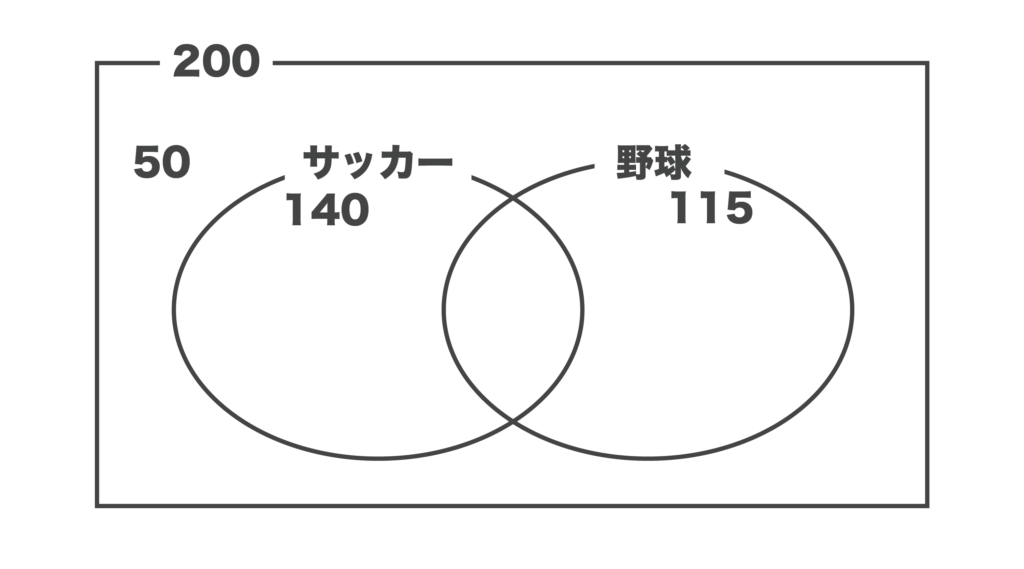
今回はサッカーと野球の両方が好きな人=a人とおいてみます。すると、以下のようなベン図が作れます。
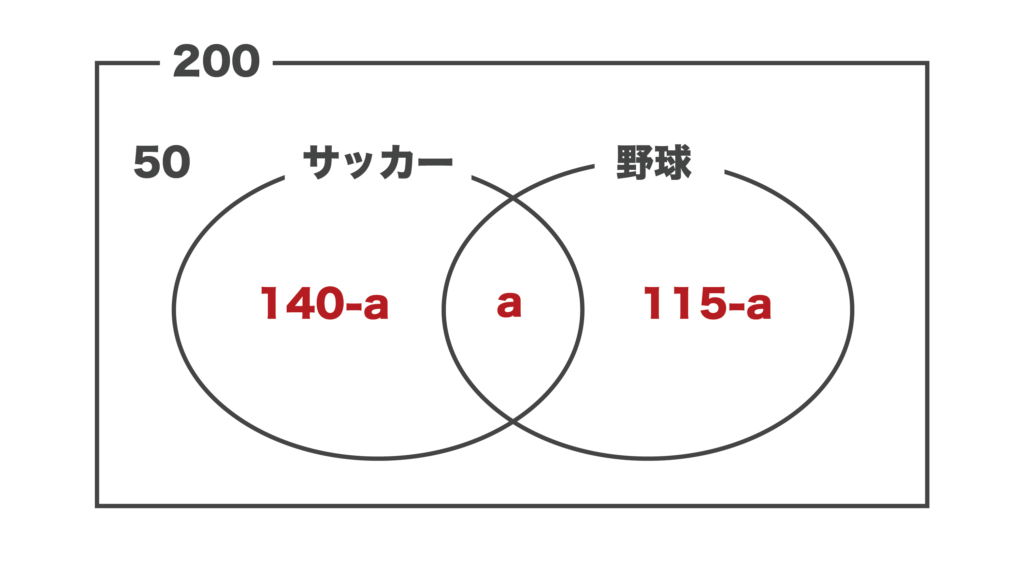
以上のベン図より、50+(140-a)+a+(115-a)=200という方程式が立てられます。
これを整理すると、305-a=200より、a=105[人]・・・(答)となります。
※「SPIの集合・ベン図の解き方を例題でわかりやすく解説!コツと練習問題も」もぜひ合わせてご覧ください。
非言語(数学)の問題は以上となります。
WEBテスティングに限らずですが、SPIの非言語(数学)は非常に幅広い分野から問題が出題されます。
すべての問題の対策をするのはなかなか難しい人もいるでしょう。
※「WEBテスティングの非言語は難しい?100人に調査してみた」もぜひ参考にしてください。
ちなみにですが、たった3時間の勉強でWEBテスティングが通過してしまう勉強法があります。
これさえあれば限りなく少ない努力で内定に大きく近づきます。
これは私が100回以上ものSPI受検を通して生み出した、どの本にも載っていない超コスパの良い究極の勉強法です。
興味のある人はぜひ以下のボタンからその方法をチェックしてみてください。
WEBテスティングの問題(言語)
ここからはWEBテスティングの言語で出題される問題をご紹介していきます。
※SPIの言語対策・頻出分野・練習問題などを完全解説した記事もぜひ参考にしてください。
言語では以下の分野の流れで問題が順番に出題されていきます。
※「WEBテスティングの言語を例題で徹底解説!点数アップの方法や出題範囲も」という記事もぜひ参考にしてください。
熟語の成り立ち
【問題】
以下の熟語の成り立ち方として適したものを選択肢1〜4の中から1つ選びなさい。
(1)最高
(2)読書
(3)頭痛
- 主語と述語の関係にある
- 動詞の後に目的語をおく
- 似た意味をもつ漢字を重ねる
- 1〜3のどれにもあてはまらない
【解答&解説】
(1)最高は「最も高い」と読むことができ、前の漢字が後の漢字を修飾していることがわかります。よって答えは4・・・(答)となります。
(2)読書は「書を読む」と読むことができるので、答えは2・・・(答)です。
(3)頭痛は「頭が痛い」と読むことができるので、答えは1・・・(答)です。
※「SPIの熟語の成り立ちとは?例題で解説&必ず覚えておくべきことをご紹介」もぜひ参考にしてください。
3文完成
【問題】
以下3つの文を完成させるために、A〜Eの中から最もつながりのよいものを1つずつ選びなさい。ただし、同じ選択肢を重複して使うことはできないものとする。
- 【 】、この程度の混雑などたいしたことはなかった。
- 【 】、電車が公共の空間であるという意識を持っていないのであろう。
- 【 】、急いでいる人からするとかなり迷惑である。
A:日本の満員電車に比べれば
B:電車が公共性を有している事実は
C:ドア付近で立ち止まっている人の存在は
D:車内ではしゃいだり、スマホで電話をしたりしている人は
E:プライベートを優先する人が増え
【答え】
1=A、2=D、3=C
文章の並び替え
【問題】
以下のア〜エに選択肢1〜4の語句を入れて文章を完成させるとき、ア〜エには何が入るかそれぞれ答えなさい。
ストレッチを毎日行うと【ア】【イ】【ウ】【エ】脂肪燃焼効果も高まると言われている。
- 体の代謝も上がるので
- 様々な動きに対応できるようになり
- 体の柔軟性が高まることで
- その後に行うエクササイズの
【答え】
ア=3、イ=2、ウ=1、エ=4
※「SPIの文の並び替え問題を解くコツは?練習問題もご用意しました」もぜひ参考にしてください。
🔽 本にも載ってない極秘情報 🔽
空欄補充
【問題】
以下の文中のア〜ウに入れるのに最適な語を1〜3の中から1つずつ選びなさい。ただし、それぞれの語は1回しか使えないものとする。
第五次男女共同参画基本計画では、若い世代の【ア】を積極的に取り入れることに重きをおいた。素案に対する意見公募では約5,600件が集まり、若い女性たちの切実な声が目立った。これを受け、就活中の学生へのセクハラ防止について【イ】を手厚くした。また、望まない妊娠を防ぐための「緊急避妊薬」についても処方箋なしに購入できるよう【ウ】するとした。
- 検討
- 要望
- 記述
【答え】
ア=2、イ=3、ウ=1
※「SPIの空欄補充問題は受検方式で毛色が違う!例題でわかりやすく解説」もぜひ合わせてご覧ください。
長文読解
【問題】
以下の文章を読んで問いに答えなさい。
そもそも企業はなぜ解数の事発を持つのであろうか。大きく分けて2つの理由が存在する。【a】1つは、関連事業をはじめとして【 】し、事業領域を拡大することにより成長の機会を得るためである。もう1つは、事業環境の変化によるリスクを分散するためである。【b】
事業範囲が拡大するにつれ、企業は個別事業戦路だけでなく、新たに参入すべき事業の選択や事業間の資源配分、事業を全体としてうまく運営していくための全社戦路を重視せざるをえなくなってくる。
全社戦路の要である事業ポートフォリオを考える際は、3つの要素を勘案するのが効果的とされている。第1は事業の魅力度をどう評価するかという点である。第2は、自社がその事業で競争上の優位性を構築する可能性の評価である。【c】第3は、事業間のシナジーの問題である。すなわち、自社の他の事業との相乗効果がどれだけ期待できるかの評価である。【d】
出典:グロービス経営大学院『MBA マネジメント・ブック』ダイヤモンド社
(1)次の一文を挿入するのに最も適切な場所は、文中の【a】〜【d】のうちどこか。
この2つを合わせて平たく言うと、儲かるのか、勝ち目はあるのかということである。
(2)文中の【 】に入れるべき言葉として最も適切なものは次のうちどれか。1つ選びなさい。
- 細分化
- 多角化
- 国際化
- 複雑化
(3)文中下線部の「3つの要素」について、次のア・イの正誤を答えなさい。
ア:競合他社よりも自社事業が優位となることができるか判断する。
イ:事業ごとの独立性がリスク軽減につながる。
- アもイも正しい
- アは正しいが、イは誤り
- アは誤りだが、イは正しい
- アもイも誤り
【解答&解説】
(1)c
(2)2
(3)まずアですが、3つの要素の説明の第2としてあげられているのでアは正しいことがわかります。
続いてイですが、3つの要素の説明に独立性がリスク軽減につながるといったことは書かれていないので誤りとなります。
よって答えは2・・・(答)となります。
※「【SPI】言語の長文読解とは?例題で解説!コツは?長文なしはやばい?」もぜひ合わせてご覧ください。
文章完成
【問題】
文中の空欄に入れる語句として最適なものを選択肢1〜4の中から1つ選びなさい。
植物は細菌などの繁殖を抑制するフィトンチッドという化学物質を発散している。その揮発性の香り成分が人間の体にも薬効があることは【 】されている。そのような知識がない時代から、森林に癒しの効果があることは知られていた。この効果は化学物質によるものではないだろう。
- 科学者の間では常識と
- 科学的にも証明
- 物理的に計測
- 多くの人に体感
【答え】
2
言語の問題は以上となります。
いかがでしたか?今回はSPI(WEBテスティング)で出題される問題をご紹介していきました。
先ほどからご紹介している通り、たった3時間の勉強でWEBテスティングが通過してしまう勉強法があります。
これさえあれば限りなく少ない努力で内定に大きく近づきます。
これは私が100回以上ものSPI受検を通して生み出した、どの本にも載っていない超コスパの良い究極の勉強法です。
興味のある人はぜひ以下のボタンからその方法をチェックしてみてください。


